Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Задачи оценки состояния здоровья человека относятся к классу плохоформализуемых задач, часто с нечетко устанавливаемыми границами. В работах [4, 5, 7, 8] было показано, что одним из эффективных подходов к решению таких задач являются диалоговые методы распознавания образов и нечеткая логика принятия решений, ориентированная на классификацию различных состояний биологических объектов, включая человека.

В работах [4, 3, 7, 13] описываются идеи построения нечетких классификаторов с использованием диалоговых методов распознавания образов и, в частности, с использованием метода интерактивного конструирования двумерных классификационных пространств (ИКДКП). Однако в этих работах достаточно полно раскрываются механизмы отображения многомерных данных в двумерные классификационные пространства, а механизмы нечеткой двумерной классификации рассматриваются лишь на уровне общих идей.

В данной работе предлагается один из эффективных методов нечеткой классификации в двумерном отображающем пространстве, ориентированный на задачи оценки функционального состояния и состояния здоровья человека.

Предполагается, что в ходе предварительного анализа данных было получено двумерное классификационное пространство Ф с использованием метода ИКДКП [4, 3, 10, 13] с отображением в него объектов обучающей выборки альтернативных классов ω_ℓ и ω_r.

С учетом выбранных исходных условий предлагаемый метод реализуется следующей последовательностью действий.

1. Если на предварительном этапе анализа и синтеза метода ИКДКП построено отображающее пространство, то отобранной группе экспертов предлагается оценить пригодность пространства информативных признаков для решения поставленных задач и по шкале от трех до единицы оценить меру доверия к заданной системе признаков. По результатам работы экспертов производится оценка согласованности их действий по коэффициенту конкардации W. В случае достаточной согласованности (W ≥ 0,8) работа экспертов по синтезу нечетных моделей в двумерном классификационном пространстве продолжается. В противном случае состав экспертной группы корректируется до получения W ≥ 0,8 при сохранении требуемого количества эктертов. В соответствии с рекомендациями, принятыми в квалиметрии, количество экспертов для решения выбраного класса задач не должно быть меньше 7. При допуске экспертной группы к дальнейшей работе пространство иформативных признаков может быть скорректировано с выбором новой оценки меры доверия к информативным признакам МДП и к обучающей выборке МДО. После этой процедуры производится повторный синтез двумерного отображающего пространства методом ИКДКП с оставлением лучшего (нового или старого) результатов.

2. Если предварительного двумерного классификационного пространства построено не было, то выбранной группе экспертов предлагается сформировать пространство информативных признаков и оценить меру доверия к нему и возврат к п. 1.

3. Наблюдая результаты отображения объектов обучающей выборки в двумерное пространство Ф, эксперты принимают решение о целесообразности работы с этим типом решающих правил. В случае принятия положительного решения по дальнейшей работе в двумерном пространстве Ф процедура синтеза продолжается, в противном случае принимается решение о выборе других типов решающих правил или об окончании процесса синтеза.

4. Эксперты под руководством инженера- когнитолога изучают свойства отображающих функций, формирующих пространство Ф:

Ф = Y1×Y2, (1)

где Y1 = φ1(A, X); Y2 = φ2(B, X); φ1 и φ2 – функции связи координат многомерного пространства признаков X = x1, x2,…, xn; с координатами двумерного пространства Y1, Y2; n – размерность пространства информативных признаков; A = a1, a2, ..., an; B = b1, b2, ..., bn – вектора настраиваемых (в ходе обучения) параметров.

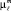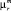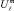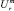5. На экспертном уровне определяется максимальная уверенность в классификации в двумерном пространстве Ф, которая выражается через максимальные величины функций принадлежности и (в терминологии Л. Заде) или через максимальные значения принадлежности к исследуемым классам состояний и в терминологии Е. Шортлифа (ℓ, r – идентификаторы альтернативных классов).

При максимальном доверии экспертов к обучающим выборкам

.

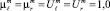C учетом мер доверия МДП и МДО

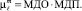(2)

Если у экспертов есть мнение о величине меры недоверия к применяемому методу классификация МНДК, то

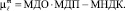(3)

В общем виде 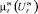и 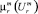для различных классов ω_ℓ и ω_r могут быть различны.

6. Определяются границы областей классов ω_ℓ и ω_r c максимальным уровнем доверия к принимаемым решениям.

При этом следует иметь в виду, или в силу ограничений на объем обучающих выборок реальные границы классов в исходном и отображающем пространстве несколько шире, чем те, что наблюдают эксперты на этапе обучения. Недоучет этого факта будет приводить к снижению качества классификации при решении реальных задач.

Опыт решения практических задач нечеткой классификации в двумерных отображающих пространствах позволил сформировать ряд рекомендаций по выбору областей с 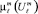и .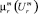

6.1. Зону области пересечения классов ωℓ и ωr рекомендуется увеличить (пунктир на рис. 1) исходя из собственного опыта экспертов и(или) на величины ΔdПℓ и ΔdПr пропорциональные средним расстояниям отображений объектов обучающих выборок класса ωℓ – 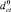и ωr – ( ).

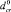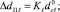
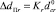Коэффициенты пропорциональности Kℓ и Kr рекомендуется выбирать в диапазоне 1, …, 4 с учетом предпочтений в преобладании ошибок первого и (или) второго рода. Расширенная зона пересечения классов (РЗПК) в Ф исключается из областей максимального доверия к классификации. Удобно при этом расширенные границы зоны пересечения рассматривать как продолжение границ классов ωℓ и ωr вне зоны их пересечения.

6.2. Контуры 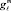и 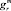областей максимального доверия проводятся экспертами, исходя из специфики решаемой задачи, относительно наблюдаемых границ обучающих выборок и «расширенных» границ областей пересечения. При этом уверенность на границе, обозначенной в предыдущем пункте, определяется как константа aℓ(ar) 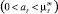(например aℓ = 0,5), и относительно нее строится система линий с равной степенью уверенности в ωℓ(ωr), которая растет по мере приближения к отображению «центра» класса ωℓ(ωr) (рис. 2, а для класса ωℓ). Можно также использовать механизмы обозначения различных плотностей отображений объектов («густота» точки обучающей выборки, числа, оценивающие плотность, цвет) (рис. 2, б) и область, имеющую наибольшую равномерную плотность, определить как ОМД.

6.3. В многомерном пространстве признаков выделяются группы объектов, не пересекающихся с альтернативными классами, но попадающими в зону пересечения в отображающем пространстве. Если такие группы обнаруживаются, то осуществляется их перевод в Ф в область надежной классификации.

Для решения этой задачи в отображаемом пространстве выделяются объекты, сформировавшие зону пересечения классов РЗПК (заштрихованная область на рис. 1). По координатам точек РЗПК восстанавливаются их многомерные координаты с образованием двух подмассивов по классам ωℓ и ωr соответственно. Из объектов обучающих подмассивов класса ωℓ определяется наиболее удаленный от объектов класса ωr. Если это расстояние dkℓ > Kℓdcr (dcr – среднее расстояние между объектами классов ωℓ в многомерном пространстве признаков; Kℓ – коэффициент пропорциональности аналогичный П. 6.2), то принимается гипотеза о существовании группы объектов многомерного пространства с надежной классификацией в РЗПК.

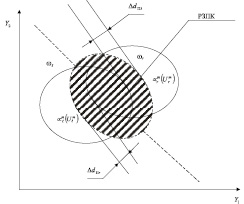
Рис. 1. Формирование расширенной «зоны наложения классов в Ф»

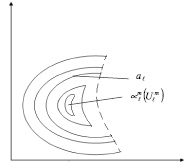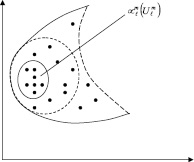 а   б

Рис. 2. Варианты выбора областей максимального доверия: а – по линиям равной уверенности; б – по плотности объектов отображения

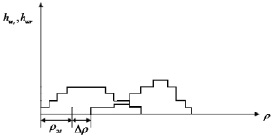
Рис. 3. Гистограммы классов ωr и ωℓ для объектов, формирующих РЗПК

Рассмотрим подробнее вариант выделения группы объектов из ωℓ, не пересекающихся с объектами класса ωr c переводом его в зону надежной классификации.

6.3.1. Определяются координаты С = (c1, c2, ..., cn) центра линии, соединяющей наиболее удаленные многомерные объекты классов ωℓ и ωr из обучающих подмассивов. Относительно этой точки создается шкала типа

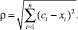(4)

6.3.2. Шкала ρ используется для построения дистальных гистограмм распределения классов ωℓ и ωr для объектов сформировавших РЗПК (рис. 3).

6.3.3. На шкале ρ отмечается радиус эталонной гиперсферы ρЭS такой, чтобы она гарантированно не «захватывала» объекты чужого класса (радиус гиперсферы ρ находился от края альтернативной гистограммы не ближе, чем величина ).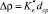

Объект многомерного пространства попадает в эталонную гиперсферу при выполнении условия

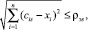(5)

где s – номер эталонной гиперсферы.

6.3.4. Все объекты класса ωℓ, формирующие РЗПК и удовлетворяющие условию (5), из обучающих подмассивов исключаются, а процесс выделения искомых групп класса ωℓ продолжается, пока выполняется условие dkℓ > Kℓdcr. В случае, когда условие не выполняется, считается, что объекты подмассивов классов ωℓ и ωr пересекаются в исходном пространстве признаков.

6.3.5. После нахождения всех эталонных гиперсфер типа (5) для каждой из них определяются многомерные объекты класса ωℓ, наиболее близкие к координатам СS = (с1S, … сiS, …, сnS). Для каждого эталона фиксируются координаты найденных многомерных объектов Y1S и Y2S.

6.3.6. Процедура классификации заключается в том, что если неизвестные объекты принадлежат к эталону с номером s, то они отображаются в точки с координатами Y1 = Y1S и Y2 = Y2S.

Для формирования эталонов типа (5) могут быть использованы гиперпараллелепипеды, механизм получения которых был описан в работах [7, 8].

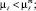
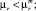
6.4. Осуществляется формирование двумерных областей, для которых 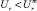и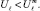

Частично этот механизм описан в пункте 6.2. Для РЗПК после исключения из нее надежно классифицируемых структур ориентиром является формирование площадей с «примерно одинаковым» отношением (для класса ωℓ) и 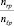(для класса ωr), где nℓq, nrq, nrp и nℓp количество объектов классов ωℓ и ωr на элементах площадей с номерами q и p.

Используя механизм синтеза классификационного пространства, описанный в данной работе, решались задачи ранней и дифференциальной диагностики вибрационной болезни, профессиональных заболеваний работников пылевых профессий, и оценки таких функциональных состояний человека, как оперативный покой, активация психоэмоциональное напряжение и утомление [1, 2, 10, 11]. Исходной информацией для классификации и оценки уровня исследуемых функциональных состояний являлись показатели, характеризующие зрительное внимание человека, регистрируемые аппаратурой, описание которой приведено в работе [12]. Во всех решаемых задачах обеспечивалась диагностическая эффективность не менее 0,9.

Рецензенты:

Бурмака А.А., д.т.н., профессор, главный научный сотрудник НИЦ, ФГУП «18 ЦНИИ» МО РФ, г. Курск;

Серегин С.П., д.м.н., доцент, профессор кафедры биомедицинской инженерии, Юго-Западный государственный университет, г. Курск.