На сегодняшний день одной из существенных проблем во многих отраслях промышленности и на транспорте является проблема вибрации. Вибрационные колебания оказывают негативное влияние на работоспособность транспортных средств, окружающую среду и человека, который находится в зоне вибрационного воздействия. В связи с этим органами государственного и общественного надзора вводятся нормы допустимых значений (уровней) вибраций, которые реализуются в виде государственных стандартов, строительных норм и правил, стандартов предприятий и т д.
На данный момент применяют множество методик и способов защиты от вибрации с применением амортизаторов, динамических гасителей колебаний, динамического уравновешивания двигателей, активных виброзащитных систем и т.д. Наиболее перспективным методом снижения уровней вибрации следует считать применение виброизолирующих устройств с плавающим участком нулевой жесткости [6]. Научными коллективами разработаны виброизоляторы на основе гидравлического, пневматического компенсаторов жесткости, механических корректоров различных конструкций (нелинейный профиль, с призматическими ножами), однако вышеперечисленные устройства не полностью отвечают требованиям виброизоляции, имеют силы вязкого и сухого трения, дополнительные силы инерции. Наиболее эффективным из существующих следует считать виброизолятор на основе электромагнитного компенсатора жесткости [1, 2]. В научной работе итоговой целью является разработка виброизолирующего устройства с корректором жесткости на основе неодимовых магнитов. В [4] представлена конструкция предлагаемого виброизолятора с супермагнитным компенсатором жесткости. Такой компенсатор жесткости на основе неодимовых магнитов наиболее эффективен, так как он наиболее полно отвечает требованиям идеальной виброизоляции как при постоянных по величине, так и при произвольно меняющихся нагрузках.
Результаты исследования и их обсуждение
В [4, 3, 5, 8] представлена конструкция и приведено математическое описание силовых характеристик виброизолятора с супермагнитным компенсатором жесткости. Магнитный компенсатор жесткости подключен параллельно упругому элементу, закрепленному при помощи дюралюминиевых оснований, между вибрирующим и защищаемым основаниями. Магнитный компенсатор представляет из себя два диска, один из которых жестко закреплен на вибрирующем основании через дюралюминиевую стойку, другой диск закреплен на вибрирующем основании при помощи неметаллических стоек. Шток жестко связан с защищаемым объектом. Неодимовые магниты расположены на нижнем и верхнем дисках в отверстиях, а также на обеих сторонах якоря, образуя тем самым компенсатор жесткости с падающей силовой характеристикой. При включении такого компенсатора параллельно упругому элементу, имеющему положительный коэффициент жёсткости, можно получить любую желаемую жёсткость виброизолирующего устройства. Характеристика компенсатора нелинейна, ее вид показан на рис. 1.
При использовании в виброизолирующих устройствах нелинейных компенсаторов исследование их свойств следует осуществлять с использованием методов анализа нелинейных систем. Наиболее удобным является метод гармонической линеаризации нелинейностей (метод гармонического баланса), позволяющий представить нелинейности в колебательных режимах в виде линеаризованных звеньев.
На основе математического описания [1] представлена структурная схема виброизолирующей подвески, содержащей линейный упругий элемент и параллельный ему нелинейный компенсатор жёсткости. Для однозначной нелинейности достаточно определить один коэффициент гармонической линеаризации [7]. В предположении, что на вход нелинейности подаётся гармоническое воздействие x = a·sinωt, этот коэффициент определится как
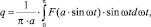 (1)
(1)
где F – уравнение силовой характеристики компенсатора.
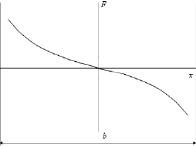
Рис. 1. Тяговая характеристика супермагнитного компенсатора жесткости
Тяговую характеристику нелинейного компенсатора, показанную на рис. 1, можно описать более простым полиномом нечетной степени:
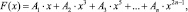 (2)
(2)
где A1, A2, A3, ..., An – произвольные постоянные.
Полином нечетной степени (2) учитывает наклон силовой характеристики, а также конструктивные свойства самого компенсатора, учет разных составляющих полинома позволяет получить желаемую жесткость компенсатора, как представлено на рис. 2.
Выражение (1) при подстановке уравнения (2) будет иметь вид
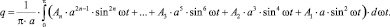 (3)
(3)
При вычислении (3) получим выражение коэффициента гармонической линеаризации компенсатора:
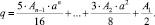 (4)
(4)
Произвольные постоянные A1, A2, A3, ..., An можем определить, составив систему из n-го количества уравнений:
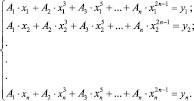 (5)
(5)
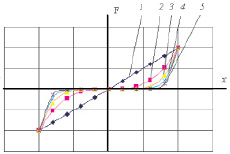
Рис. 2. Силовые характеристики компенсатора жесткости
Решив систему уравнений (5), можем получить необходимые произвольные постоянные A1, A2, A3, ..., An и вычислить коэффициент гармонической линеаризации нелинейного компенсатора жесткости для представления в структурных схемах виброизолирующих устройств с компенсаторами жесткости.
При описании силовой характеристики супермагнитного компенсатора жесткости необходимо учитывать жесткость и свойства корректора, которые можно описать при помощи полинома n-й степени. При различных составляющих полинома можно получить любую жесткость характеристики. Для представления характеристики в системах автоматического управления в работе получен коэффициент гармонической линеаризации для полинома n-й степени.
Работа выполнена при поддержке стипендии Президента Российской Федерации для молодых ученых, приказ Министерства образования и науки РФ № 184 от 10 марта 2015 года.
Рецензенты:
Темлякова З.С., д.т.н., профессор кафедры электромеханики, Новосибирский государственный технический университет, г. Новосибирск;
Щуров Н.И., д.т.н., профессор, заведующий кафедрой электротехнических комплексов, Новосибирский государственный технический университет, г. Новосибирск.



