Передаваемые по физическому каналу данные в процессе передачи под воздействием помех могут исказиться. Для обнаружения и исправления возникающих ошибок без необходимости повторной передачи искаженных данных используют помехоустойчивое кодирование.
На сегодняшний день в теории кодирования известен ряд методов помехоустойчивого кодирования/декодирования, различающихся корректирующей способностью, сложностью реализации и рядом других параметров [2, 7, 8, 9]. Одним из лучших по соотношению эффективности и сложности реализации является метод многопорогового декодирования (МПД) [3, 6].
Для МПД известен алгоритм работы в каналах связи со стираниями, применение которого позволяет существенно увеличить долю исправляемых ошибок (стираний) по сравнению со случаем применения демодулятора, формирующего жесткие решения относительно принятых битов (случай двоичного-симметричного канала связи). Известные результаты исследования эффективности МПД в таком канале [1] показали, что восстановить стертые символы оказывается значительно проще, чем исправлять ошибки.
Отметим, что представленные в [1] результаты теоретически могут быть улучшены как за счет использования лучших кодов, так и за счет применения более сложных каскадных схем кодирования. Например, в качестве внешнего кодека может быть использован кодек кода с контролем по четности (ККЧ), а в качестве внутреннего – кодек МПД. Перечисленные способы повышения эффективности МПД в каналах со стираниями и результаты их исследования в литературе описаны недостаточно полно. Поэтому целью данной статьи является устранение указанного недостатка.
Описание работы МПД в каналах со стираниями
В классической модели канала связи со стираниями каждый бит может быть передан правильно с вероятностью 1 – Pc или стерт с вероятностью Pc.
Работа МПД в канале со стираниями заключается в том, что сначала, как и в двоичном симметричном канале [2], вычисляется синдром:
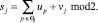(1)
Здесь up – p-й элемент принятого из канала информационного вектора; vj – j-й элемент принятого из канала проверочного вектора; Θj – множество номеров информационных символов, участвующих в формировании j-го проверочного символа. Отметим, что стертые в канале информационные и проверочные символы при вычислении проверки не используются, а их число запоминается в разностном регистре.
Затем в процессе декодирования стертого информационного бита среди относящихся к нему проверок ищется проверка, содержащая только одно стирание (dj = 1). Очевидно, что это стирание будет вызвано декодируемым информационным битом, который по значению символа синдрома в соответствии с (1) может быть легко восстановлен. При этом также необходимо провести коррекцию всех проверок для восстановленного информационного бита и уменьшить на единицу число стираний в разностном регистре для этих же проверок [1].
Для используемых в МПД СОК известна нижняя оценка вероятности невосстановления символа в канале связи со стираниями при использовании ОД, которая равна 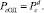[2]
(2)
Для получения этой оценки используется тот факт, что информационный символ точно не будет восстановлен, если он и все проверки, относящиеся к нему, стерты.
На рис. 1 представлены результаты эффективности декодирования МПД для блоковых СОК. Моделирование проводилось для кода длиной n = 16000 бит с кодовой скоростью R = 4/8 при 40 итерациях декодирования и различным минимальным кодовым расстоянием d. На этом рисунке сплошными линиями представлены зависимости вероятности стирания после декодирования Pн (вероятность невосстановления бита) от вероятности стирания Pс в канале связи со стираниями при различных значениях кодового расстояния d. Из рисунка видно, что при увеличении минимального кодового расстояния вероятность невосстановления стирания заметно уменьшается, но область, в которой МПД обеспечивает декодирование близкое к оптимальному (для d = 7 начиная с вероятности 0,46; для d = 9 начиная с вероятности 0,4 и т.д.), смещается в область меньшей вероятности стирания, тем самым удаляясь от пропускной способности канала. Также на данном рисунке представлена кривая «lowEst OD, d = 11», рассчитанная в соответствии с выражением (2), которая позволяет судить о том, что МПД для кода с d = 11 начиная с вероятности 0,37 вплотную приближается к эффективности ОД.
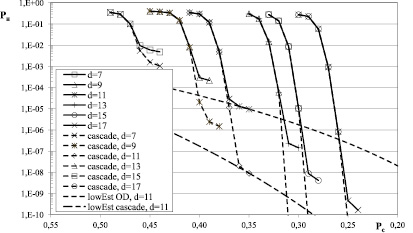
Рис. 1. Характеристики в канале со стираниями для блоковых СОК при различным d
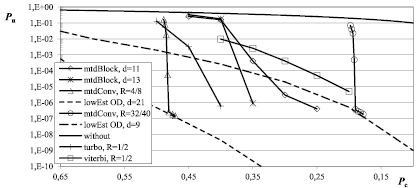
Рис. 2. Характеристики современных методов помехоустойчивого кодирования/декодирования в канале со стираниями
В работе [1] были представлены результаты исследования эффективности МПД для блоковых СОК в каналах связи со стираниями, представленные на рис. 2 кривыми с пометкой «mtdBlock». Длина данных кодов не превосходит 8000 бит, а кодовая скорость R = 5/10 с различным числом минимальных кодовых расстояний d. При получении представленных зависимостей использовались 10 итераций декодирования.
Из данного рисунка видно, что полученные ранее характеристики МПД (кривые с пометкой «mtdBlock») превосходят эффективность практически реализуемого декодера Витерби (кривая «viterbi, R = 1/2, K = 7») и оказываются несколько хуже эффективности декодера турбо кода (кривая «turbo, R = 1/2»). Но при этом сложность практической реализации МПД (количество операций, требующихся для декодирования одного информационного бита) оказывается более чем на порядок меньше сложности декодера турбо кода [4].
В настоящее время результаты были значительно улучшены за счет того, что авторами данной работы были построены новые более длинные и менее чувствительные к размножению ошибок сверточные самоортогональные коды [5]. В частности, на рис. 2 кривыми с пометкой «mtdConv» представлены результаты моделирования для кодов длиной 200000 и 2500000 битов, кодовыми скоростями R = 4/8 и R = 32/40 и минимальными кодовыми расстояниями d = 21 и d = 9 с 50 и 150 итерациями декодирования МПД соответственно.
Представленная на рис. 2 кривая «mtdConv, R = 4/8» позволяет говорить, что с помощью МПД удается обеспечить декодирование, близкое к оптимальному, начиная с вероятности стирания 0,48. Отметим, что пропускная способность используемого стирающего канала равна 0,5, т.е. теоретически в таком канале можно исправлять до 50 % стираний. А кривая «mtdConv, R = 32/40» показывает, что, начиная с вероятности стирания 0,19, МПД обеспечивает декодирование, близкое к оптимальному для используемого сверточного кода. При этом пропускная способность стирающего канала составляет 0,8, т.е. теоретически можно исправлять до 20 % стираний.
Для дополнительного повышения корректирующей способности далее рассмотрим случай использования каскадирования СОК с контролем по четности (ККЧ).
Каскадирование блокового МПД и кода с контролем по четности
Несомненно, что одним из наиболее мощных подходов к повышению ЭВК является применение МПД в составе каскадных кодовых конструкций, поэтому для дополнительного выигрыша кодирования предлагается совместное использование МПД СОК и ККЧ. При использовании каскадирования в качестве внешнего кода будем использовать ККЧ с кодовой скоростью R1, а в качестве внутреннего – МПД со скоростью R2. При этом R1 должна быть как можно ближе к 1 для того, чтобы доля полезной информации (без проверочных символов) оставалась на прежнем уровне.
Для предварительной оценки эффективности предложенной каскадной схемы полезно получить нижнюю оценку невосстановления стирания после декодера ККЧ.
Обычно код с ККЧ с длиной n используется только для обнаружения ошибок, но в данном канале связи он способен исправлять одно стирание. Это возможно, когда на вход декодера ККЧ поступает последовательность, где только один символ стерт, а все остальные не стерты. При этом вероятность невосстановления стирания выражается
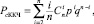(3)
где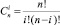 
; p – вероятность стирания; q = 1 – p – вероятность правильного приема. Так как на вход декодера ККЧ символы поступают после МПД, то вероятность стирания p в выражении (3) будет эквивалентна выражению (2).
В итоге можно выразить нижнюю оценку вероятности невосстановления двух и более стираний для предложенной каскадной схемы:
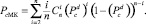(4)
Далее рассмотрим результаты моделирования для описанного случая каскадирования МПД и ККЧ при различных d и n СОК и длине ККЧ равной 50 битам (кривые с пометкой «cascade» на рисунках 1 и 2, соответственно). Также на данных рисунках представлены кривые с пометкой «lowEst cascade», соответствующие нижним оценкам невосстановления стирания, полученные из (4) для каскада при d = 11, которые подтверждают, что МПД способен приблизиться к ним вплотную. Из сравнения рисунков видно, что каскадная схема ведет себя похожим образом при варьировании различных параметров, что и обычный МПД, но при одной и той же вероятности стирания обеспечивает лучшую вероятность исправления на несколько десятичных порядков. В частности, при снижении информативности передаваемых данных на 2 % (длина ККЧ равна 50 бит) при вероятности стирания 0,36 удается повысить корректирующую способность кодека на три десятичных порядка (кривые «d = 11» «cascade, d = 11» на рис. 1).
Выводы
Итак, в ходе данной работы было проведено исследование МПД в каналах связи со стираниями при различных его параметрах (длины кода, минимального кодового расстояния). В процессе исследования получены новые более длинные и менее чувствительные к размножению ошибок самоортогональные коды, а также проведен сравнительный анализ с ранее полученными результатами. Далее была предложена новая каскадная схема использования МПД совместно с кодом контроля по четности в каналах связи со стираниями. Приведены нижние оценки невосстановления стирания предложенной схемы. Проведено исследование характеристик каскада при варьировании параметров кодеков СОК и ККЧ.
Полученные результаты позволяют говорить о том, что МПД способен эффективно работать в каналах связи со стираниями, а при использовании каскадной схемы способен еще на несколько десятичных порядков увеличить свою корректирующую способность, оставаясь при этом таким же легко реализуемым (как программно, так и аппаратно).
Рецензенты:
Еремеев В.В., д.т.н., профессор, директор НИИ «Фотон», ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань;
Костров Б.В., д.т.н., зав. кафедрой ЭВМ, ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.