Традиционный подход цифрового регулирования [5–7] выражается в замене непрерывной континуальной модели регулирования (рис. 1):
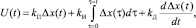 (1)
(1)
её дискретными аналогами на основе преобразования интеграла и производной [2, 4]:
1) по формуле «прямоугольников» (модель П):
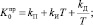
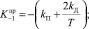
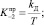 (2)
(2)
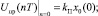 (3)
(3)
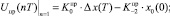 (4)
(4)
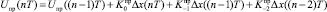 для n ≥ 2; (5)
для n ≥ 2; (5)
2) по формуле «трапеций» (модель Т):
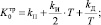
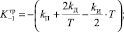
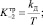 (6)
(6)
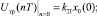 (7)
(7)
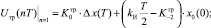 (8)
(8)
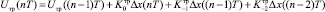 для n ≥ 2. (9)
для n ≥ 2. (9)
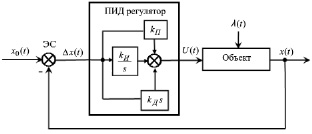
Рис. 1. Структура контура регулирования: x0(t) – задающее воздействие; Δx(t) – рассогласование в текущий момент (отклонение, ошибка, невязка); kП, kИ, kД – настроечные параметры регулятора; U(t) – управляющее воздействие; λ(t) – возмущающее воздействие на объект; x(t) – регулируемая величина; ЭС – элемент сравнения (Δx(t) пропорционален x0(t) – x(t)); t = nT (n – момент времени; T – период опроса датчиков)
3) по формуле «Симпсона» (модель С):
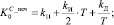
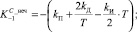
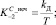 (10)
(10)
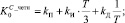
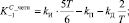
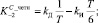 (11)
(11)
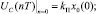 (12)
(12)
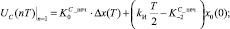 (13)
(13)
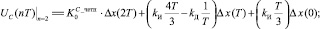 (14)
(14)
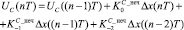 для n = 2k + 1, k = 1, 2, ...; (15)
для n = 2k + 1, k = 1, 2, ...; (15)
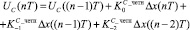 для n = 2k, k = 2, 3, ... (16)
для n = 2k, k = 2, 3, ... (16)
Считалось, что при замене интеграла в континуальной модели (1) формулой Симпсона возникает более точная цифровая модель процесса регулирования, чем при замене интеграла формулой «трапеций» или «прямоугольников», а замена интеграла в (1) формулой «прямоугольников» приводит к менее точной цифровой модели процесса управления.
Однако исследование регуляторов и соответствующих процессов моделирования их функционирования при моделировании приводов постоянного тока как объектов управления показывает, что существует достаточно широкий класс значений настроечных параметров (kП, kИ и kД), при которых модель П имеет существенно лучшие динамические показатели в сравнении с моделями Т и С (рис. 2), а модель T – в сравнении с моделью C (рис. 3). Таким образом, с целью улучшения качества цифрового регулирования очевидна потребность создания и применения модели смешанного регулирования, основная идея которой заключается в поиске минимального рассогласования
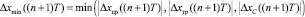
и выборе соответствующего минимальному отклонению Δxmin((n +1)T) управляющего воздействия 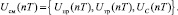
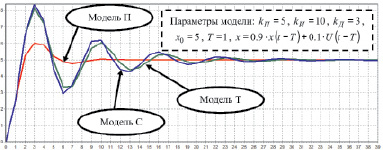
Рис. 2. Моделирование ПИД регулирования [3], показывающее лучшие динамические характеристики модели П в сравнении с моделями Т и С
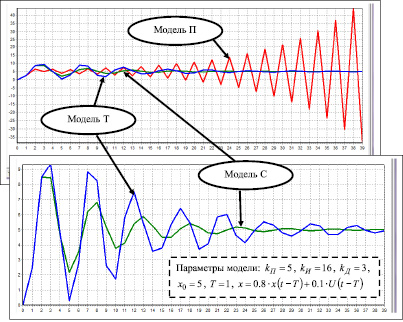
Рис. 3. Моделирование ПИД регулирования [3], показывающее лучшие динамические характеристики модели Т в сравнении с моделями Т и С
Модель смешанного ПИД регулирования (модель Cм):
1. Определение критериев выбора моделей:
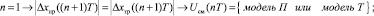 (17)
(17)
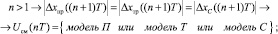 (18)
(18)
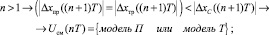 (19)
(19)
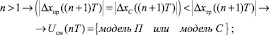 (20)
(20)
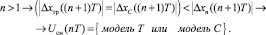 (21)
(21)
2. Для момента времени t = 0 (n = 0):Uсм(0) = kПx0(0).
3. При t = T (n = 1) вычисляются управляющие воздействия Uпр(T) и Uтр(T) по соответствующим формулам, реакция объекта управления xпр(2T) и xтр(2T), рассогласование 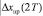 и
и 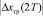 , выбирается модель регулирования (модель П или модель Т), соответствующая минимальному абсолютному значению ошибки:
, выбирается модель регулирования (модель П или модель Т), соответствующая минимальному абсолютному значению ошибки:
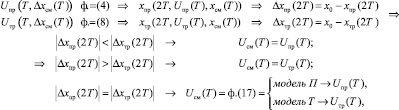
где ф.(*) – вычисление в соответствии с формулой (*).
4. Для момента времени t = 2T (n = 2) вычисляются возможные управляющие воздействия Uпр(2T), Uтр(2T) и UС(2T) по соответствующим формулам, реакция объекта управления xпр(3T), xтр(3T) и xС(3T), рассогласование 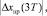
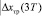 и
и 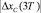 , выбирается модель ПИД регулирования (модель П, модель Т или модель С), соответствующая минимальному абсолютному значению невязки:
, выбирается модель ПИД регулирования (модель П, модель Т или модель С), соответствующая минимальному абсолютному значению невязки:

5. Для t = nT (n = 2k + 1, k = 1, 2, ...) вычисляются Uпр(nT), Uтр(nT) и UС(nT) и, по соответствующим формулам, реакция объекта управления xпр((n +1)T), xтр((n +1)T) и xС((n +1)T), рассогласование 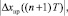
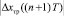 и
и 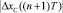 и выбирается модель, соответствующая минимальному абсолютному значению рассогласования:
и выбирается модель, соответствующая минимальному абсолютному значению рассогласования:

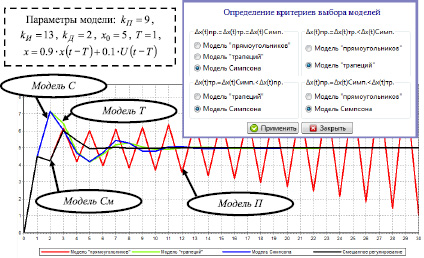
Рис. 4. Моделирование ПИД регулирования [1], показывающее лучшие динамические характеристики модели См в сравнении с моделями П, Т и С
6. Для момента времени t = nT (n = 2k, k = 2, 3, ...) исполнение аналогично пункту 5 с отличием вычисления UC(nT) в соответствии с формулой (16).
Результаты моделирования при
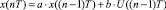
(привод постоянного тока) с использованием созданных программ [1, 3] (рис. 4) показали эффективность предложенной модели.
Основные результаты:
1) построена новая алгоритмическая модель на основе моделей «прямоугольников», «трапеций» и Симпсона, отличающаяся выбором наилучшего управляющего воздействия на каждом шаге;
2) в случае использования математических моделей приводов постоянного тока предложенный алгоритм дает лучшие показатели изменения рассогласования (невязки);
3) результаты исследования предложенного смешанного регулирования позволяют выбрать новый алгоритм в качестве основы создания реальных алгоритмов цифрового ПИД регулирования.
Можно надеяться, что внедрение новой алгоритмической модели приведет к лучшим динамическим характеристикам систем цифрового ПИД регулирования.
Исследование выполнено при поддержке «Госуниверситет-УНПК» по теме «Разработка программной системы поддержки процесса управления в предаварийных состояниях для восстановления нормальной работы», приказ № 7-н/26 от 23.10.2013 г.
Рецензенты:
Раков В.И., д.т.н., профессор кафедры «Информационные системы», ФГБОУ ВПО «Госуниверситет – УНПК», г. Орёл;
Коськин А.В., д.т.н., профессор, проректор по информатизации и спецпроектам, ФГБОУ ВПО «Госуниверситет – УНПК», г. Орёл.



