По сути, композиционные материалы (КМ) представляют собой термодинамические неравновесные системы, состоящие из двух или более компонентов, отличающихся по химическому составу, физико-механическим свойствам и разделенных в материале четко выраженной границей. Каждый из компонентов вводится в состав, чтобы придать ему требуемые свойства, которыми не обладает каждый из компонентов в отдельности. Комбинируя объемное соотношение компонентов, можно получать материалы с требуемыми характеристиками [4, 5].
Цель работы – разработать математическую модель структуры и механических свойств древесного композиционного материала (ДКМ), позволяющую теоретически изучить зависимость прочностных свойств от параметров исходных компонентов, конкретно от концентрации и фракционного состава древесины, технологии получения и внешних воздействий. При построении модели используются в полной мере вычислительные возможности современных компьютеров, а также принципы дискретизации объекта, высокого пространственного разрешения [3].
Структура и механические свойства композиционных материалов чрезвычайно сложны для моделирования из-за необходимости учитывать в модели несколько компонентов и все виды механической связи между ними, форму и взаимное расположение частиц компонентов в материале, распределенную в пространстве внешнюю нагрузку.
Для моделирования структуры и механических свойств древесного композиционного материала используется метод динамики частиц, который в последние десятилетия все чаще используется в различных отраслях науки и техники [1, 2, 3].

Рис. 1. Представление древесного композиционного материала в модели: выделенное темным – древесина; серым – песок; белым – полимер
Для того чтобы модель обладала высоким пространственным разрешением, моделируемый образец ДКМ разбивается на множество (1000–20000) элементов (рис. 1).
Моделирование производится в двумерном пространстве XZ, при этом элементы имеют одинаковую круговую форму с одинаковым диаметром dЭ. Элементы по своим физическим свойствам делятся на три типа (древесина, полимер, песок).
Элементы имеют возможность двигаться в процессе механических испытаний образца по законам классической механики, что приводит к изменению формы и состояния всего образца. В частности, в модели можно воспроизвести различные виды разрушения материала, механические колебания и волны.
Состояние каждого элемента-круга Ei задается четырьмя переменными: декартовыми координатами его центра (xi, zi) и двумя составляющими скорости (vxi, vzi). Механическое взаимодействие элементов между собой принято вязкоупругим, что позволяет заложить в модель основные механические свойства компонентов материала – модуль упругости, коэффициент внутреннего трения, силу адгезии. В модели учитывается, что между соседними элементами могут возникать силы отталкивания (при внедрении элементов друг в друга) или притяжения (при отдалении сцепленных элементов друг от друга) (рис. 2).
В начальный момент времени элементы случайным образом распределяются в области прямоугольной формы. Для того чтобы первоначально нестабильная механическая система пришла в механическое равновесие, в течение 1 секунды модельного времени производится интегрирование уравнений механического движения элементов. В результате этого элементы формируют плотную упаковку. После этого производится разбиение модельного композита на компоненты. В первую очередь выделяются области пространства, представляющие собой древесину.
В зависимости от концентрации и заданного фракционного состава они представляются определенной комбинацией элементов. Затем оставшиеся элементы, в соответствии с заданным составом, разделяются случайным образом на «полимер» и «песок».
Уравнения движения элементов составляются на основе второго закона Ньютона.
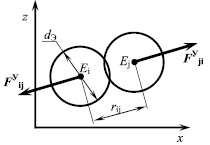
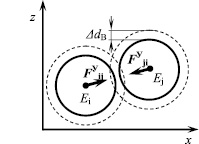
а б
Рис. 2. Контакт сил взаимодействия элементов древесного композиционного материала: а – силы отталкивания при внедрении элементов друг в друга; б – силы притяжения при удалении элементов друг от друга до определенного расстояния
Используемые уравнения представляют собой дифференциальные уравнения второго порядка и решаются в процессе моделирования численным методом – методом Рунге – Кутты второго порядка
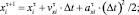
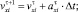
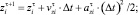
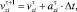 (1)
(1)
где i – номер элемента; τ и τ+1 – индексы текущего и следующего временного шага; Δt – шаг интегрирования по времени; xi, vi, ai – координата, скорость, ускорение элемента.
Данный численный метод имеет второй порядок точности по координате и первый порядок точности по скорости. Метод является универсальным, надежным, а также быстро программируемым. Шаг интегрирования системы дифференциальных уравнений составлял Δt = 0,0001 с.
По общепринятой классификации моделей предлагаемая модель является алгоритмической, но не аналитической. Это означает, что выходные характеристики модели рассчитываются по входным не путем аналитических преобразований (это в принципе невозможно для моделируемого процесса), а с помощью пространственной и временной дискретизации и соответствующего алгоритма расчета. Расчет по приведенным выше формулам является довольно громоздким и включает в себя три цикла, вложенных один в другой: по номеру компьютерного эксперимента, по номеру временного шага и по номеру элемента.
Для решения системы дифференциальных и алгебраических уравнений, которая лежит в основе модели, разработана компьютерная программа для моделирования структуры и механических свойств древесного композиционного материала, которая разработана в среде Borland Delphi 7.0 на языке программирования Object Pascal. Программа предназначена для моделирования механического поведения древесного композиционного материала заданного состава. В процессе работы программа реализует испытание образца на изгиб, непрерывно выводит на экран компьютера изображение образца и изгибающих пуансонов, а также диаграмму напряжение-деформация.
Основные технические характеристики программы: количество элементов композита от 5000 до 20000; ориентировочное время проведения одного компьютерного эксперимента около 5 мин (при тактовой частоте процессора 3 ГГц).
В модели используется целый ряд коэффициентов, связанный с дискретизацией среды (разбиением на отдельные элементы шаровой формы): mЭ, dЭ, c, d. Изложим методику их определения по справочным данным для исходных компонентов.
Расчет массы одного элемента среды (древесины, полимера, или песка) mЭ производится с использованием табличного значения плотности материала и геометрических соображений:
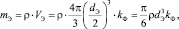 (2)
(2)
где ρ – объемная плотность материала, кг/м3; VЭ – объем элемента, м3; kФ – коэффициент формы, необходимый для учета того, что шарообразные элементы не заполняют пространство полностью (между элементами остаются незаполненные поры), безразмерный. Значение коэффициента kФ зависит от плотности случайной упаковки и принято равным 1,4.
Для расчета жесткости взаимодействия двух элементов используется табличное значение модуля упругости материала и также геометрические соображения, касающиеся дискретизации:
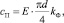 (3)
(3)
где Е – модуль упругости материала, Па.
Коэффициент вязкого трения d связан внутренним трением в рассматриваемой среде и определяется по справочным значениям расстояния затухания звуковых волн в данной среде.
Коэффициент α обнуления взаимодействия между соседними элементами рассчитывается по справочным значениям предельной деформации при испытании образцов материала на растяжение.
Для изучения влияния концентрации древесины сД в древесном композиционном материале проведена серия компьютерных экспериментов, в которой изменяли сД от 0 до 100 % с шагом 10 % при постоянном соотношении концентраций полимера и песка сПл:сПс = 2:1. Обнаружено, что наилучшими механическими свойствами материал обладает при концентрации древесины около 50…55 % (концентрация полимера и песка при этом cПл = 30…33 %, сПс = 17…20 %). С увеличением концентрации древесины от 0 до 55 % увеличиваются σп и εп, то есть увеличивается прочность и уменьшается хрупкость материала за счет армирования композита древесными фрагментами и уменьшения концентрации песка, вызывающего хрупкость. Однако дальнейшее увеличение концентрации древесины (от 55 до 100 %) не целесообразно, так как уменьшается содержание полимера, и его становится недостаточно, чтобы надежно окружить древесные фрагменты и обеспечить прочную связь между ними. При этом материал также становится хрупким и приближается по свойствам к слабо склеенным и слежавшимся опилкам. Кроме того, снижение предела прочности σп происходит из-за уменьшения содержания песка, придающего прочность материалу. Таким образом, в качестве оптимального можно рассматривать состав 50 % древесины + 33 % полимера + 17 % песка.


а б
Рис. 3. Зависимость механических характеристик древесного композиционного материала от концентрации древесины: а – зависимость предела прочности σп; б – зависимость предельной относительной деформации εп
На рис. 3 показана зависимость предела прочности (а) и предельной относительной деформации (б) при испытании на изгиб древесного композиционного материала от концентрации древесины. Необходимо отметить, что данная модификация модели адекватна при концентрациях древесины до 80…85 %, а при больших концентрациях воспроизводит не отдельные слабо связанные между собой фрагменты древесины, а протяженные связанные участки древесины.
В случае сД = 100 % воспроизводится цельный образец древесины с изотропными свойствами. Поэтому для концентрации древесины более 80…85 % необходима была бы доработка модели.
Выводы
Таким образом, на основе математической модели структуры древесного композиционного материала изучено влияние концентрации древесины в составе на прочностные свойства. Оптимальным составом древесного композиционного материала, при котором достигаются приемлемые предел прочности и предельная деформация, является состав 45…50 об. % древесины, 30…35 об. % полимера, 17…22 об. % песка.
Увеличение роста эффективности производства изделий из древесных композиционных материалов может быть достигнуто за счет замены деревянных и железобетонных изделий [6], и это будет способствовать сохранению строевого леса, использованию отходов лесного комплекса и отходов промышленности, оздоровлению экологической обстановки и созданию новых рабочих мест.
Рецензенты:
Афоничев Д.Н., д.т.н., профессор, заведующий кафедрой электротехники и автоматики, ФГБОУ ВПО «Воронежский государственный аграрный университет имени Императора Петра I», г. Воронеж;
Кондрашова Е.В., д.т.н., доцент, профессор кафедры технического сервиса и технологии машиностроения, ФГБОУ ВПО «Воронежский государственный аграрный университет имени Императора Петра I», г. Воронеж.



