Увеличение объема и повышение сложности обрабатываемых данных, структура которых представляет собой символьные последовательности требуют повышения эффективности их обработки и анализа. Задачи нечеткого поиска чаще всего возникают при коррекции ошибок, фильтрации нежелательных сообщений, обнаружении плагиата, поиске с учетом форм одного и того же слова и основаны на определении расстояния между строками. В настоящее время при сравнении геномных последовательностей активно используются алгоритмы поиска неструктурированных данных. Данные алгоритмы могут быть применены при анализе геномов для разрешении проблем репродуктивной системы и развитии персонифицированной медицины при сравнении нуклеотидных последовательностей, так как последовательность нуклеотидов ДНК может быть представлена как последовательность символов, содержащая 4 «буквы» – A, T, G, C, каждая из которых соответствует определенному нуклеотиду.
В настоящее время имеется огромное количество генетических данных, находящихся в открытом доступе на специализированных порталах. Математическая, аналитическая и программная обработка данных последовательностей имеет явное преимущество перед экспериментальными исследованиями в области трудоемкости, стоимости и времени и должна быть широко внедрена для изучения в различные сферы генетики и медицины, в том числе для задач оценки состояния репродуктивной системы.
Релевантность результатов нечеткого поиска зависит от учета искажений символов слов различных типов (вставки, удаления, замены и транспозиции символов), но генетическое строение молекулы ДНК допускает искажения. Ключевым элементом организации нечёткого поиска является выбор меры сходства слов или обратной функции – функции расстояния между словами, часто называемой метрикой. Наибольшее распространение в случае нечеткого поиска подстроки в нуклеотидной строке получили трансформационные метрики (принят термин расстояния редактирования – в области текстового поиска) [2].
Наиболее известными расстояниями редактирования являются расстояния Хэмминга, Левенштейна, а также n-граммы [1, 3, 5].
Расстояние Хэмминга определяется как число позиций, в которых для двух слов одинаковой длины соответствующие символы длины [8]. В [6] приводится альтернативное определение: если две строки Ai и Aj имеют одинаковую длину n, расстояние Хемминга dH (Ai, Aj) определяется как минимальное количество подстановок (замен), необходимых для преобразования строки Ai в строку Aj.
Удовлетворяя следующим условиям, расстояние Хэмминга обладает свойствами метрики:
d(x, y) ≥ 0;
d(x, y) = 0 ⇔ x = y;
d(x, y) = d(y, x);
d(x, z) ≤ d(x, y) + d(y, z).
Расстояние Левенштейна позволяет сравнивать строки различной длины с учетом таких искажений, как замены, вставки, и удаления. Расстояние Левенштейна равно минимальному числу элементарных операций редактирования, необходимых для преобразования одной строки в другую.
В [4] расстояние Левенштейна dL (Ai, Aj) определяется как минимальное количество операций вставки, удаления либо замены одного символа на другой, необходимых для превращения одной строки в другую, а [6] определяет расстояние Левенштейна учитывающим только операции удаления и вставки, а расстояние, учитывающее еще и замену (подстановку), называется расстоянием преобразования dE (Ai, Aj).
Пусть S1 и S2 – две строки (длиной M и N соответственно) над некоторым алфавитом, тогда расстояние dL (S1, S2) можно посчитать по следующей рекуррентной формуле:
dL (S1, S2) = D(M, N),
где
здесь шаг по i символизирует удаление (D) из первой строки, по j – вставку (I) в первую строку, а шаг по обоим индексам символизирует замену символа (R) или отсутствие изменений (M).
Очевидно, справедливы следующие утверждения:
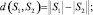
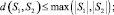
d(S1, S2) = 0 ⇔ S1 = S2.
В модификации расстояния редактирования, предложенной Дамерау [7], в множество элементарных операций включены операции перестановки (транспозиции) двух соседних символов, но при этом требуется, чтобы к транспонированным символам не применялись другие операции редактирования.
Основным недостатком расстояния редактирования Хэмминга является требование одинаковой длины строк, таким образом, расстояние Хэмминга подходит для расчета расстояния редактирования с учетом таких искажений, как замена и транспозиция, но не подходит при вставках и удалениях. Учитывать все названные искажения позволяют расстояния Левенштейна и Дамерау – Левенштейна, но при перестановке местами слов или частей слов получаются сравнительно большие расстояния [5]. Ввиду того что описанные расстояния редактирования не нормированы по длине строк, строки с одинаковым количеством допустимых искажений символов, но различной длины будут иметь одинаковое значение dH расстояния Хэмминга, а значения расстояний Левенштейна dL (Ai, Aj) и Дамерау – Левенштейна dE (Ai, Aj) между совершенно разными короткими словами оказываются меньшими, чем расстояния между очень похожими длинными словами. При необходимости метрику можно нормированием по длине строки: dH/n. Известные меры сходства Джаро [9] и Джаро – Уинклера [10] для сравнения коротких строк – коэффициенты, включающие нормирования.

Существуют различные модификации n-граммных расстояний, основанные на подсчете числа общих подстрок равной длины (n-грамм), n-граммами (q-граммами) называют множество подстрок длины n исходной строки. Оценка расстояния производится на основе подсчета количества различающихся n-грамм данного множества. Обобщением расстояния Левенштейна dw (Ai, Aj) является использование матрицы весовых коэффициентов для замены символа i символом j. Это расстояние будет являться метрикой, только если матрица весовых коэффициентов симметрична [6]. Частным случаем будет вариант, учитывающий вес для каждой из операций, вне зависимости от заменяемого символа.
Задача поиска структурного или функционального элемента (мотива) в последовательности межгенного пространства, сводится к поиску подстроки в строке [1], и, несмотря на то, что размерность алфавита небольшая, равна 4, задача осложняется возможностью вставок, делеций и замен в конкретной ключевой позиции.
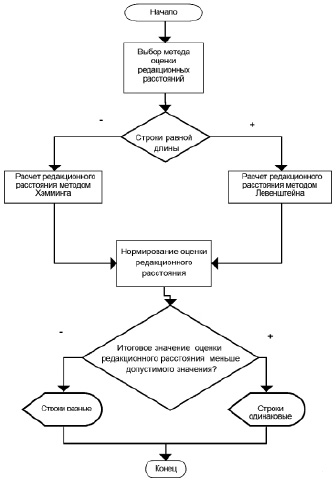
Алгоритм применения расстояний редактирования для задач нечеткого поиска в генетических последовательностях
Например, в последовательности
ctctagtggtcagtgttagcactgcatccagctgactcaggtgggc
необходимо определить наличие следующего мотива:
accactgcactccagcctgag.
Результаты поиска:
ctctagtggtcagtgttagcactgca.tccag.ctgactcaggtgggc
accactgcactccagcctgag.
Сравним найденное и искомое, большими буквами обозначены замены, а точками делеции:
aGcactgca.tccag.ctgaC
accactgcactccagcctgag.
Разработан алгоритм применения расстояний редактирования для задач нечеткого поиска в генетических последовательностях (рисунок). На данный момент для оценки редакционных расстояний может быть использовано 2 метода – Хэмминга и Левенштейна. Для каждого из них есть ряд случаев, когда их рекомендуется применять, например метод Хэмминга не применим к последовательностям разной длины.
Данный алгоритм реализован и модифицирует программу для ЭВМ «Анализ нуклеотидных последовательностей ДНК с помощью точечной матрицы гомологии» при расчете сходства. Программа позволяет выявлять значимые последовательности, а также анализировать последовательности ДНК на предмет наличия прямых и инвертированных повторов заданной степени сходства при проведении визуального анализа генома и целенаправленной идентификации данных секвенирования ДНК с помощью точечной матрицы гомологий для решения задач анализа и оценки состояния репродуктивной системы.
По мере изучения строения ДНК и понимания механизмов и генетического значения вставок, удалений, замены и транспозиции нуклеотидов будут корректироваться алгоритм применения и расчет расстояний редактирования при биоинформационном анализе геномов. В то же время биоинформационные исследования генетических данных уже сейчас позволяют найти особенности и нацелить лабораторные исследования на изучение определенных участков, тем самым сократить время и стоимость исследований в целом.
Работа выполнена в рамках базовой части внутреннего гранта ЮФУ в 2015 году по проекту 213.01–2015/003ВГ «Изучение ДНК-элементов некодирующих белок в структуре различных геномов».
Рецензенты:
Соловьев А.Н., д.ф.-м.н., профессор, заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону;
Елсуков В.С., д.т.н., профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.



