Увеличение объема и повышение сложности обрабатываемых данных, структура которых представляет собой символьные последовательности требуют повышения эффективности их обработки и анализа. Задачи нечеткого поиска чаще всего возникают при коррекции ошибок, фильтрации нежелательных сообщений, обнаружении плагиата, поиске с учетом форм одного и того же слова и основаны на определении расстояния между строками. В настоящее время при сравнении геномных последовательностей активно используются алгоритмы поиска неструктурированных данных. Данные алгоритмы могут быть применены при анализе геномов для разрешении проблем репродуктивной системы и развитии персонифицированной медицины при сравнении нуклеотидных последовательностей, так как последовательность нуклеотидов ДНК может быть представлена как последовательность символов, содержащая 4 «буквы» – A, T, G, C, каждая из которых соответствует определенному нуклеотиду.
В настоящее время имеется огромное количество генетических данных, находящихся в открытом доступе на специализированных порталах. Математическая, аналитическая и программная обработка данных последовательностей имеет явное преимущество перед экспериментальными исследованиями в области трудоемкости, стоимости и времени и должна быть широко внедрена для изучения в различные сферы генетики и медицины, в том числе для задач оценки состояния репродуктивной системы.
Релевантность результатов нечеткого поиска зависит от учета искажений символов слов различных типов (вставки, удаления, замены и транспозиции символов), но генетическое строение молекулы ДНК допускает искажения. Ключевым элементом организации нечёткого поиска является выбор меры сходства слов или обратной функции – функции расстояния между словами, часто называемой метрикой. Наибольшее распространение в случае нечеткого поиска подстроки в нуклеотидной строке получили трансформационные метрики (принят термин расстояния редактирования – в области текстового поиска) [2].
Наиболее известными расстояниями редактирования являются расстояния Хэмминга, Левенштейна, а также n-граммы [1, 3, 5].
Расстояние Хэмминга определяется как число позиций, в которых для двух слов одинаковой длины соответствующие символы длины [8]. В [6] приводится альтернативное определение: если две строки Ai и Aj имеют одинаковую длину n, расстояние Хемминга dH (Ai, Aj) определяется как минимальное количество подстановок (замен), необходимых для преобразования строки Ai в строку Aj.
Удовлетворяя следующим условиям, расстояние Хэмминга обладает свойствами метрики:
d(x, y) ≥ 0;
d(x, y) = 0 ⇔ x = y;
d(x, y) = d(y, x);
d(x, z) ≤ d(x, y) + d(y, z).
Расстояние Левенштейна позволяет сравнивать строки различной длины с учетом таких искажений, как замены, вставки, и удаления. Расстояние Левенштейна равно минимальному числу элементарных операций редактирования, необходимых для преобразования одной строки в другую.
В [4] расстояние Левенштейна dL (Ai, Aj) определяется как минимальное количество операций вставки, удаления либо замены одного символа на другой, необходимых для превращения одной строки в другую, а [6] определяет расстояние Левенштейна учитывающим только операции удаления и вставки, а расстояние, учитывающее еще и замену (подстановку), называется расстоянием преобразования dE (Ai, Aj).
Пусть S1 и S2 – две строки (длиной M и N соответственно) над некоторым алфавитом, тогда расстояние dL (S1, S2) можно посчитать по следующей рекуррентной формуле:
dL (S1, S2) = D(M, N),
где
здесь шаг по i символизирует удаление (D) из первой строки, по j – вставку (I) в первую строку, а шаг по обоим индексам символизирует замену символа (R) или отсутствие изменений (M).
Очевидно, справедливы следующие утверждения:
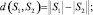
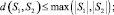
d(S1, S2) = 0 ⇔ S1 = S2.
В модификации расстояния редактирования, предложенной Дамерау [7], в множество элементарных операций включены операции перестановки (транспозиции) двух соседних символов, но при этом требуется, чтобы к транспонированным символам не применялись другие операции редактирования.
Основным недостатком расстояния редактирования Хэмминга является требование одинаковой длины строк, таким образом, расстояние Хэмминга подходит для расчета расстояния редактирования с учетом таких искажений, как замена и транспозиция, но не подходит при вставках и удалениях. Учитывать все названные искажения позволяют расстояния Левенштейна и Дамерау – Левенштейна, но при перестановке местами слов или частей слов получаются сравнительно большие расстояния [5]. Ввиду того что описанные расстояния редактирования не нормированы по длине строк, строки с одинаковым количеством допустимых искажений символов, но различной длины будут иметь одинаковое значение dH расстояния Хэмминга, а значения расстояний Левенштейна dL (Ai, Aj) и Дамерау – Левенштейна dE (Ai, Aj) между совершенно разными короткими словами оказываются меньшими, чем расстояния между очень похожими длинными словами. При необходимости метрику можно нормированием по длине строки: dH/n. Известные меры сходства Джаро [9] и Джаро – Уинклера [10] для сравнения коротких строк – коэффициенты, включающие нормирования.

Существуют различные модификации n-граммных расстояний, основанные на подсчете числа общих подстрок равной длины (n-грамм), n-граммами (q-граммами) называют множество подстрок длины n исходной строки. Оценка расстояния производится на основе подсчета количества различающихся n-грамм данного множества. Обобщением расстояния Левенштейна dw (Ai, Aj) является использование матрицы весовых коэффициентов для замены символа i символом j. Это расстояние будет являться метрикой, только если матрица весовых коэффициентов симметрична [6]. Частным случаем будет вариант, учитывающий вес для каждой из операций, вне зависимости от заменяемого символа.
Задача поиска структурного или функционального элемента (мотива) в последовательности межгенного пространства, сводится к поиску подстроки в строке [1], и, несмотря на то, что размерность алфавита небольшая, равна 4, задача осложняется возможностью вставок, делеций и замен в конкретной ключевой позиции.
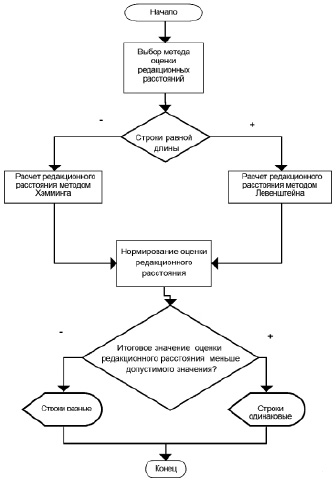
Алгоритм применения расстояний редактирования для задач нечеткого поиска в генетических последовательностях
Например, в последовательности
ctctagtggtcagtgttagcactgcatccagctgactcaggtgggc
необходимо определить наличие следующего мотива:
accactgcactccagcctgag.
Результаты поиска:
ctctagtggtcagtgttagcactgca.tccag.ctgactcaggtgggc
accactgcactccagcctgag.
Сравним найденное и искомое, большими буквами обозначены замены, а точками делеции:
aGcactgca.tccag.ctgaC
accactgcactccagcctgag.
Разработан алгоритм применения расстояний редактирования для задач нечеткого поиска в генетических последовательностях (рисунок). На данный момент для оценки редакционных расстояний может быть использовано 2 метода – Хэмминга и Левенштейна. Для каждого из них есть ряд случаев, когда их рекомендуется применять, например метод Хэмминга не применим к последовательностям разной длины.
Данный алгоритм реализован и модифицирует программу для ЭВМ «Анализ нуклеотидных последовательностей ДНК с помощью точечной матрицы гомологии» при расчете сходства. Программа позволяет выявлять значимые последовательности, а также анализировать последовательности ДНК на предмет наличия прямых и инвертированных повторов заданной степени сходства при проведении визуального анализа генома и целенаправленной идентификации данных секвенирования ДНК с помощью точечной матрицы гомологий для решения задач анализа и оценки состояния репродуктивной системы.
По мере изучения строения ДНК и понимания механизмов и генетического значения вставок, удалений, замены и транспозиции нуклеотидов будут корректироваться алгоритм применения и расчет расстояний редактирования при биоинформационном анализе геномов. В то же время биоинформационные исследования генетических данных уже сейчас позволяют найти особенности и нацелить лабораторные исследования на изучение определенных участков, тем самым сократить время и стоимость исследований в целом.
Работа выполнена в рамках базовой части внутреннего гранта ЮФУ в 2015 году по проекту 213.01–2015/003ВГ «Изучение ДНК-элементов некодирующих белок в структуре различных геномов».
Рецензенты:
Соловьев А.Н., д.ф.-м.н., профессор, заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону;
Елсуков В.С., д.т.н., профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.
Библиографическая ссылка
Пономарева Н.С., Реброва Г.Н., Колина Е.А. ПРИМЕНЕНИЕ РАССТОЯНИЙ РЕДАКТИРОВАНИЯ ПРИ БИОИНФОРМАЦИОННОМ АНАЛИЗЕ ГЕНОМОВ ДЛЯ ЗАДАЧ ОЦЕНКИ СОСТОЯНИЯ РЕПРОДУКТИВНОЙ СИСТЕМЫ // Фундаментальные исследования. 2015. № 7-4. С. 774-777;URL: https://fundamental-research.ru/ru/article/view?id=38819 (дата обращения: 22.12.2025).



