Гидродинамическая теория смазки широко применяется для расчета и конструирования подшипников скольжения с жидкой смазкой, которые являются важными конструктивными элементами разнообразных механизмов и машин. Существует большое количество публикаций, посвященных этой теме, например [5, 3, 8]. Роль упругих деформаций становится очень важной для тяжело нагруженных цилиндрических подшипников скольжения. Поэтому возникла необходимость учета упругих деформаций рабочих поверхностей в гидродинамической теории смазки. Это привело к развитию так называемой упруго-гидродинамической теории, в которой согласованно рассматривались течение смазочного слоя и деформация поверхности контакта, вызванная повышенным давлением в смазочном слое [4]. В этой теории важное место отводится проблеме определения связи между распределением давления в слое и деформацией поверхности.
Основными элементами конструкции гидродинамического подшипника скольжения являются цилиндрический вал, смазочный слой, вкладыш и корпус. Обычно вкладыш подшипника изготавливается из более податливого материала по сравнению с корпусом, который имеет высокую твердость и мало деформируется. По этой причине деформациями корпуса часто пренебрегают и учитывают только деформации вкладыша [1]. При таком упрощенном подходе деформации тонкого вкладыша, ограниченные жестким корпусом, определяются малым параметром – отношением толщины вкладыша к радиусу кривизны. Как показано в монографии [1], в первом приближении по этому малому параметру деформации вкладыша пропорциональны локальному значению давления. Коэффициент пропорциональности называют податливостью вкладыша. Данное приближение связано с известной гипотезой Винклера. В общем случае необходимо учитывать не только деформации вкладыша, но также и деформации корпуса, имеющего конечную жесткость. В таком случае расчеты поверхностных деформаций должны выполняться самосогласованно с вычислениями распределения давления вдоль всего смазочного слоя. Для этой цели необходимо определить общую функциональную связь между поверхностными деформациями и распределением давления в слое смазки, принимая во внимание различие свойств материала вкладыша и корпуса подшипника. Главной целью данной работы является разработка метода установления обобщенного функционального уравнения и применение его для получения решения упруго-гидродинамической контактной задачи.
Постановка задачи
Для описания предлагаемого подхода рассмотрим цилиндрический подшипник скольжения, в котором смазочный слой разделяет стальной вал и бронзовый вкладыш, граничащий со стальным корпусом, как показано на рис. 1. Здесь ω – угловая скорость вращения вала, φ – азимутальный угол, отсчитываемый в направлении часовой стрелки от точки максимального зазора, η и R0 – эксцентриситет и радиус цилиндрического вала, R1 – внутренний радиус вкладыша, R2 и R3 – внутренний и внешний радиусы цилиндрического корпуса, L – длина подшипника. В расчетах используем нулевые граничные условия для деформаций на заданной внешней границе корпуса подшипника. Между валом и вкладышем располагается тонкий слой жидкой смазки, называемый смазочным слоем. Также ставим нулевые граничные условия для давления на торцах подшипника.
Распределение давления в смазочном слое определяется из решения известного уравнения Рейнольдса [3]:
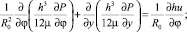(1)
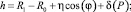
P > 0;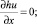 
P ≤ 0. (2)
Здесь h – толщина смазочного слоя; μ – коэффициент вязкости; u – средняя скорость поверхностей вала и вкладыша; y – координата вдоль оси цилиндрического подшипника; φ – азимутальный угол; δ – радиальный прогиб поверхности вкладыша, зависящий от давления в смазочном слое. Метод численного решения уравнения (1) описан в работе [2].
Результаты вычислений
Для иллюстрации метода введем конкретные параметры подшипника скольжения: R1 = 0,03 м, R2 = 0,035 м, R3 = 0,1 м, d = 0,00013 м, E1 = 2,1∙1011 Па, E2 = 1,08∙1011 Па, m1 = 0,3, m2 = 0,34, μ = 0,024 Па/с, ω = 314,16 с–1, где E1 и E2 – модули упругости стального корпуса и бронзового вкладыша; m1 и m2 – коэффициенты Пуассона для материалов корпуса и вкладыша соответственно. Длина и диаметр подшипника предполагаются равными друг другу.
Зависимость упругих деформаций от распределения давления может быть записана в следующей интегральной форме:
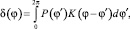(3)
Рис. 1. Геометрическая схема подшипника скольжения: 1 – вал, 2 – бронзовый вкладыш, 3 – корпус
где δ и P – прогиб поверхности и давление, зависящие от азимутального угла. Функцию K(φ – φ′), являющуюся ядром линейного функционала, будем называть функцией податливости. Эта функция не зависит от конкретного распределения давления, но зависит от геометрических характеристик подшипника скольжения. Она может быть найдена на основе численных результатов, описанных в [2]. Для этой цели применяем разложение Фурье:
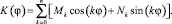(4)
Умножая уравнение (4) на гармонические функции и интегрируя по углу в интервале от 0 до 2π, получаем систему линейных алгебраических уравнений относительно искомых коэффициентов Фурье Mk и Nk [2]. Используя известное распределение давления в смазочном слое и деформации поверхности, рассчитанные пакетом ANSYS, находим коэффициенты Фурье:
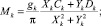
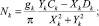
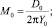k = 1, 2, 3… (5)
где
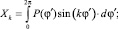
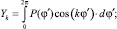
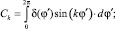
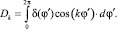(6)
Здесь давление и прогиб поверхности являются функциями угла, которые определяются методом сплайновой интерполяции дискретных узловых значений Pi and δi.
В этой формуле точность результата зависит от выбора верхнего предела суммирования n. В частности, значение n = 10 вполне достаточно для хорошей точности аппроксимации. В связи с применением формулы (4) следует обратить внимание на заметное влияние мелкомасштабных шумовых погрешностей, присутствующих в численных данных, полученных в результате расчетов. Для удаления связанных с таким шумом эффектов можно воспользоваться одним из способов регуляризации [6, 7]. Для подавления паразитных осцилляций вводим множители вида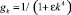 
для Фурье коэффициентов. Здесь ε является малым параметром, который существенно влияет на затухание шумовых осцилляций.
На рис. 2 сплошной линией показана функция (4), соответствующая значению ε = 0,0001. На том же рисунке штриховой линией показана аналитическая аппроксимация, заданная простой формулой вида
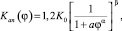(7)
где a = 5; α = 1,7; β = 1,4;
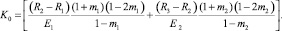(8)
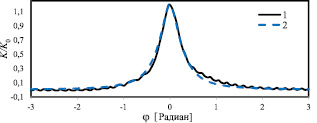
Рис. 2. Функция податливости, полученная из численного решения (кривая 1), в сравнении с аналитической аппроксимацией (кривая 2), заданной формулой (7)
Полученные функции (4) и (7) определяют матрицу податливости для любого распределения давления вдоль смазочного слоя для заданных геометрических параметров подшипника скольжения.
Трехмерные расчеты ANSYS
Далее анализируем различие между матрицами податливости для различных поперечных сечений подшипника скольжения. Используя конечно-разностную схему, описанную в работе [2], вычисляем гидродинамическое давление в смазочном слое для подшипника скольжения конечной длины. На рис. 3 показаны профили давления, соответствующие различным поперечным сечениям (y = const) подшипника. Для определения деформаций, связанных с распределением давления, применяем трехмерный пакет ANSYS. Используя результаты вычислений ANSYS, находим деформации поверхности вкладыша в каждом поперечном сечении и сравниваем трехмерное решение ANSYS в центральном поперечном сечении с двумерным решением. Оба решения представлены на рис. 4. Анализ показывает, что деформация поверхности подшипника в двухмерной расчетной модели ANSYS заметно больше, чем в трехмерной модели. Различие составляет 28 %. Далее сравниваем поведение функций податливости для различных поперечных сечений. Для получения этих функций применяем описанное выше разложение Фурье для различных поперечных сечений подшипника. Расчеты показывают, что функции податливости располагаются довольно близко друг к другу для всех сечений (кроме самых крайних). Поэтому практически можно использовать матрицу податливости, рассчитанную только для центрального сечения.
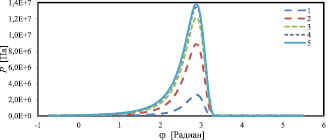
Рис. 3. Азимутальные распределения давления, соответствующие различным поперечным сечениям подшипника скольжения. Кривая 1 – для сечения, близкого к краю подшипника: y = 0,02666 м. Кривые 2, 3, 4, и 5 соответствуют поперечным сечениям y = 0,01999 м, y = 0,01333 м, y = 0,00666 м и y = 0 соответственно
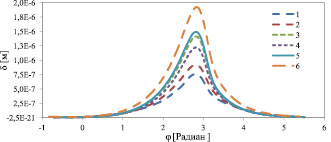
Рис. 4. Деформации поверхности подшипника для различных поперечных сечений (трехмерная модель), а также для двухмерной модели. Кривые 1, 2, 3, 4 и 5 соответствуют прогибу поверхности, полученному по трехмерной модели ANSYS для сечений y = 0,03 м, y = 0,02333 м, y = 0,01666 м, y = 0,00999 м и y = 0,00333 м соответственно; кривая 6 соответствует двухмерной модели ANSYS
Заключение
Предложен эффективный подход, позволяющий вычислить матрицу податливости на основе предварительного расчета давления в смазочном слое и использования программного пакета ANSYS для определения прогиба поверхности. Даже в случаях длинных подшипников скольжения для вычисления поверхностных деформаций следует предпочесть более реалистичную трехмерную модель пакета ANSYS по сравнению с двухмерной моделью. Сравнение показывает, что двухмерная модель дает существенно завышенные значения прогиба поверхности. Для определения функции податливости, обеспечивающей связь давления и прогиба, применяется разложение Фурье. Для подавления шумовых осцилляций вводятся коррекции коэффициентов Фурье посредством множителей регуляризации, которые обеспечивают сглаживание искомой функции податливости. Оказалось, что найденные функции податливости, относящиеся к различным поперечным сечениям подшипника, мало отличаются друг от друга. Поэтому для экономии вычислений достаточно определить функцию податливости только для центрального сечения подшипника. Важно отметить, что функция податливости, зависящая от конструктивных параметров подшипника, не зависит от распределения давления вдоль смазочного слоя. Поэтому функция податливости, найденная один раз для конкретного подшипника, может использоваться многократно в итерационной схеме совместно с уравнением Рейнольдса для самосогласованного моделирования различных динамических режимов подшипника скольжения.
Работа выполнена при поддержке РФФИ (грант № 15-05-00879).
Рецензенты:
Адрианов А.Л., д.ф.-м.н., профессор кафедры «Летательные аппараты», Сибирский государственный аэрокосмический университет, г. Красноярск;
Меновщиков В.А., д.т.н., профессор, заведующий кафедрой «Технология машиностроения», Красноярский государственный агарный университет, г. Красноярск.