Построение адаптивной системы
В работе [1] исследуются электромеханические объекты, где кратность изменения параметров составляет 5–10. Рассмотренные в [1] алгоритмы адаптации нацелены на проведение подстройки системы управления за краткое время, что важно и при управлении электроэнергетическими ГТУ. Поэтому далее, опираясь на теоретическую базу работы [1], заменим объект управления и рассмотрим полученные результаты.
Движение ГТУ с учетом нестабильности свойств запишем в виде
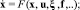 x(t0) = x0, (1)
x(t0) = x0, (1)
где x = x(t) – n-мерная функция состояния системы; u = u(t) – m-мерная функция управляющих воздействий; ξ – вектор ограниченной размерности меняющихся параметров; f = f(t) – n-мерная функция внешних возмущений; х0 – начальное состояние.
Перейдем к описанию нелинейной нестационарной модели ГТУ в виде
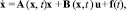 (2)
(2)
где 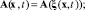
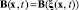 – функциональные матрицы соответствующих размеров. Здесь предполагается управляемость пары (А, В).
– функциональные матрицы соответствующих размеров. Здесь предполагается управляемость пары (А, В).
Выделим в правой части (2) линейную стационарную часть
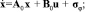 y = Cx, (3)
y = Cx, (3)
где у – p-вектор выходов объекта; 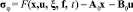 ; u – m-мерный вектор управляющих сигналов: u = (GT), где GT – расход топлива ГТУ (кг/ч); А0, В0, С – соответственно (n×n), (n×m), (p×n)-мерные постоянные матрицы, характеризующие линейную стационарную часть, которая может быть приближением, полученным линеаризацией и усреднением во времени элементов матриц, либо обозначать желаемое поведение объекта, x – вектор состояния
; u – m-мерный вектор управляющих сигналов: u = (GT), где GT – расход топлива ГТУ (кг/ч); А0, В0, С – соответственно (n×n), (n×m), (p×n)-мерные постоянные матрицы, характеризующие линейную стационарную часть, которая может быть приближением, полученным линеаризацией и усреднением во времени элементов матриц, либо обозначать желаемое поведение объекта, x – вектор состояния
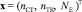 ,
,
где nСТ – частота вращения свободной турбины ГТУ (об/мин); nТК – частота вращения турбокомпрессора ГТУ(об/мин); NE – мощность свободной турбины ГТУ (кВт). Возмущение f = (NG), где NG – мощность нагрузки (кВт). В дальнейших выкладках для упрощения расчетов отнесем NG к состояниям системы. Тогда А0 = Ам, В0 = Вм, Ам – гурвицева матрица (устойчива).
Добавим к (2) уравнение адаптивного регулятора в виде
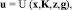 (4)
(4)
где g = g(t)– m-мерный вектор сигналов задания, для ГТУ – это заданная частота вращения свободной турбины nСТзад; К = К(t)– матрица настраиваемых параметров; z = z(t) – m-вектор дополнительных (сигнальных) воздействий. Здесь K и z – средства адаптации: параметрическая настройка (ПН) и сигнальная настройка (СН) [1].
Пусть задана эталонная модель вида
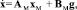 (5)
(5)
где g = (nСТзад). Требуется построить закон управления u(t), выраженный через минимизацию функционала качества на решениях системы (3), (5), такой, что при любых ξ ∈ M, x(t0), xМ(t0) выполнялось неравенство
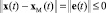 (6)
(6)
для любых t ≥ ta, ta = t0 + θa, t0 ≥ 0, где θa – время адаптации, или предельное соотношение
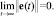 (7)
(7)
В работе [1] уравнения алгоритмов задают в общем виде:
z = A2(e, g, ξ, t), (9)
из них первое уравнение (7) соответствует параметрической настройке (ПН), а второе (8) – сигнальной настройке (СН). Структура системы показана на рис. 1.
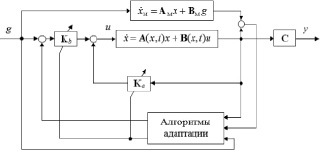
Рис. 1. Структурная схема системы с параметрической и сигнальной настройкой [4]
В работе [1] обосновывается рекомендация использовать для схемы на рис. 1 параметрическую настройку при существенном преобладании нестационарных свойств; сигнальную настройку при преобладании нелинейных свойств и совместно оба типа настройки при обоюдном проявлении нелинейных и нестационарных свойств.
Поскольку в рассматриваемой модели ГТУ в первую очередь проявляются нелинейные свойства, далее рассматривается САУ исключительно с сигнальной настройкой.
В качестве метода адаптации целесообразно выбрать метод функций Ляпунова из соображений сокращения времени поиска экстремума [1]. В работе [1] получен следующий алгоритм для сигнальной адаптации:
z(t) = –hsgn(BT Pe); h > 0, (10)
где (sgn BT Pe)i = sgn(BT Pe)i, матрица Р является решением матричного уравнения
PAT + ATP = –Q,
где матрицу Q рекомендуется выбирать диагональной (> 0).
Математическая модель
Поэлементная многорежимная динамическая математическая модель ГТУ содержит большое число нелинейных элементов и нелинейных связей и, как правило, требует последовательных приближений при проведении расчетов [2]. Поэтому для синтеза алгоритмов управления и испытания САУ ГТУ применяют упрощенные модели ГТУ, которые получают методом идентификации по данным натурного эксперимента или по данным, полученным на поэлементной многорежимной модели [5, 6].
Рассмотрим упрощенную динамическую модель ГТУ, полученную с помощью идентификации методом наименьших квадратов. Структура дифференциальных уравнений выбрана с учетом априорной информации об основных физических принципах преобразования энергии в ГТУ. Модель сохраняет допустимую адекватность для работы САУ ГТУ в режиме стабилизации частоты вращения свободной турбины ГТУ от холостого хода до 1,2 номинальной нагрузки. На рис. 2 изображена структурная схема полученной модели ГТУ.
На рис. 2 показана структура модели: nTS = f(GT) – нелинейная статическая характеристика, отражающая преобразование расхода топлива (кг/ч) в обороты турбокомпрессора (об/мин); T(nТК) – постоянная времени турбокомпрессора, зависящая от текущей частоты вращения турбокомпрессора; NE = f(nТК) – нелинейная статическая характеристика, отражающая преобразование частоты вращения турбокомпрессора (об/мин) в мощность свободной турбины (кВт); NG – мощность нагрузки (кВт); J (nСТ) – суммарный приведенный к валу свободной турбины момент инерции; nСТ – частота вращения свободной турбины (об/мин). Уравнения, описывающие динамические звенья на рис. 2, имеют следующий вид

Рис. 2. Структура нелинейной модели ГТУ
а) Уравнение ротора турбокомпрессора:
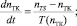 (11)
(11)
б) Уравнение свободной турбины:
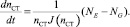 (12)
(12)
Эталонная модель получается из модели ГТУ (11), (12) линеаризацией вблизи точки номинального режима. Номинальный режим ГТУ – 2500 кВт. Эталонная модель включает в себя помимо уравнений собственно также регуляторы ГТУ. В режиме стабилизации nСТ основную роль играют два регулятора САУ ГТУ: регулятор частоты вращения свободной турбины nСТ и регулятор дозатора газа. Регуляторы включаются последовательно (рис. 3). Передаточная функция регулятора nСТ имеет следующий вид [8]:
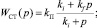 (13)
(13)
передаточная функция дозатора газа:
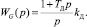 (14)
(14)
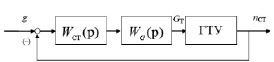
Рис. 3. Эталонная модель ГТУ
Регуляторы настроены на симметричный оптимум, что обеспечивает нулевую статическую ошибку по возмущению. Параметры линеаризованной эталонной модели ГТУ приняты следующими:
T(nТК) = 0,5 = const;
nTS/GT = const = k1 = 11,12;
NE/nТК = const = k2 = 0,26;
J(nСТ) = const = 2,88.
Тогда параметры регуляторов (13) и (14) для обеспечения (25) с Tμ = 0,1 будут следующими:
TД = 2; kД = 0,5; kf = 4;
ki = 10; kП = 5,67.
Сигнал задания
g = (nСТзад) = 5500 об/мин.
Вектор состояния представим в виде
x = (x1x2x3x4)T,
где x1 = nСТ, x2 = nТК, x3 – выход интегратора регулятора дозатора газа (14), x4 – выход интегратора регулятора nСТ (13). Тогда сигнальный алгоритм (10) получим в следующем виде:
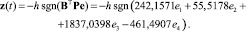 (15)
(15)
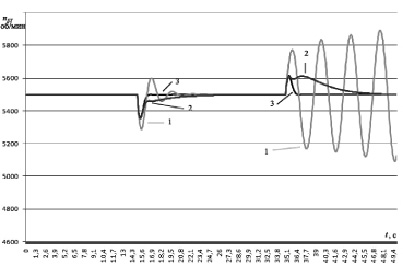
Рис. 4. Переходный процесс nСТ (частота вращения свободной турбины): 1 – нелинейная модель ГТУ с неадаптивной САУ; 2 – нелинейная модель ГТУ с адаптивной САУ; 3 – эталонная модель ГТУ
Для проведения эксперимента эталонная модель включается параллельно с нелинейной моделью ГТУ по схеме на рис. 1. В эксперименте учитывался только один вид нелинейности: зависимость T(nTK), при этом T меняется от 3 с (холостой ход 140 к Вт) до 0,5 с (номинальный режим 2500 кВт). На рис. 4 показано изменение во времени nСТ. В качестве возмущения задавалось изменение внешней нагрузки ГТУ f = (NG) по прямоугольному закону:
t = 0–15 с; NG = 140 кВт;
t = 15–35 с; NG = 2000 кВт;
t = 35–50 с; NG = 500 кВт.
На рисунке представлены три графика: эталонная модель ГТУ; нелинейная модель ГТУ с неадаптивной САУ (настройки регуляторов, как у эталонной модели); нелинейная модель ГТУ с адаптивной САУ (с эталонной моделью и сигнальной настройкой (15)).
Прочие переменные вектора x также успешно приближаются к переменным эталонной модели. Дальнейшие эксперименты показали достаточно высокую чувствительность рассмотренной системы с эталонной моделью к резким изменениям параметров нелинейной модели.
Исследования также показали, что если в уравнении алгоритма сигнальной адаптации (15) оставить только один сигнал
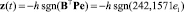
по внешней переменной – частоте вращения свободной турбины nСТ – то кратность изменения параметров может быть существенно повышена, качество регулирования по nСТ также значительно улучшается. Однако в этом случае по эталонной модели настраивается только nСТ, по остальным переменным x = (x1x2x3x4)T переходные процессы существенно отличаются от поведения эталонной модели, что, помимо прочего, ставит вопрос физической реализуемости. Поэтому целесообразно экспериментальным путем установить допустимую кратность изменения переменных (таблица).
В качестве критерия качества взят следующий критерий:
а) максимальное отклонение переменных САУ от эталонной модели не превосходит 15 %;
б) время переходного процесса не более чем в 5 раз превосходит время переходного процесса эталонной модели. В качестве условия устойчивости – нарушение устойчивости САУ.
В качестве модели 1 рассматривалась модель, представленная на рис. 2, при учете T(nТК) , но без учета нелинейных зависимостей:
NE = f(nТК), nTS = f(GT).
В качестве модели 2 – модель на рис. 2 с учетом всех нелинейностей:
T(nТК), NE = f(nТК), nTS = f(GT).
Допустимая кратность изменения переменных
|
Удовлетворяет критериям качества |
Удовлетворяет условию устойчивости |
|
|
Модель 1 с адаптивной САУ с одной переменной |
14 |
16 |
|
Модель 1 с адаптивной САУ с четырьмя переменными |
8 |
60 |
|
Модель 2 с адаптивной САУ с одной переменной |
8 |
16 |
|
Модель 2 с адаптивной САУ с четырьмя переменными |
2 |
5 |
Как видим из таблицы, диапазон кратности, удовлетворяющий условию устойчивости, значительно выше диапазона кратности, удовлетворяющего критериям качества, также выявлено, что диапазон измерений в линейной модели с адаптивной САУ шире, чем соответствующая ей нелинейная модель.
При введении ограничения по расходу топлива ситуация резко ухудшается.
Выводы
Методика адаптивного управления с эталонной моделью и сигнальной настройкой [1] в принципе может быть работоспособна при управлении ГТУ. Однако необходимо учитывать диапазон изменения параметров, что существенно влияет на результаты адаптации. Кроме того, следует учитывать физические ограничения, среди которых одним из ведущих является ограничение по расходу топлива GT. Полученные результаты требуют проведения на полученной основе дальнейших исследований.
Рецензенты:
Шулаков Н.В., д.т.н., профессор кафедры электротехники и электромеханики, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Казанцев В.П., д.т.н., профессор кафедры микропроцессорных средств автоматизации, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.




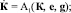 K = [Ka; Kb]; (8)
K = [Ka; Kb]; (8)