Пассивные системы виброзащиты (подрессоривания) с постоянными характеристиками транспортных средств являются наиболее распространенными в настоящее время. Потенциальные возможности подобных систем виброзащиты в удовлетворении требований к плавности хода транспортных средств ограничены. В связи с этим пассивные системы сдерживают повышение виброзащиты водителя, комфортности пассажиров, сохранности перевозимых грузов, виброзащиты собственных агрегатов и узлов транспортного средства и препятствуют росту эксплуатационных скоростей его движения. В связи с этим создание управляемых систем виброзащиты с целью повышения плавности хода транспортных средств является актуальной проблемой, одним из путей ее решения является построение электромеханических виброзащитных систем [4].
Целью данных исследований является рассмотрение возможностей повышения демпфирующих свойств системы пассивной виброзащиты за счет дополнения ее управляемым электромагнитным элементом.
В качестве амортизирующих конструкций в виброзащитных системах различных объектов могут быть использованы: пружинные, гидравлические, пневмогидравлические, пневматические, инерционные, резиновые, пластические амортизаторы. Опыт эксплуатации виброзащитных систем крупногабаритных объектов показал, что весьма перспективными являются пневматические упругие элементы на основе резинокордной оболочки (РКО).
В таких устройствах отсутствует металлический контакт между подрессоренными и неподрессоренными частями амортизируемого объекта (АО), и передача вибрационных нагрузок осуществляется через резинокордную стенку и сжатый рабочий газ [2]. Подобный амортизирующий элемент имеет множество достоинств, таких как высокая грузоподъемность, низкая цена, повышенная плавность хода автотранспортных систем на основе этого элемента. Для улучшения характеристик гашения колебаний в данный пневматический элемент предлагается внести управляемый электромагнитный компенсатор жесткости соленоидного типа, аналогично техническому решению по патенту № 2481506 [5]. В устройстве используется РКО Н-48.
Для исследования виброзащитной системы рассмотрены свободные колебания в одностепенной системе. Свободные колебания АО и давление рабочего газа пневмоамортизатора (ПА) с электромагнитным компенсатором описываются следующей математической моделью [1]:
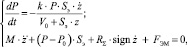(1)
где Р – текущее давление рабочего газа (воздуха) в резинокордной оболочке; P0 – давление в резинокордной оболочке ПА при статическом положении; z0 – высота подъема АО; V0 – рабочий объем ПА при статическом положении АО; M, g – масса амортизированного объекта и ускорение силы тяжести; k – показатель адиабаты; Sэ – эффективная площадь ПА; z, 
– относительные перемещения, скорость и ускорение АО; Rå – сила трения в РКО; Fэм – электромагнитная сила, развиваемая компенсатором.
В случае пассивной виброзащитной системы Fэм = 0 Н.
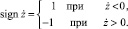(2)
При составлении уравнений приняты следующие допущения.
1. Рабочий газ в ПА подчиняется законам идеальных газов.
2. Температура окружающей среды постоянна и равна Тс.
3. Рабочий процесс в ПА считается адиабатическим.
4. Движение АО происходит только в вертикальном направлении.
5. Эффективная площадь (Sэ) ПА при движении АО не меняется.
6. Утечки газа из ПА отсутствуют.
7. R∑ = 0,01 Mg (для случая примененной резинокордной оболочки Н-48, определено экспериментально).
В процессе исследования была создана модель пневмоамортизатора в программном комплексе Matlab-Simulink (рис. 1). Начальные условия для системы: при t = 0, z = z0 = 0,1 м,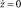 
. В модель введен импульсный электромагнитный генератор силы в качестве компенсатора жесткости, который создает расчетное противодействующее усилие упругой силе пневмоамортизатора.
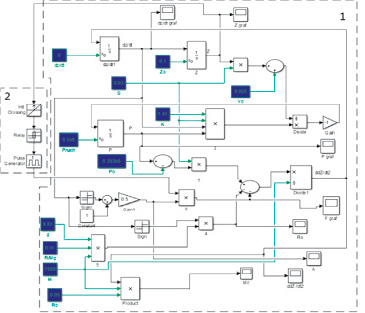
Рис. 1. Имитационная модель пневматического амортизатора (1) с устройством демпфирования колебаний (модель компенсатора жесткости в виде генератора линейного усилия) (2)
Модель позволит определить параметры технического задания для проектирования электромагнитного компенсатора жесткости пневматического упругого элемента виброзащитной системы, ориентированной на нагрузки порядка 1 тонны и выше. Данный тип компенсатора обладает следующими преимуществами: управляемость, изменяемые параметры усилия, адаптивные характеристики в зависимости от профиля дороги, высокая эксплуатационная надежность, необслуживаемость и др.
Было проведено исследование влияния значения электромагнитной силы компенсатора жесткости на время переходного процесса при гашении колебаний (рис. 2). Введение в состав виброзащитного устройства компенсатора жесткости позволило сократить время свободных колебаний с 12 до 8,4 с при использовании компенсатора только на ходе отбоя. В ходе исследования было установлено, что оптимальным является усилие в 400 Н, так как на дальнейшее уменьшение времени переходного процесса требует приложения больших сил и больших энергозатрат (рис. 2).
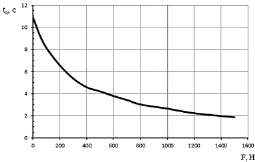
Рис. 2. Зависимость времени переходного процесса от амплитуды электромагнитной силы компенсатора жесткости
Исходя от габаритных размеров пневмобаллона и необходимого усилия, были рассчитаны параметры соленоида и его режима работы: сечение провода – 3 мм2, амплитуда тока при повторно-кратковременном режиме работы – 20 А, количество витков – 330, количество слоев – 10, внешний шихтованный магнитопровод из электротехнической стали 3411(Э310).
В ходе исследований в комплексе программ «ELCUT 5.6 Профессиональный» оценивалось влияние различных материалов сердечника на силу втягивания сердечника. Так, при полностью втянутом сердечнике сила, рассчитанная программным комплексом ELCUT, составляет 0,023 Н, что подтверждается теорией и может быть принято за погрешность. Параметры задачи в ELCUT: тип задачи – магнитостатика, модель осесимметричная, число ампер-витков обмотки – 6600, относительная магнитная проницаемость (μ/μ0) обмотки – 1, μ/μ0 электротехнической стали – 4000, модель окружена воздухом, граничные условия – магнитный потенциал, равный нулю. При расчетах принималось, что сердечник выдвинут из катушки на 10 мм.
В ходе расчетов было определено, что сила, развиваемая соленоидом при заданных габаритах и стальном сердечнике, имеет значение ~150 Н.
Математическая модель соленоида описывает процессы в электрической подсистеме на основе уравнения, составленного по второму закону Киргоффа:
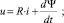
Ψ = L(x)∙i;
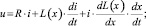
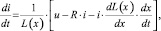(3)
где u – номинальное напряжение питания соленоида; R – сопротивление катушки соленоида; L(x) – индуктивность катушки соленоида; i – ток в катушке соленоида; x – координата перемещения сердечника соленоида; Ψ – потокосцепление катушки соленоида.
На основе магнитного сопротивления магнитной цепи соленоида определим его индуктивность в виде зависимости от координаты перемещения сердечника соленоида:
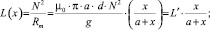
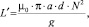(4)
где Rm – магнитное сопротивление системы; μ0 – магнитная проницаемость вакуума; N – число витков катушки соленоида; L – индуктивность соленоида; a – толщина магнитопровода; d – ширина воздушного зазора в магнитопроводе; g – величина воздушного зазора между сердечником и катушкой.
Электромагнитная сила определяется в предположении линейной магнитной системы и постоянства тока при изменении координаты перемещения сердечника соленоида:
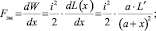
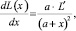(5)
где W – энергия магнитного поля соленоида.
Модель соленоида, реализованная в программном комплексе Matlab-Simulink, включена в модель виброзащитного устройства (рис. 4). В ходе исследований использовался неуправляемый импульсный источник питания соленоида с частотой, соответствующей частоте собственных колебаний виброзащитного устройства с амортизируемым объектом, – 1,25 Гц, период – 0,8 с, длительность импульса – 35 % периода, амплитуда импульсов питания – 12 В.
В ходе исследования имитационных моделей построены временные графики колебаний, тока в обмотке, напряжения и давления в пневматической подушке (рис. 3). Из анализа графиков видна разница между имитационными моделями, при переходе от идеального генератора линейного усилия к имитационной модели соленоида (рис. 4), время гашения колебаний увеличивается незначительно (на величину порядка 10 %).
Результаты моделирования работы электромагнитного компенсатора жесткости в составе пневматического виброзащитного устройства: максимальная сила, развиваемая соленоидом со стальным сердечником ~ 150 Н, максимальный ток в обмотке соленоида ~20 A, среднее значение тока ~ 7,57 A, исходя из среднего значения тока возможно уменьшение сечения провода катушки до 2 мм2, время затухания колебаний – 8,41 с.
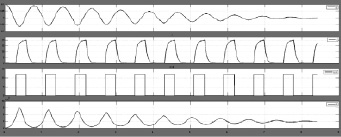
Рис. 3. Графики перемещения, тока в обмотке, напряжения питания и давления в пневматическом амортизаторе соответственно
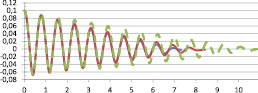
Рис. 4. Сравнение свободных колебаний (штрих-пунктирная линия), виброзащитного устройства с генератором линейного усилия (сплошная линия), модели соленоида (штриховая линия) при усилии в 150 Н
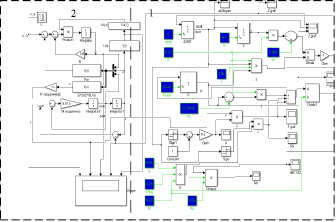
Рис. 5. Имитационная модель электропневматического устройства (1) с электромагнитным компенсатором жесткости (2)
В транспортных средствах, очевидно, необходимо сделать привязку управляющих сигналов соленоида к одному из регулируемых параметров виброзащитной системы, в качестве которых возможно выбирать, например, вертикальную координату колебаний амортизируемого объекта [3], давление рабочего тела в пневмобаллоне [1] и др.
Таким образом, введение в состав виброзащитного устройства компенсатора жесткости позволяет сократить время свободных колебаний до 25–40 % при использовании компенсатора только на ходе отбоя. Внедрение подобных систем требует дополнительных исследований возможностей различных конструкций компенсаторов, их оптимизации, алгоритмов их работы в различных дорожных условиях, возможностей системы энергообеспечения транспортного средства.
Рецензенты:
Харламов В.В., д.т.н., профессор, зав. кафедрой «Электрические машины и общая электротехника», Омский государственный университет путей сообщения, г. Омск;
Федоров В.К., д.т.н., профессор, кафедра технического сервиса, механики и электротехники, Омский государственный аграрный университет имени П.А. Столыпина, г. Омск.