Напряженное состояние металла определяется тремя параметрами: расстоянием r от начала координат до рассматриваемой точки, углом θ и параметрами KI, KII или KIII (рис. 1). Эти параметры носят название коэффициентов интенсивности напряжений. Они зависят от формы тела, внешних нагрузок, расположения и длины трещин.
Анализ прочности и долговечности детали с трещиной при циклическом нагружении в рамках линейной механики разрушения состоит из следующих этапов [7]:
● определение формы, размера и местоположения наиболее опасных исходных трещиноподобных дефектов;
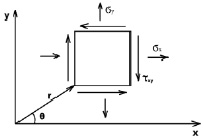
Рис. 1. Система координат и компоненты напряжений у кончика трещины
● определение напряженно-деформируемого состояния детали с детальным анализом поля напряжений вблизи трещин и определением коэффициентов интенсивности напряжений;
● выбор критерия локального разрушения на фронте трещины, изучение докритического развития трещины и отыскание критического (предельного) состояния, которое соответствует выходу конструкции на нерасчетный режим (например, разрушение).
Вычисленное значение наибольшего коэффициента интенсивности напряжений KI (как определенной функции нагрузок, размеров тела и длины начальной трещины) приравнивается некоторому критическому значению этого коэффициента, характеризующему сопротивление материала отрыву на фронте трещины нормального разрыва. Получается критериальная зависимость, связывающая допускаемые величины внешних нагрузок, длин трещин, внутренних напряжений, температурных градиентов и т.д. В случае устойчивого развития хрупких трещин эта зависимость служит для определения длины трещины.
Таким образом, одна из основных задач, стоящих перед механикой разрушения в связи с расчетом на прочность, состоит в определении коэффициента интенсивности напряжений, непосредственное влияние на который оказывает коррозионная среда.
Определим коэффициент интенсивности напряжений с учетом влияния водорода.
Рассмотрим развитие трещины последовательными скачками, величина которых значительно больше раскрытия трещины 2v0 в ее конце. Таким образом, для определения концентрации протонов водорода с приходим к следующей краевой задаче математической физики: в конце неподвижного полубесконечного прямолинейного разреза в твердом теле вдоль y = 0, x < 0 в начальный момент времени t = 0 включается постоянно действующий точечный источник протонов интенсивности Q. Предполагается, что величина Q не зависит от времени, а берега разреза свободны от нагрузок. Требуется найти распределение концентрации протонов в теле.
Уравнение, описывающее процесс диффузии протонов, имеет вид [7]
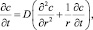(1)
при 0 < r < ∞, 0 < t < ∞ (r2 = x2 + y2), где D – коэффициент диффузии водорода в металле.
Уравнение сохранения массы [5]:
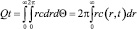(2)
играет роль дополнительного условия (при r → ∞ величина c стремится к нулю).
Решение этой задачи имеет следующий вид [5]:
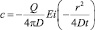. (3)
Здесь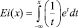 
– интегральная показательная функция. Напомним, что функция –Ei(–x) при положительных x монотонно убывает, причем имеют место следующие асимптотические формулы:
при x → 0 –Ei(–x) = –lnx – C (C ≈ 0,577 – постоянная Эйлера);
при x → ∞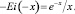 
Вследствие диффузии протонов вблизи конца трещины внутри пластической области образуется круговая область охрупченного металла, который ведет себя как упругое тело «упругое ядро» (рис. 2).
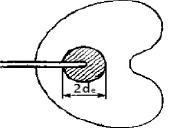
Рис. 2. «Упругое ядро»
Охрупчивающее действие протонов на металл определяется их концентрацией; поэтому будем считать для простоты, что, пока концентрация с меньше некоторой критической величины ce, металл остается в пластическом состоянии, а как только величина с превысит значение ce, металл переходит в упруго-хрупкое состояние.
При этом радиус охрупченного кругового ядра de находится по формуле (3) из условия:
при r = dec = ce.
Отсюда
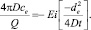(4)
Таким образом, величина de монотонно растет во времени.
Так как радиус упругого ядра гораздо больше раскрытия трещины, вблизи конца трещины формируется структура, характерная для математических разрезов в упругих телах.
Эта структура вполне характеризуется локальным коэффициентом интенсивности напряжений kI.
Найдем локальный коэффициент интенсивности KI. Он определяется из решения плоской задачи теории упругости для круговой области радиуса de с радиальным разрезом; на границе круга заданы нормальные и касательные нагрузки, зависящие только от параметра σs. Объемные силы в упругом ядре также зависят только от параметра σs.
Следовательно, коэффициент KI из соображений анализа размерностей равен
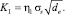(5)
Здесь η1 – некоторое постоянное число (в принятой постановке задачи оно не зависит обычно даже от коэффициента Пуассона или отношения σs/E и в принципе всегда может быть найдено, если известно решение соответствующей упруго-пластической задачи).
Интенсивность Q прямо пропорциональна величине раскрытия трещины в ее конце [7]:
Q = ηv0, (6)
так как свежая поверхность обнажающегося вследствие пластической деформации металла, очевидно, пропорциональна v0. Коэффициент η зависит от среды и от адсорбционной активности по отношению к водороду контакта свежий металл – среда.
Раскрытие v0 трещины равно
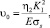(7)
(η2 – некоторое число).
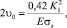(8)
η2 = 0,21.
Сравнивая с (6), получаем
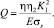(9)
Сравнивая с (3), в итоге получаем, что коррозионная среда имеет непосредственное влияние на коэффициент интенсивности напряжений:
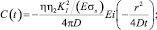(10)
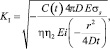(11)
где σs – предел текучести на растяжение, кг/мм2; E – модуль Юнга, Н/мм2; KI – КИН, Н/мм3/2; η2 = 0,21.
Коэффициент диффузии водорода в металлах D зависит от абсолютной температуры T, так [2]:
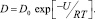(12)
Здесь U – энергия активации процесса; D0 – некоторая постоянная металла. Величины D0 и U для стали изменяются в пределах: D0 = 10–2–10–3 см2/с; U = 3–9 ккал/(г∙атом);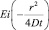 
– интегральная показательная функция; CH(t) – концентрация водорода, мг/кг.
Контакт с внешней средой и приложенное действие растягивающих механических напряжений вынуждает дислокационную структуру к перестройке, в результате чего происходит выход дислокаций на границу раздела металл/коррозионная среда и образование ступеньки скольжения с высотой, кратной вектору Бюргерса (рис. 3). При этом ступеньки скольжения образуют анодную и катодную поверхности. Анодный процесс инициирует водородную деполяризацию и абсорбцию водорода металлом [1].
А это приводит к дополнительным растягивающим напряжениям в кристаллической решетке конструкционного материала и водородной хрупкости.
Именно площадки ступенек скольжения определяют скорость растворения дислоцированных атомов и число перешедших на катод валентных электронов. В свою очередь, электроны соединяются с протонами и образуют адсорбированные атомы водорода:
H+ + e– = Hадс.
Чем больше площадь ступенек скольжения, тем выше скорость генерации атомарного водорода, адсорбирующегося на границе раздела металл/коррозионная среда на металле. Большая часть адсорбированного водорода объединяется в молекулы газа водорода, а меньшая – поглощается объемом металла (рис. 4) [1].
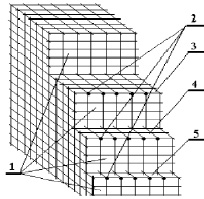
Рис. 3. Схема образования ступенек скольжения на границе раздела «металл/коррозионная среда»: 1 – границы раздела «металл/коррозионная среда»; 2 – дислоцированные атомы в ступеньке скольжения; 3, 4, 5 – ступеньки скольжения с высотами 4b, 2b и 1b
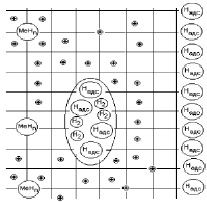
Рис. 4. Формы существования адсорбированного водорода Hадс – адсорбированный водород; H2 – молекулярный водород; Å – протон; MeHn – гидрид металла с валентностью n
Наводороживание сталей перлитного класса в деаэрированной воде описывается детерминистским уравнением кинетики данного процесса, полученным на кафедре АЭС МЭИ (ТУ) [1]:
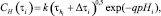(13)
где k и q – константы, определяемые при обработке данных целевых экспериментов; 
– вспомогательный параметр, имеет размерность экспозиции, необходимой для накопления такого же количества водорода, как за весь предшествующий период эксплуатации, но при значении pHi
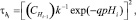(14)
где Δτi – интервал времени наблюдений между двумя последовательными измерениями, в пределах которого все значения фактор-аргументов неизменны.
В настоящее время нет методики описания процесса наводораживания аустенитных хромоникелевых сплавов (АХНС). В рамках данной статьи предлагается следующий алгоритм.
Накопление водорода в сталях аустенитного класса происходит в соответствии с законом Фарадея при извлечении хлорида хрома (CrCl3) из АХНС. Одному заряду хлор-иона (Cl–) при количестве электричества в 96500 Кл соответствует 1 г водорода (H+).
Зная, что аустенитные стали также подвержены водородному охрупчиванию, как и стали перлитного класса, выведем формулу для накопления водорода в стали 08Х18Н10Т.
Для этого преобразуем детерминированное уравнение кинетики наводораживания сталей перлитного класса при кипении воды (13) с учетом концентрирования хлорид-иона в воде при кипении в отложениях на теплообменной трубке.
Из формулы (13) выразим значение pH при наводораживании в кипящей воде:
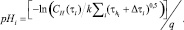(15)
В выражении, описывающем долговечность АХНС марки 08Х18Н10Т [5]:
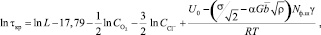(16)
где τкр – время до образования сквозной коррозионной трещины, ч; L – толщина стенки металла, мм;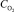 
– концентрация кислорода, мг/кг; 
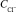– концентрация хлорид-иона, мг/кг; U0 – энергия активации процесса самодиффузии дислоцированного атома, кДж/моль; σ – суммарное растягивающее механическое напряжение, Н/м2; α – коэффициент, который зависит от механизма упрочнения и от сил сопротивления; G – модуль сдвига, Н/м2; 
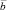– вектор Бюргерса, м; ρ – плотность дислокаций; Nф.ш – постоянная Авогадро по физической шкале, моль/г∙моль; γ – активационный объём, м3.
Учтем образование адсорбированного водорода, и, подставив в это выражение значение pH, получим время до образования сквозной коррозионной трещины.
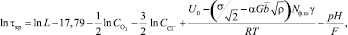(17)
где pH – водородный показатель (отрицательный десятичный логарифм концентрации ионов водорода); F – число Фарадея, Кл/моль∙экв.
И в конечном итоге, получаем формулу для накопления водорода для стали 08Х18Н10Т:
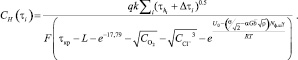(18)
Водород, несомненно, играет важную, но не исключительную роль при коррозионном разрушении под напряжением (КРПН) конструкционных материалов (сталей перлитного и аустенитного классов), т.к. в условиях активного растворения идет интенсивное наводораживание этих сталей. Однако эти процессы могут описывать только определенную часть КРПН.
Итак, основной причиной коррозионно-механических повреждений трубок теплообменной поверхности парогенераторов АЭС с ВВЭР-1000, изготовленных из аустенитной нержавеющей стали, является хлорид-кислородное коррозионное растрескивание [3]. Однако в результате химических отмывок ТОТ от отложений моющими композициями и непреднамеренного заброса ионообменных смол и промывочных растворов из БОУ (блочной обессоливающей установки) с питательной водой в ПГ, а также длительной его эксплуатации при низком числовом значении pH воды продувки происходит наводороживание аустенитной стали марки 08Х18Н10Т. Таким образом, водородная хрупкость также повреждает металл трубчатки ПГ, как и стали марки 10ГН2МФА, из которых изготовлены коллекторы ПГ.
В качестве основного критерия, который определяет повреждаемость элементов ПГ, выбрана трещиностойкость материала. Количественной характеристикой трещиностойкости материала является коэффициент интенсивности напряжений KI в вершине трещины. Предложена методика оценки остаточного ресурса трубных пучков и коллекторов для находящихся в эксплуатации парогенераторов с использованием зависимости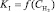 
.
Анализируя полученные результаты, можно отметить, что: коррозионно-активная среда вносит серьезный вклад в определение напряженно-деформируемого состояния конструкции; в зависимости от уровня водородного показателя интенсивность накопления водорода различна, соответственно, существенно различается и кинетика роста коэффициента интенсивности напряжений; проведение анализа прочности и долговечности конструкций, эксплуатирующихся в сложных условиях, без учета влияния коррозионной среды, но лишь с учетом введения поправочных коэффициентов, зачастую неоправданно. Таким образом, влияя на параметры коррозионной среды (в частности на водородный показатель), можно влиять на срок безаварийной службы оборудования АЭС, что вносит свой вклад в улучшение экономических показателей объекта.
Рецензенты:
Парфенов Ю.В., д.т.н., профессор, заведующий кафедрой АЭС НИУ МЭИ, ФГБОУ ВПО «Научно-исследовательский университет «Московский энергетический институт», г. Москва;
Горбатых В.П., д.т.н., профессор, преподаватель кафедры АЭС НИУ МЭИ, ФГБОУ ВПО «Научно-исследовательский университет «Московский энергетический институт», г. Москва.