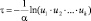Существенное значение для эффективного функционирования различных отраслей страны, в том числе и нефтеперерабатывающей, имеет выбор оптимальной стратегии ее развития в условиях рыночной экономики. Одним из важнейших факторов функционирования и развития данной отрасли является обеспечение оптимального соотношения между спросом и производством нефтепродуктов. Для решения указанных проблем применение классических экономико-математических моделей не приводит к желаемым результатам из-за высокой степени нестационарности и стохастичности основных параметров и показателей данной отрасли. В предлагаемой работе на базе известных подходов к построению имитационных моделей производства, заложенных в основополагающих трудах [1–3] и в исследованиях [9–10], учитывающих отраслевую специфику, а также в предыдущих публикациях авторов данной статьи [6–8], предлагается обобщенная имитационная модель нефтеперерабатывающей отрасли для анализа влияния нестационарности и случайности спроса и предложения на эффективность функционирования отрасли.
Функциональная структура системы производства и реализации нефтепродуктов
Функциональная структура системы представлена на рис. 1 и наглядно отражает как производственные, так и информационно-управляющие функции.
Моделирование спроса на нефтепродукты может быть осуществлено двумя путями: аналитическим и статистическим. Первый путь предполагает получение эконометрических зависимостей спроса от различных факторов, где существенную роль играют спрос в предыдущий период и индексы розничных цен. Блоки 2–5 связаны с уровнем основных производственных фондов отрасли, которые косвенно определяют функции оставшихся четырёх блоков (6–9). Также следует отметить наличие значительной корреляции между функциями всех звеньев приведенной структуры.
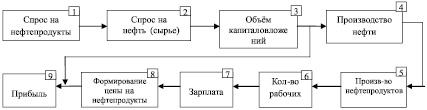
Рис. 1. Функциональная структура системы
Перед тем как разрабатывать модель системы, рассмотрим обобщенные показатели функционирования отрасли. Как следует из функциональной структуры, рассматриваемая система состоит из двух подразделений: производство нефти и производство нефтепродуктов. Первое подразделение поставляет сырье для второго. Приведем аналитические зависимости для описания обобщенных показателей этих подразделений. Пусть Φ1(t) – основные производственные фонды в стоимостном выражении первого подразделения, а Φ2(t) – основные производственные фонды второго подразделения, x1 – стоимость конечного продукта (нефти) первого подразделения, а x2 – стоимость конечного продукта (нефтепродукты) второго подразделения. N1 и N2 – потоки капиталовложений в эти подразделения. Напишем выражения для производственных функций этих подразделений:
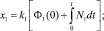
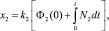
где k1 и k2 – коэффициенты фондоотдачи.
Управляющим параметром является l – доля от общей суммы накопления, направляемой в первое подразделение. Примем, что
N1 = λx1; N2 = (1 –l)x2; 0 ≤ l ≤ 1.
Полученным зависимостям можно поставить в соответствие следующую кибернетическую схему (рис. 2) [1].
Используя выражения передаточных функций для последовательного соединения и обратной связи, получим операторную форму для x1 и x2.
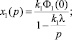
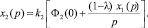
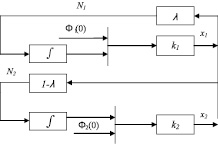
Рис. 2. Кибернетическая схема системы
Преобразуя эти выражения, получим
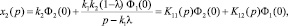
где K11(p) = k2 и 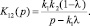
Тогда переход от операторной формы к оригиналу приводит к выражению
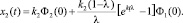
Из этого выражения видно, что стоимость производственных фондов в начальный момент (t = 0) приводит к увеличению выпуска нефтепродуктов для всех t > 0. Также очевидна важная роль параметра l, т.е. чем большая часть накопления направляется в производство нефти, тем выше интенсивность развития отрасли. Однако множитель (1 – l) при показательной функции не позволяет l принимать слишком большие значения, так как при l = 1 второе слагаемое уравнения может оказаться равным нулю. Поэтому важным является выбор значения параметра l, который можно аналитически оптимизировать по различным критериям принятия решений, или для нахождения эффективного значения l можно использовать методы имитационного моделирования. Обобщенные показатели, полученные в этом разделе, должны послужить ориентиром при анализе результатов имитационного моделирования по другим, например эконометрическим, моделям.
Построение модели функционирования системы
Пусть к началу некоторого периода отрасль располагает основными производственными фондами в стоимостном выражении Ф(t). На основе технических и технологических показателей определяется коэффициент максимальной фондоотдачи km. Тогда для потенциально возможной производственной мощности отрасли имеем выражение
M(t) = kmФ(t), (1)
где Ф(t) = Φ1(t) + Φ2(t); Φ1(t) = l∙Ф(t);
Φ2(t) = (1 – l)∙Ф(t).
А для достижимой или фактической производственной мощности отрасли имеем соответственно, соотношение
G(t) = kфФ(t), (2)
где kф ‒ коэффициент фактической фондоотдачи.
Указанные показатели являются базовыми для производственной характеристики отрасли к началу рассматриваемого периода. Руководство отрасли на основе маркетинговых исследований спроса формирует плановое задание по выпуску продукции. Пусть R(t) – выражение величины спроса, определяющее плановое задание по выпуску продукции. Осуществим предварительную оценку напряженности планового задания.
Вариант 1
Если
R(t) > M(t), (3)
то плановое задание может быть выполнено только при условии введения новых мощностей.
Вариант 2
Если
G(t) < < M(t), (4)
то план может быть выполнен только при реализации инноваций, повышающих коэффициент фактической фондоотдачи.
Вариант 3
Если
R(t) ≤ G(t), (5)
то необходимо проведение мероприятий, направленных на увеличение спроса путем совершенствования качества и ассортимента продукции.
Для описания и анализа динамики функционирования системы целесообразно [3, 11] построить эконометрическую модель в виде рекуррентных соотношений.
Очевидно, отправным значением для определения спроса на нефтепродукты в текущее время R(t) является спрос в предыдущий период R(t – 1). Разтличие между ними обусловлено рядом факторов, из которых наиболее существенным является отношение между месячным доходом населения MD и индексом розничных цен на товары потребления IS, а также затратами на рекламу А. Влияние на величину спроса других неучтенных факторов можно учесть с помощью случайной величины W1 c заданным законом распределения. Тогда с помощью аппарата множественной линейной регрессии построим соотношение
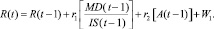 (6)
(6)
Блок «Производство нефтепродуктов» определяется рекуррентным соотношением
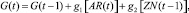 (7)
(7)
где G – индекс производства нефтепродуктов; АR – усредненный объем реализации нефтепродуктов за предыдущий интервал времени (например, три месяца); ZN – запасы нефтепродуктов в точках реализации в предыдущем периоде.
Блок «Спрос на нефть (сырье)» описывается уравнением
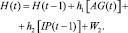 (8)
(8)
Здесь Н – величина спроса; AG – усредненный индекс производства нефтепродуктов за предыдущие шесть месяцев; IP – индекс производства товаров длительного пользования; W2 – случайная величина c заданным законом распределения, учитывающая влияние на величину спроса других неучтенных факторов.
Уравнение для определения капиталовложений К имеет вид
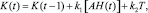 (9)
(9)
где АH – среднемесячный объем реализации нефти за предыдущий интервал времени (например, полугодие); T ‒ тренд.
Индекс производства нефти Q зависит от спроса на нее, отношения запасов в нефтехранилищах к объему текущих заказов на ее поставку INV/UO в предыдущий период, времени года М, тренда Т и определяется выражением
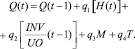 (10)
(10)
Количество рабочих N, занятых в отрасли, определяется ее производством в данном и в трех предыдущих месяцах [AQ(t – i)], а также отношением между месячным доходом населения MD и индексом розничных цен на товары потребления IS, характеризующим реальные доходы населения в предыдущий период
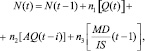 (11)
(11)
Для определения заработной платы E, кроме числа рабочих, необходимо учесть и значение тренда
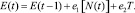 (12)
(12)
Текущий индекс цен Р на нефтепродукты определяется отношением его запасов к заказам INV/UO в предыдущем периоде, средней зарплатой Е по отрасли, предыдущими значениями индексов цен на сырье B и трендом Т
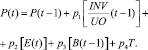 (13)
(13)
Уравнения модели отрасли завершает выражение для вычисления прибыли D
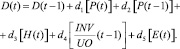 (14)
(14)
Здесь кроме индекса цен на нефтепродукты (Р) учитываются цена и объем продаж нефти. Непосредственно учтенным фактором затрат является заработная плата и затраты, связанные с сырьем, которые косвенно отражены стоимостью запасов и фигурируют в отношении запасов к заказам.
Все коэффициенты (r, g, h, k, q, n, e, p, d) в моделях (6–14) определяются стандартным аппаратом регрессионного анализа.
Моделирование случайных параметров спроса
Значения параметров W1 и W2 являются непрерывными или целочисленными случайными величинами с заданными законами распределения, например в виде плотности распределенияφ(w). Для моделирования значений этих параметров можно применить метод обратной функции моделирования случайных величин, основанной на теореме 1 [5]: «Случайная величина W, реализации которой определяются из выражения
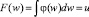 или w = F–1(u), (15)
или w = F–1(u), (15)
где u – случайное число, равномерно распределенное в интервале [0, 1], имеет плотность распределения φ(w)» или основным методом моделирования целочисленных величин, основанным на теореме 2: «Величина wk, заданная в виде таблицы 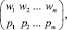 наступает с вероятностью pk при выполнении условия u ∈ ∆k, где ∆k = pk».
наступает с вероятностью pk при выполнении условия u ∈ ∆k, где ∆k = pk».
В случае невозможности реализации преобразования (15) или при задании законов распределения параметров W1 и W2 в графическом виде или в табличной форме можно воспользоваться методом исключения Джона фон Неймана, принцип работы которого непосредственно вытекает из теоремы 3 «Пусть u1 и u2 – случайные числа, равномерно распределенные в интервале [0, 1] и w = a + u1(b – a), y = Mu2, w ∈ [a, b], тогда случайная величина h, определенная из условия W = w при y < φ(w), имеет плотность распределения φ(w)». Доказательства данных теорем можно найти, например, в [5].
Если функция плотности j(w) относится к одному из известных стандартных теоретических законов распределения, то для моделирования значений w можно воспользоваться формулами, приведенными в таблице [4].
Формулы моделирования основных теоретических распределений случайных величин
|
Распределение |
Функции плотности |
Формула для моделирования |
|
Нормальное |
|
|
|
Равномерное |
|
τ = a + u(b – a) |
|
Экспоненциальное |
|
|
|
Линейное |
|
|
|
Гамма |
|
|
Наиболее полный перечень стандартных теоретических распределений непрерывных случайных величин и формул их моделирования приведен в [5].
Алгоритм моделирования процесса функционирования производства и реализации нефтепродуктов
Алгоритм моделирования процесса функционирования производства и реализации нефтепродуктов включает следующие шаги:
Шаг 1. Определение для заданного значения l потенциально возможной производственной мощности отрасли по (1).
Шаг 2. Определение фактической производственной мощности отрасли по (2).
Шаг 3. Определение значения спроса на нефтепродукты в текущее время по (6).
Шаг 4. Вычисление величины спроса на нефть (сырье) по (8).
Шаг 5. Вычисление значения капиталовложений по (9).
Шаг 6. Вычисление индекса производства нефти по (10).
Шаг 7. Вычисление значения индекса производства нефтепродуктов по (7).
Шаг 8. Вычисление количества рабочих, занятых в отрасли, по (11).
Шаг 9. Вычисление заработной платы по (12).
Шаг 10. Вычисление текущего индекса цен по (13).
Шаг 11. Вычисление значения прибыли по (14).
Шаг 12. Анализ соответствия полученных по формулам (2) и (7) значений производственной мощности.
Шаг 13. Анализ результатов предварительной оценки напряженности планового задания по вариантам (3–5).
Шаг 14. Определение эффективного значения параметра l, характеризующего распределение общей суммы капиталовложений между добычей нефти и производством нефтепродуктов.
Исследование планово-производственной деятельности предприятия различных отраслей на протяжении значительного периода времени дает возможность создать динамическую картину функционирования, в которой существенную роль играют такие факторы, как скорость роста стоимости основных производственных фондов, темп улучшения использования основных и оборотных фондов и скорость роста производительности труда.
Заключение
Сконструирована имитационная модель для анализа системы нефтеперерабатывающей отрасли, позволяющая на основе предложенного алгоритма функционирования производства и реализации нефтепродуктов выявить различные варианты ее развития в зависимости от коэффициентов фондоотдачи, неопределенного спроса и других показателей. Таким образом, построенная модель, предложенная в исследовании, позволяет выявить вариант оптимального соотношения между спросом и производством нефтепродуктов, а также способствует планированию выпуска продукции более эффективно.
Также применение результатов моделирования поможет выделить те приоритетные показатели системы нефтеперерабатывающих организаций, которые следует развивать с учетом имеющихся ресурсов.
Рецензенты:
Джурунтаев Д.З., д.т.н., профессор кафедры «Информационная безопасность», Казахский национальный технический университет имени К.И. Сатпаева, г. Алматы;
Айтчанов Б.Х., д.т.н., профессор кафедры «Информационные технологии», Казахский национальный технический университет имени К.И. Сатпаева, г. Алматы.




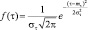 , –∞ < τ ∞
, –∞ < τ ∞
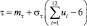
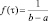 , τ ∈ [a, b]
, τ ∈ [a, b]
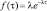 , τ ≥ 0
, τ ≥ 0
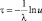
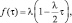
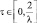
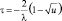
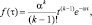 α > 0, k > 0, τ ≥ 0
α > 0, k > 0, τ ≥ 0