Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Структура технической системы в процессе её эксплуатации меняет свое содержание, что свидетельствует об изменении информации, количество которой можно определить через её меру. Сложность самой структуры, обусловленная количеством её элементов и топологией, накладывает свой отпечаток на определение искомых показателей. Если обратиться к вопросам обеспечения надежности функционирования системы, используя при этом параметры её структуры, то может быть затронута такая проблема, как наличие неопределенности информации. Решая её через количественную меру, можно решать задачи выбора наиболее информативной структуры из рассматриваемых альтернатив. Задачу выбора или «запомненного выбора» нельзя считать простейшей, поскольку речь здесь идет о применимости вероятностно-статистической методологии учета факторов неопределенности при наблюдении поведения системы. Согласно [6] применение в системах управления данной методологии в научных кругах остается спорным. Дело в том, что теория информации, помимо вопросов передачи информации, затрагивает решение задач определения её меры с учетом вероятностно-статистической методологии. Здесь факторы рассматриваются как случайные, порождающие неопределенность и учитываются через вероятностные показатели. Несмотря на критические замечания в [6], в процессе анализа надежности систем приходится опираться на статистические характеристики и на их основе усреднять результаты. Такие усреднения «сглаживают» статистические выбросы, то есть трудно предсказуемые события (например, аварии, приводящие к большому экономическому ущербу). Их также нельзя отнести к шумам статистического ряда. Тем самым получаемые оценки оказываются малоэффективными и смещенными, что приводит к потере точности расчетов. Поскольку погрешность порождена на начальном этапе (при определении статистической меры информации), то нельзя исключать факта её переноса на конечный результат после завершения эквивалентных преобразований. Однако иных, детерминированных решений в определении её количества пока не найдено.

Рассматривая состояние технической системы на основе меры неопределенности информации, приходится, опираясь на теорию вероятностей, строить (например, согласно [2, 3]) статистический ансамбль. В работе [3] рассмотрены статистические характеристики, связанные с распределением собственной (частной) информации как статистической функции дискретной случайной величины. Данная функция распределения собственной информации не исключает важности учета статистик в задачах оценки состояний системы. То есть, если исходить из свойств собственной информации, то можно с некоторой долей скептицизма использовать её для определения количества информации при эквивалентировании структур.

Особенности характеристик энтропии

Собственная информация I = log₂N о наличии N всевозможных состояний элементов определена Хартли и наделена свойствами неотрицательности, монотонности и аддитивности. Дискретная случайная величина I может быть задана рядом распределения, представляющего собой совокупность всех возможных отрицательных значений частных информаций I_i и соответствующих им вероятностей p_i [3]. Если обратиться к классической теории информации, в основе которой лежат работы К. Шеннона, то в ней информация определяется как мера или количество неопределённости (информационной энтропии). Статистический ряд распределения позволяет определить энтропийную (статистическую) меру количества информации по Шеннону:

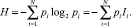(1)

Выражение (1) выполнимо при условии

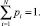
Вероятность, стоящая в (1) перед логарифмом, имеет свою специфическую особенность. Именно она связывает информацию с энтропией. В большинстве методов определения количества энтропии данная вероятность служит для усреднения количества энтропии. Например, при передаче информации по сети усреднение не накладывает свой отпечаток на искомый результат. Однако с позиции структурной надежности, когда, с одной стороны, статистические характеристики не устойчивы, а с другой – события приходится рассматривать как совместные, усреднение уведет оценки в область высокой погрешности. Поэтому вопрос о том, какую величину вероятности поставить перед логарифмом энтропии Шеннона, остается открытым. Одним из решений данного вопроса можно считать применение субъективной вероятности, связь которой с энтропией обозначена в работе [4]. Применение субъективной вероятности не лежит в русле настоящей работы, поэтому далее положим в основу классическое выражение (1), ограничившись предположением об усреднении энтропии.

В процессе эквивалентирования необходимо иметь структуру объекта, параметры его элементов и технологию преобразования структуры к единому элементу с параметрами, эквивалентными всей структуре. Исходные параметры структур (например, для таких систем, как трубопроводные, электроснабжения, компьютерные и др.), к которым отнесем вероятности состояний элементов, часто оцениваются посредством применения теорий вероятности и надежности.

Статистические характеристики структурной надежности имеют некоторую особенность в том, что каждому элементу системы присущи два противоположных дискретных состояния: работоспособное, с вероятностью p, и неработоспособное, с вероятностью q.

Рассматривая статистику потока противоположных состояний по каждому из элементов i, имеем совокупность 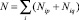состояний объекта. Эти раздельные состояния (при условии равновероятности событий) позволяют определить количество информации через собственные значения:

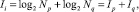(2)

где I_p и I_q – собственные значения информации и количество состояний N_p и N_q, относящихся к работе и отказу элемента i с вероятностями p и q соответственно.

Наличие противоположных состояний и предположение об их независимости, в оценках надежности систем требуют учета ещё одного свойства, присущего информации: противоположные события разделяют информацию по качественному признаку. В оценках структурной надежности, качественный признак – «работа – отказ», поэтому информация в (2) разделена на качественные составляющие. Следовательно, процесс эквивалентирования информации должен идти отдельно по каждому из противоположных состояний, поскольку при их слиянии утрачивается смысл оценки уровня надежности через меру информации [1]. Выражение (2) малопригодно для эквивалентирования, так как на практике вероятность работоспособного состояния всегда будет выше противоположной вероятности. Поэтому следует использовать формулы Шеннона (1).

Далее предложим к рассмотрению модель определения посредством эквивалентирования информационной энтропии с учетом качественного признака.

Определение энтропийных характеристик простейшей структуры

Структуру, состоящую из двух элементов, соединенных последовательно либо параллельно, будем считать простейшей. При этом не следует забывать, что при сопоставлении последовательных и параллельных структур между собой количество вероятных состояний резко отличается. Если число соединенных элементов структуры увеличить, то возрастет и количество состояний, что сделает работу по определению энтропии практически невозможной.

При построении математических функций эквивалентирования выделим ряд общих свойств:

1) энтропия исходного и энтропия эквивалентного состояния элементов выражается через вероятностные характеристики системы, полученные на основе статистики;

2) энтропийная характеристика последовательных и параллельных структур зависит от числа элементов и размерности пространства состояний;

3) энтропийная характеристика разделяет вероятностные состояния на два противоположных.

В основу построения энтропийных характеристик положим результаты исследований, представленные в работах [1, 5], а также в [2, 3], когда величина энтропии наложения и пересечения двух взаимосвязанных событий определяется через геометрическую площадь, образованную, с одной стороны, вероятностью события, с другой – собственной информацией, присущей событию.

Каждому элементу i структуры из статистического ряда присущи вероятности p_i + q_i = 1. Предположение о противоположности и независимости событий, присущих элементу, позволяет вычислить энтропию согласно выражению (1). Два элемента одновременно могут находиться в совместном состоянии, а их энтропийные характеристики H(p) для двух независимых событий, например, с вероятностями p₁ и p₂ имеют вид:

– для совместной энтропии (с учетом совместной вероятности p₁p₂)

H(p₁p₂) = – p₁p₂ log₂ p₁ – p₁p₂ log₂ p₂ = p₂H(p₁) + p₁H(p₂), (3)

где H(p₁) = – p₁log₂ p₁, H(p₂) = – p₂ log₂ p₂;

– для условной энтропии (с учетом условных вероятностей p₁/p₂ и p₂/p₁)

H(p₁/p₂) = H(p₁) – p₁H(p₂); (4)

H(p₂/p₁) = H(p₂) – p₂H(p₁); (5)

H(p₁/p₂) + H(p₂/p₁) = H(p₁) + H(p₂) – H(p₁∙p₂) = p₁ log₂ p₁ + p₂ log₂ p₂ – p₂H(p₁) – p₁ H(p₂). (6)

Выражения (3)–(6) не предусматривают разделение энтропии по качественному признаку. С тем, чтобы выполнить условие разделения, вновь обратимся к расчетам надежности системы, для которых применяют метод перебора независимых состояний элементов системы. Их полный перебор для двух элементов (n = 2) позволяет записать выражение, состоящее из 2ⁿ пересекающихся событий:

p₁p₂ + p₁q₂ + p₂q₁ + q₁q₂ = 1. (7)

Принимая во внимание определение совместной энтропии для вероятности p₁p₂ по выражению (3) и распространяя его аналогичным образом на три остальные совместные вероятности в (7), можно построить функцию определения суммарной энтропии двух независимых элементов:

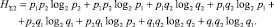(8)

Выражение (8) перепишем в виде

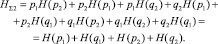(9)

Из (9) можно выделить энтропии:

– совместную,

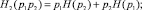(10)

– условную,

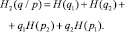(11)

В (10) свойство о разделении информации по качественному признаку имеет место, тогда как в (11) – не соблюдается. Чтобы распространить данное свойство на все составляющие энтропии, предлагается ввести нормировку её значений. Для элемента i структуры его нормированная энтропия определяется из выражения

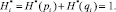(12)

Далее надстрочный символ (*) будет означать наличие в формулах нормированной величины энтропии. Кроме условия (12) представим дополнительное условие нормировки – суммарная нормированная энтропия равна числу элементов в структуре:

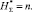(13)

Применив нормировку при условиях (12) и p_i + q_i = 1, выражение (9) с учетом преобразований будет иметь вид

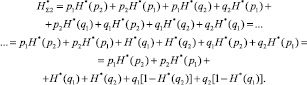(14)

Из (14) с учетом качественного признака выделим энтропии:

– совместную,

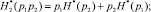(15)

– условную,

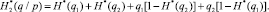(16)

Выражение для определения условной энтропии можно получить иным путем:

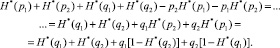(17)

Тем самым из (14) выделены качественные составляющие энтропии, которые будут применены для эквивалентирования.

Далее перейдем к рассмотрению трех элементов, которые одновременно могут находиться в совместном состоянии. Полный перебор для трех элементов (n = 3) позволяет записать выражение, состоящее из 2ⁿ пересекающихся событий:

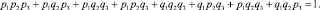(18)

По аналогии с (9) строится функция определения суммарной нормированной энтропии трех независимых элементов:

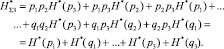(19)

Выражение (19) (в сокращенном виде), с учетом нормировки (12), (13) и p_i + q_i = 1, после преобразований перепишем в виде

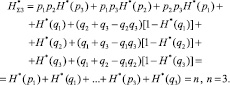(20)

Формула (20) включает в себя совместную и условную энтропии, разделенные по качественному признаку:

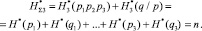(21)

Из выражения следует выделить:

– совместную энтропию,

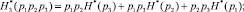(22)

– условную энтропию,

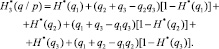(23)

Если в выражение (23) подставить q₃ = 0 и 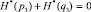, то можно перейти к условной энтропии для двух элементов, то есть к формуле (16).

Эквивалентные преобразования

Полученные выражения для определения совместных и условных значений энтропии, по сути, отражают её эквивалент. Далее покажем, какими будут математические выражения эквивалентных преобразований при переходе от двух к трем событиям, минуя выражения (22) и (23). Такие выражения будут полезны, например, при эквивалентировании последовательно-параллельных структур.

Для получения эквивалента совместной энтропии необходимы: вероятность p_э = p₁p₂ и энтропия 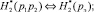энтропия H*(p₃) и вероятность p₃ третьего элемента. Эквивалент совместной энтропии, имея сходство с (15), определяется по выражению

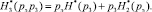(24)

Эквивалент условной энтропии можно определить через выражение

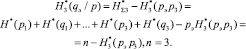(25)

Если в (25) раскрыть эквивалент совместной энтропии и выполнить ряд преобразований, можно перейти к выражению (23).

Поскольку выражения для эквивалентирования включают в себя нормированные значения энтропии, то при завершении расчетов следует перейти к определению искомых значений в битах.

Заключение

В процессе разработки проектов и эксплуатации технической системы, когда её структура подлежит простым эквивалентным преобразованиям, востребованы выражения для определения меры неопределенности информации. Для расчета количества информации применение формулы Шеннона в чистом виде весьма затруднительно. Поэтому расширив свойства информации и введя условие нормировки, построены математические выражения для эквивалентных преобразований.

Полученные выражения (24)–(25) позволяют найти эквивалент количества совместной и условной энтропии при последовательном или параллельном эквивалентировании элементов простейшей структуры технической системы.

Работа выполнена при поддержке гранта РФФИ №15-08-01473.

Рецензенты:

Гафнер Ю.Я., д.ф.-м.н., зав. кафедрой общей и экспериментальной физики, ХГУ им. Н.Ф. Катанова, г. Абакан;

Кочетков В.П., д.т.н., профессор кафедры электроэнергетики, Хакасский технический институт, филиал, Сибирский федеральный университет, г. Абакан.