Изучение природы температурных процессов в нефтяном пласте и построение аналитических зависимостей между доступными для прямых измерений величинами позволяет определить расчетными способами важнейшие физические параметры залежи и определить оптимальные режимы теплового воздействия. Аналитические решения задач обладают особой ценностью [8, 9], поскольку позволяют исследовать взаимосвязь полей и определяющих физических параметров в максимально широком диапазоне их изменения. Получение простых аналитических зависимостей представляет ценность как для инженерных расчетов [4], так и для качественной проверки (тестирования) более сложных моделей, особенно основанных на использовании конечно-разностных методов.
Применение квазистационарных моделей позволяет существенно расширить круг задач, обладающих аналитическими решениями, и поэтому они широко используется в теплофизике [16, 7], гидродинамике [3, 6], электродинамике [1] и других разделах науки.
В данной статье для исследования квазистационарного температурного поля в тонком слое, окруженном анизотропной средой, использован развитый авторами асимптотический метод решения задач сопряжения [10, 11].
Рассмотрим распределение температурного поля в пласте (θ, θ1 – температурное поле флюида и окружающей среды соответственно), представленном тремя областями с плоскими границами раздела zd = ±h. Центральный слой с теплопроводностью 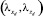 толщиной 2h является хорошо проницаемым и в горизонтальном и в вертикальном направлениях. Полагаем, что окружающие породы являются сильно анизотропными, и в них преобладает вертикальная теплопроводность
толщиной 2h является хорошо проницаемым и в горизонтальном и в вертикальном направлениях. Полагаем, что окружающие породы являются сильно анизотропными, и в них преобладает вертикальная теплопроводность 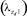 в сравнении с горизонтальной
в сравнении с горизонтальной 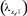 настолько, что можно пренебречь членами со второй производной по горизонтальным координатам в уравнениях для окружающей среды [17, 12]. Предположим также, что свойства покрывающих и подстилающих пород идентичны. На границе xd = 0 находится источник тепла с заданной температурой θ01 – Γzd, где θ01 – естественная невозмущенная температура Земли на границе zd = 0, Γ – геотермический градиент флюида.
настолько, что можно пренебречь членами со второй производной по горизонтальным координатам в уравнениях для окружающей среды [17, 12]. Предположим также, что свойства покрывающих и подстилающих пород идентичны. На границе xd = 0 находится источник тепла с заданной температурой θ01 – Γzd, где θ01 – естественная невозмущенная температура Земли на границе zd = 0, Γ – геотермический градиент флюида.
На рисунке представлена геометрия задачи в прямоугольной системе координат, ось zd которой перпендикулярна к границам раздела сред. Задача обладает трансляционной симметрией в горизонтальном направлении (по оси yd). Средний слой считается тонким, и в его пределах установление температуры происходит за короткий промежуток времени, вследствие чего частной производной по времени по сравнению со вторыми производными по пространственным переменным можно пренебречь 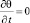 . Однако время входит в полученное таким образом стационарное уравнение в виде параметра (квазистационарное приближение).
. Однако время входит в полученное таким образом стационарное уравнение в виде параметра (квазистационарное приближение).
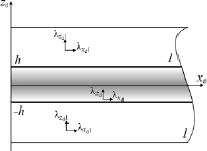
Геометрия задачи
Запишем постановку задачи в размерном виде [2]
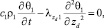
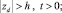 (1)
(1)
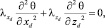
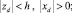 (2)
(2)
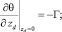 (3)
(3)
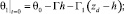
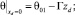 (4)
(4)
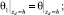
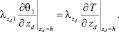 (5)
(5)
С использованием соотношений
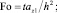
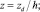
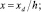
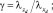
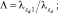
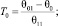
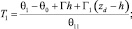
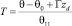 (6)
(6)
задача (1)–(5) приведена к безразмерному виду. В дальнейшем для простоты положим все коэффициенты в уравнениях равными единице (γ = 1, Λ = 1). Для использования асимптотических методов в задаче добавлен параметр асимптотического разложения путем умножения на 1/e первой и второй производных по z как в уравнениях, так и в граничных условиях.
Математическая постановка параметризованной температурной задачи в таких предположениях имеет вид
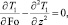
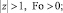 (7)
(7)
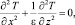
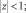
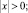 (8)
(8)
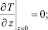 (9)
(9)
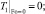
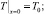 (10)
(10)
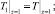
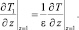 (11)
(11)
Предполагается, что решение является регулярным на бесконечности, т.е. при устремлении пространственных координат в бесконечность искомое решение, а при необходимости и его производная, обращается в нуль. Отметим, что решение исходной задачи может быть получено из решения параметризованной задачи при ε = 1.
Решение представляется функцией температуры T каждой из областей в виде асимптотической формулы по параметру ε [15, 18]
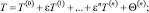
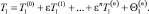 (12)
(12)
Подставив выражения (12) в (7)–(11) и сгруппировав слагаемые по степеням параметра разложения ε, получим
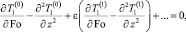
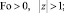 (13)
(13)
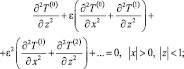 (14)
(14)
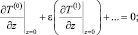 (15)
(15)
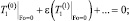
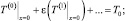 (16)
(16)
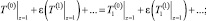
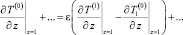 (17)
(17)
Уравнение (14) содержит соседние коэффициенты разложения, т.е. является «зацепленным». «Расцепление» уравнения (14) осуществлено с использованием разработанной ранее процедуры [13, 14, 19]. Устремив ε к нулю в уравнении (14), получим 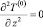 . Результат интегрирования, с учетом граничных условий (17), позволяет установить, что в нулевом приближении температура является функцией только от х и параметра Fo T(0) = T(0)(x, Fo). Следовательно, в нулевом приближении температура одинакова в каждой точке любого сечения, параллельного оси z.
. Результат интегрирования, с учетом граничных условий (17), позволяет установить, что в нулевом приближении температура является функцией только от х и параметра Fo T(0) = T(0)(x, Fo). Следовательно, в нулевом приближении температура одинакова в каждой точке любого сечения, параллельного оси z.
Поскольку 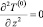 , то, поделив (14) на e и устремив его к нулю, получим
, то, поделив (14) на e и устремив его к нулю, получим
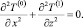 (18)
(18)
Так как T(0)(x, Fo) не зависит от переменной z, вспомогательная функция E(x, Fo), составленная из слагаемых уравнения (18), содержащих T(0), также не зависит от z. Тогда (18) можно представить как
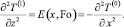 (19)
(19)
Проинтегрировав (19) по переменной z, найдем выражение для первой производной от первого коэффициента T(1):
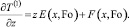
Из граничных условий (17) и (15) при сомножителе ε в первой степени имеем соответственно
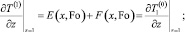
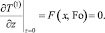 (20)
(20)
Из (20) и (19) найдем уравнение для определения нулевого приближения температурного поля в слое
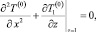
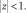 (21)
(21)
Окончательная постановка задачи в нулевом приближении включает также уравнение в окружающей породе
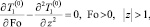 (22)
(22)
а также соответствующие граничные и начальные условия

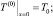 (23)
(23)
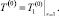 (24)
(24)
Выражения (21)–(24) представляют краевую задачу для нулевого коэффициента разложения T(0) или нулевого приближения.
Для решения задачи воспользуемся интегральным преобразованием Лапласа – Карсона по переменной Fo:
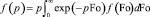 .
.
Математическая постановка искомой задачи в нулевом приближении (21)–(24) в пространстве изображений Лапласа – Карсона по переменной Fo запишется как
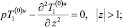 (25)
(25)
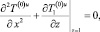
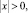
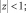 (26)
(26)
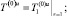
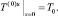 (27)
(27)
Из уравнения (25) с учетом граничного условия (27) и ограниченности на бесконечности получим выражения для 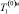 и его производной при z = 1
и его производной при z = 1
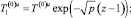
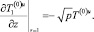 (28)
(28)
С учетом (28) из уравнения (26) получим обыкновенное дифференциальное уравнение для определения T(0)u
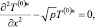 (29)
(29)
откуда, используя условие ограниченности на бесконечности и условие (27), окончательно имеем следующие выражения для решения задачи в пространстве изображений Лапласа – Карсона:
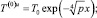
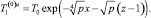 (30)
(30)
Применяя обратное преобразование Лапласа – Карсона, с использованием соотношений [5]
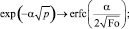
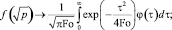
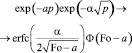 (31)
(31)
получим следующие выражения для точного решения задачи в нулевом приближении:
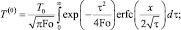
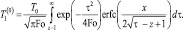 (32)
(32)
В справедливости полученных выражений нетрудно убедиться прямой подстановкой выражений в указанную задачу. Как видно из (32), температура в слое не зависит от вертикальной координаты z и описывает асимптотически осредненные по толщине пласта значения температуры. Найденные выражения (32) определяют пространственно-временные зависимости асимптотически средней температуры пласта в квазистационарном приближении с учетом пространственной анизотропии и нестационарного теплообмена между слоями и могут быть широко использованы для практических расчетов.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор, декан физико-математического факультета, Стерлитамакский филиал Башкирского государственного университета, г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор, заведующий кафедрой алгебры, геометрии и методики обучения математике, Стерлитамакский филиал Башкирского государственного университета, г. Стерлитамак.



