В настоящее время математическое моделирование многих динамических процессов, которые происходят на практике (экономика, промышленное производство, движение самолетов, экология, химия, биология и т.д.), является основным инструментом для получения знаний об их поведении при различных способах воздействия. Одна из главных целей моделирования – найти такое управляющее воздействие, при котором в некотором смысле достигается «максимальный эффект». Например, минимальные затраты ресурсов (денег, времени) на производство единицы продукции или передачи управляемого объекта из начального состояния в заданное конечное состояние.
Наиболее удобные и популярные средства описания динамических процессов – дифференциальные уравнения. Возникающие проблемы, как правило, хорошо известны в теории оптимального управления. Тем не менее подавляющее большинство из них не имеют простого (аналитического) решения и требуют разработки численных методов.
Данная работа посвящена актуальной проблеме – разработке эффективных алгоритмов численного решения задач оптимального управления.
Постановка задачи. Пусть управляемый процесс представлен системой дифференциальных уравнений:
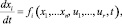(1)
где xi – фазовые переменные, а uj – переменные управления, uj ∈ U.
При t = 0 заданы все начальные значения фазовых переменных xi:
xi(0) = xi0, i = 1, ..., n.. (2)
На управление и фазовые переменные наложены ограничения типа
η(u1, ..., ur) ≤ 0,4; θ(x1, ..., xn) ≤ 0. (3)
Критерий оптимизации пусть задан в терминальном виде
I(x1(T), ..., xp(T)) → min, p ≤ n. (4)
Требуется найти такое управление u(t), удовлетворяющее условиям (3), чтобы величина I(x1(T), ..., xp(T)) приняла минимальное значение.
Алгоритм метода вариации
Для численного решения данной задачи был составлен алгоритм метода вариации в пространстве управлений:
1. Определить первоначальное приближение управления U0 (может быть произвольным).
2. Разбить интервал [t0, tk] на n частей, образующих равномерную систему узлов.
3. Выбрать начальный узел t0, с которым будет происходить вариация управлений.
4. Произвести вариацию в т. t0 в двух направлениях U(t0) ± δU.
5. Решить систему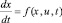 
с начальными условиями x(t0) = x0.
6. Зная значения фазовых координат, вычислить значение критерия I для управления, полученного на шаге 4.
7. Перейти к t1 и повторить процедуру, начиная с шага 4 для всех оставшихся точек ti.
8. Определить наименьшее значение критерия, вычисленных во всех точках ti, и определить новое приближение U1, соответствующее наименьшему значению критерия.
9. С приближением U1 продолжить процедуру с шага 3 до тех пор, пока не найдется ни одной вариации, при которой значение критерия улучшаться не будет.
10. С целью уточнения приближения процесс можно продолжить, поделив вариацию δU пополам.
Тестирование алгоритма
На основе созданного алгоритма реализована программа на языке Object Pascal в среде Delphi. Рассмотрим работу полученного алгоритма на тестовых примерах, при этом для вычисления погрешностей будем использовать евклидову норму вида
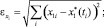
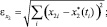
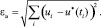
Пример 1
Допустим, что некоторый процесс описывается системой дифференциальных уравнений:
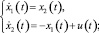(5)
с начальными условиями
x1(0) = 0; x2(0) = 0 (6)
и следующими ограничениями на переменную времени:
0 ≤ t ≤ 2π (7)
и на управление:
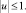(8)
Критерий оптимизации имеет вид
I(x1, x2) = x2(2π) → min. (9)
Требуется найти оптимальное программное управление u*(∙) и соответствующую ему траекторию x*(∙), которые удовлетворяют уравнениям (5)–(6), ограничениям (7)–(8) и условию (9).
Аналитическое решение данной задачи представлено в [2]. На рис. 1, 2 изображено численное решение данной задачи при начальном приближении u0 = 0,3.
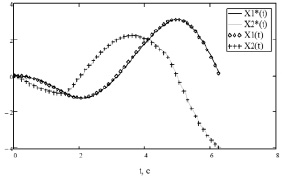
Рис. 1. Графики оптимальных траекторий для примера 1
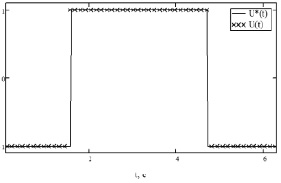
Рис. 2. График оптимального управления для примера 1
Таблица 1
Сравнительный анализ результатов решения задачи 1
|
№ п/п |
u0 |
Точность |
Затраченное время, c |
εu |
|
|
Imin |
|
1 |
0 |
0,1 |
2,06 |
3,06 |
1,11 |
1,21 |
‒3,74 |
|
2 |
0 |
0,01 |
2,85 |
2,99 |
0,14 |
0,15 |
‒3,97 |
|
3 |
0 |
0,001 |
4,12 |
2,987 |
0,018 |
0,019 |
‒3,9949 |
|
4 |
‒0,6 |
0,001 |
3,94 |
2,854 |
0,019 |
0,016 |
‒3,9958 |
|
5 |
‒0,9 |
0,0001 |
12,06 |
2,0024 |
0,1086 |
0,1089 |
‒3,9994 |
|
6 |
0,1 |
0,00001 |
23,35 |
2,0023 |
0,1093 |
0,1088 |
‒3,9997 |
Сравнивая полученные численные и аналитические значения, вычислим погрешности для управления и траекторий. В табл. 1 представлен сравнительный анализ результатов численного решения задачи (5)–(9) при различных значениях начального приближения управления и точности вычислений.
Пример 2
Пусть управляемый процесс описывается системой дифференциальных уравнений:
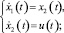(10)
с начальными условиями
x1(0) = –1; x2(0) = 0 (11)
и следующими ограничениями на переменную времени:
0 ≤ t ≤ 2,5 (12)
и на управление, фазовые переменные:
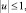x2 ≤ 0,5. (13)
Критерий оптимизации имеет вид
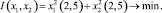(14)
Требуется найти оптимальное программное управление u*(∙) и соответствующую ему траекторию x*(∙), которые удовлетворяют уравнениям (10)–(11), ограничениям (12)–(13) и условию (14).
Аналитическое решение данной задачи представлено в [3]. На рис. 3, 4 изображено численное решение данной задачи, при начальном приближении u0 = 0,1.
Сравнивая полученные численные и аналитические значения, вычислим погрешности для управления и траекторий. В табл. 2 представлен сравнительный анализ результатов численного решения задачи (10)–(14) при различных значениях начального приближения управления, точности вычислений.
Пример 3
Пусть управляемый процесс описывается системой дифференциальных уравнений:
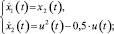(15)
с начальными условиями:
x1(0) = 0; x2(0) = 0 (16)
и следующими ограничениями на переменную времени:
0 ≤ t ≤ 1 (17)
и на управление:
0 ≤ u ≤ 1 (18)
Критерий оптимизации имеет вид
I(x1, x2) = x1(1) → max. (19)
Требуется найти оптимальное программное управление u*(∙) и соответствующую ему траекторию x*(∙), которые удовлетворяют уравнениям (15)–(16), ограничениям (17)–(18) и условию (19).
Аналитическое решение данной задачи представлено в [3].
На рис. 5 изображено численное решение данной задачи при начальном приближении u0 = 0,6. При этом расчетное значение параметра управления на интервале 0 ≤ t ≤ 1 принимает постоянное значение, равное 1.
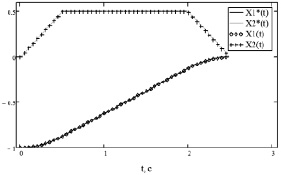
Рис. 3. Графики оптимальных траекторий для примера 2
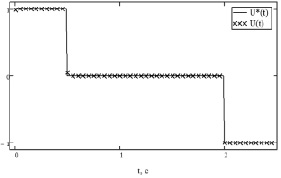
Рис. 4. График оптимального управления для примера 2
Таблица 2
Сравнительный анализ результатов решения задачи 2
|
№ п/п |
u0 |
Точность |
Затраченное время, c |
εu |
|
|
Imin |
|
1 |
0 |
0,1 |
1,12 |
5,46 |
2,97 |
2,58 |
0,15 |
|
2 |
0 |
0,01 |
3,41 |
1,79 |
0,09 |
0,102 |
0,0001 |
|
3 |
0 |
0,001 |
3,95 |
1,807 |
0,088 |
0,102 |
0,0001 |
|
4 |
–0,6 |
0,001 |
4,34 |
1,695 |
0,096 |
0,102 |
0,0001 |
|
5 |
–0,9 |
0,0001 |
7,98 |
1,5092 |
0,0885 |
0,1026 |
0,0001 |
|
6 |
0,1 |
0,00001 |
13,48 |
1,50543 |
0,08875 |
0,10224 |
0,00014 |
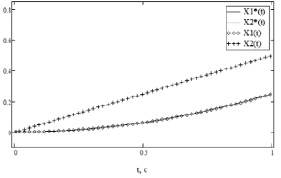
Рис. 5. Графики численного решения примера 3
Таблица 3
Сравнительный анализ результатов решения задачи 3
|
№ п/п |
u0 |
Точность |
Затраченное время, c |
εu |
|
|
Imin |
|
1 |
0,6 |
0,1 |
2,32 |
1,06 |
1,105 |
0,285 |
0,229 |
|
2 |
0,6 |
0,01 |
6,43 |
1,009 |
0,04 |
0,108 |
0,241 |
|
3 |
0,6 |
0,001 |
9,45 |
1 |
0,001 |
0,018 |
0,246 |
|
4 |
0,8 |
0,001 |
11,58 |
1 |
0,003 |
0,009 |
0,247 |
|
5 |
0,8 |
0,0001 |
18,23 |
1 |
0,0033 |
0,0091 |
0,2475 |
|
6 |
0,6 |
0,00001 |
23,85 |
1 |
0,00002 |
0,00007 |
0,24761 |
Сравнивая полученные численные и аналитические значения, вычислим погрешности для управления и траекторий. В табл. 3 представлен сравнительный анализ результатов численного решения задачи (15)–(19) при различных значениях начального приближения управления, точности вычислений.
Заключение
Выполненный сравнительный анализ приближенного и аналитического решения задач показал удовлетворительное согласование и хорошую работу построенного алгоритма. Достоинством данного алгоритма является отсутствие требования к выбору начального приближения параметра управления и фазовых переменных. Алгоритм имеет хорошую сходимость и может быть использован для решения большого класса прикладных задач в различных отраслях народного хозяйства.
Рецензенты:
Муравьева Е.А., д.т.н., профессор, филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Стерлитамак;
Галиев А.Л., д.т.н., профессор, филиал ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Стерлитамак.