Одна из основных тенденций развития машиностроения – это постоянное увеличение производительности механической обработки деталей и повышение точности и качества обработки. При этом для получения высокой производительности применяется высокоскоростное резание, которое как правило сопровождается проявлениями резонанса в элементах технологической системы (ТС) [1–6, 9, 11]. Работа в условиях резонанса не только интенсифицирует износ инструмента, сокращает долговечность элементов системы СПИД, но и приводит к увеличению брака, а также снижению точности и качества обработки. При этом обнаружение частотных зон, в которых вероятно выявление резонансных зон в ТС, весьма затруднено без применения специального оборудования [5, 6].
Рассматриваемый в данной работе подход основан на предварительном моделировании процессов, происходящих в ТС (рис. 1) при обработке заготовки, в результате чего строятся спектральные характеристики элементов ТС, позволяющие определить частотные участки с повышенным уровнем вибрации, тем самым назначить при реальной обработке оптимальные с точки зрения минимального уровня вибрации режимы обработки.
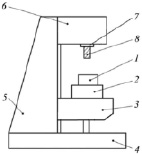
Рис. 1. Компановка ТС: 1 – заготовка; 2 – приспособление; 3 – консольный стол; 4 – основание; 5 – стойка; 6 – шпиндельная бабка; 7 – шпиндель; 8 – инструмент
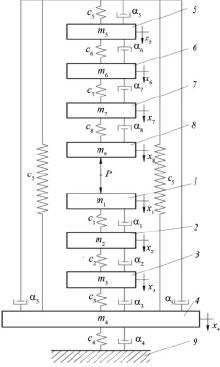
Рис. 2. Расчетная схема ТС: 1–9 – блоки динамической системы; 1 – заготовка; 2 – приспособление; 3 – консольный стол; 4 – основание; 5 – стойка; 6 – фрезерная бабка; 7 – шпиндель; 8 – инструмент; 9 – фундамент
Рассмотрим динамический процесс, возникающий при фрезеровании (рис. 1). ТС представлена в виде дискретной упругомассовой системы (рис. 2), элементы которой описываются массой, коэффициентами жесткости и демпфирования [7].
По расчетной схеме ТС (рис. 2) составляется система дифференциальных уравнений (1), решение которой велось методом Рунге-Кутта четвертого порядка. Обозначения в системе дифференциальных уравнений:
● Р – вертикальная нагрузка, (Н). При моделировании принят гармонический закон изменения возмущающей силы 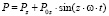 ;
;
● Р0z – амплитудное значение возмущающей силы, имитирующей вертикальную проекцию силы резания (Н);
● Рz – постоянная составляющая вертикальной нагрузки, (Н);
● z – число зубьев фрезы;
● ω (f) – угловая частота (частота), рад/с (Гц);
● t – время, (с);
● m1–8 – массы (кг) элементов ТС (рис. 1);
● x1–8, ẋ1–8, ẍ1–8, – соответствующие узлам (рис. 1, 2) виброперемещения, виброскорости и виброускорения;
● с1–8, α1–8, – соответствующие (рис. 1, 2) узлам коэффициенты жесткости и упругого демпфирования.
Допущение о гармоническом законе действия силы резания принято в данной работе из соображения выявления реакции элементов ТС на такое воздействие, а также факта, что форма сигнала P(t) при спектральном преобразовании будет иметь основную гармонику на указанной частоте ω = z·ωz.
Система линейных неоднородных дифференциальных уравнений:
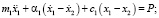
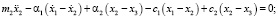
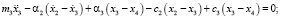
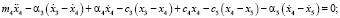
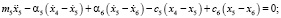
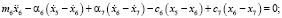
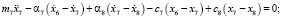
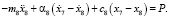
Значения параметров математической модели
|
Масса, Н·с2/м |
m1 |
m2 |
m3 |
m4 |
m5 |
m6 |
m7 |
m8 |
|
4 |
8 |
50 |
220 |
250 |
100 |
35 |
0,2 |
|
|
Коэффициент жесткость, 106 Н/м |
с1 |
с2 |
с3 |
с4 |
с5 |
с6 |
с7 |
с8 |
|
35 |
40 |
45 |
50 |
60 |
80 |
100 |
15 |
|
|
Коэффициент демпфирования, Н с/м |
α1 |
α2 |
α3 |
α4 |
α5 |
α6 |
α7 |
α8 |
|
80 |
100 |
300 |
120 |
100 |
100 |
100 |
70 |
|
|
Амплитудное значение силы, Н |
P0z |
|||||||
|
400 |
||||||||
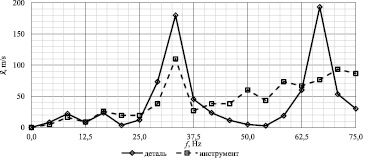
Рис. 3. АЧХ вибросигнала
Значения параметров, вошедших в математическую модель, представлены в таблице. Значения жесткости приняты, опираясь на материалы [8].
По результатам моделирования получены амплитудно-частотные характеристики (АЧХ) элементов ТС (рис. 3).
По результатам (рис. 4) можно выделить две зоны с минимальными значениями уровня вибросигнала:
● в диапазоне от 0 до 25 Гц;
● в диапазоне от 37,5 до 62,5 Гц,
которые можно рекомендовать при назначении режимов технологического процесса, и резонансные частоты, которых следует избегать.
Для сравнения адекватности модели проведено сравнение результатов теоретических (моделирование) и экспериментальных исследований [12] по уровню вибросигнала на заготовке на частоте 25 Гц (рис. 4). Следует отметить, что значения коэффициентов (таблица) при моделировании приняты согласно значениям реальной ТС.
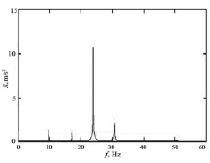
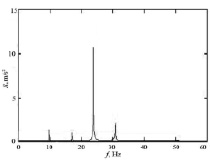
а) б)
Рис. 4. Спектр вибросигнала на заготовке при частоте вращения шпинделя 24 Гц а – теоретические исследования; б – эксперимент, 1–4 – номер зуба фрезы
Уровень вибросигнала по результатам теоретических и практических исследований, соответственно, 10,9 м/с2 и 8,8 м/с2. Таким образом, относительная погрешность исследований составила 19,3 %. Различие результатов теоретических и экспериментальных исследований объясняется тем, что при моделировании:
● принято гармоническое воздействие вместо полигармонического;
● не учитывалась нелинейность реальной ТС.
Таким образом, рассмотренная математическая модель может с достаточной для инженерных расчетов точностью [10] применяться для проведения исследований поведения работающей ТС посредством моделирования процессов, происходящих в ней.
Работа выполнена при поддержке Фонда В. Потанина, исследовательский проект № GK140000513.
Рецензенты:
Нижегородов А.И., д.т.н., профессор, заведующий кафедрой строительных, дорожных машин и гидравлических систем, ФГБОУ ВПО «Иркутский национальный исследовательский технический университет»;
Крауиньш П.Я., д.т.н., профессор кафедры автоматизации и роботизации в машиностроении, ФГАОУ ВПО «Национальный исследовательский Томский политехнический университет».



