При разработке алгоритмов прогнозирования неопределенных параметров по предварительной обучающей выборке на основе принципов нечеткого моделирования [2] возникает задача выбора способа представления исходных данных в виде функции принадлежности для параметров, входящих в обучающую выборку. С этой целью следует каждому измеренному значению связанных параметров из обучающей выборки поставить в соответствие поле распределения информации от отдельного акта измерения – построить аппроксимацию распределения функции принадлежности [3].
Такая же задача возникает и при аппроксимации измеренных данных, по которым ищутся прогнозные значения. Дальнейшая технология прогноза основана на использовании принципа Мамдани для композиции отношений в форме функций принадлежности [4]. Для решения этой задачи необходимо выбрать базисные функции, с помощью которых выполняется заполнение в пространстве значениями информативности от одного отдельно взятого измерения. Естественным выбором в этом вопросе служат два принципа. Во-первых, принимаемое распределение должно иметь максимальную энтропию, что необходимо для того, чтобы не вводить информацию, которой объективно нет. Во-вторых, процесс распространения меры достоверности информации о значении параметра от точки, в которой это значение получено, к точке, в которой эта мера оценивается, должен быть аналогичен диффузии. Это диффузия информации по мере удаления от измеренного объекта. Оказывается, оба эти принципа приводят к одному и тому же результату – выбору аппроксимирующей функции в форме функции Гаусса. Кроме того, между параметрами функции Гаусса, ассоциируемой с дисперсией распределения и параметрами диффузии, существует тесная взаимосвязь, проявляющаяся в совпадении их полугрупповых свойств.
Рассмотрим дифференциальное уравнение:
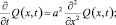(1)
a ≠ 0; –∞ ≤ x ∞; t ≥ 0;
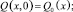
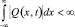
Его решение имеет вид [4]
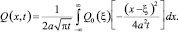(2)
Отсюда, в частности, следует полугрупповое свойство решения уравнения диффузии в однородном пространстве:
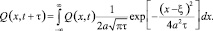(3)
Соотношение (3) представляет собой свертку функций Q(x,t) и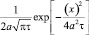 
по переменной x.
Отсюда и из уравнения (1) следует, что если
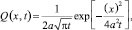(4)
то
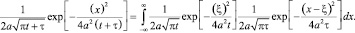(5)
Что сокращенно можно записать
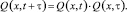(6)
Эти результаты обобщаются на двухмерный и трехмерный случай задачи (1):
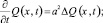x = {x, y, z}; либо x = {x, y}; a ≠ 0; –∞ ≤ x ∞; t ≥ 0; (7)
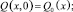
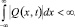
Δ – оператор Лапласа.
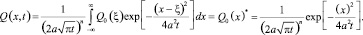(8)
Здесь N – размерность пространства векторов x. Свертка в (8) понимается в пространстве N измерений.
Полагая, что
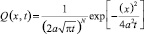, (9)
получаем аналог (5) и (6)
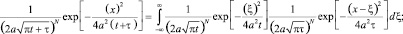(10)
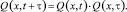
Это равенство может быть записано в форме
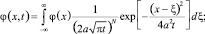(11)
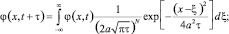
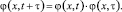
Рассмотрим теперь частный случай соотношения (5).
Запишем
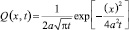
в форме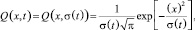 
где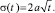 
Тогда, пользуясь соотношением (5), получим
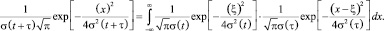(12)
Причем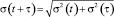 
.
В краткой записи в виде свертки уравнение (12) перепишется:
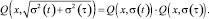(13)
Принимая во внимание представление (2) получим обобщение (13) на произвольную функцию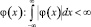 
:
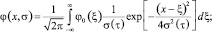(14)
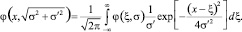
В пространстве двух измерений на основании (8):
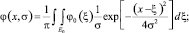(15)
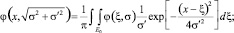
E0 = –∞ ≤ ξ = {ξ1, ξ2} ≤ ∞.
Рассмотрим в N-мерном фазовом пространстве X параметров x = {xi, i = 1...N} экспериментально измеренные значения xj ∈ S; j = 1...M, образующие в нем подмножество A ∈ X. Для поля рассеяния Aε(x) в фазовом пространстве, такого, что для каждой подобласти ΔX из разбиения X:
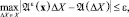(16)
где A(ΔX) – число значений из A ∈ X, целиком лежащее в ΔX, определим функцию принадлежности μA(x) для измеренных значений параметров x ∈ X как нечетких величин, правилом:
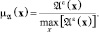
На основании (15) может быть сформулирована задача нахождения распределения источников μ(x, σ) информации для μA(x) как обратной задачи для интегрального уравнения:
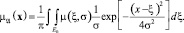(17)
Решение этого интегрального уравнения требует использования методов решения некорректных задач и позволит проанализировать меру рассеяния источников информации в процессе ее движения по измерительному каналу, в котором она подвергалась диффузии.
Выводы
1. Решение уравнения диффузии в однородном бесконечном пространстве с импульсным источником в начальный момент времени для любого другого большего времени совпадает с нормальным законом распределения вероятностей, стандартное уклонение которого возрастает по мере увеличения времени диффузии по правилу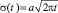 
.
2. Решение уравнения диффузии соответствует распределению с максимальной энтропией при фиксированной скорости и времени диффузии [5], что следует из его совпадения с нормальным законом распределения.
3. Нормальный закон распределения обладает полугрупповыми свойствами относительно дисперсии D(t) = σ2(t):
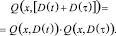(18)
Рецензенты:
Сушков С.И., д.т.н., профессор кафедры технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта;
Павлов А.И., д.т.н., профессор кафедры лесных, деревообрабатывающих машин и материаловедения, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Работа поступила в редакцию 10.04.2015.