Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Важным процессом, определяющим поведение пен и, в частности, их устойчивость, является синерезис. Наиболее полный анализ данного процесса и дифференциальное уравнение синерезиса даны в работах Кротова [1–4]. В работе [1] показано, что коэффициент синерезиса определяется величиной локальной гидропроводности пены HG, которая складывается из гидропроводности каналов и пленок 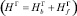. Ее значение известно при условии тангенциальной неподвижности поверхностей пленок и каналов (при большой поверхностной вязкости):

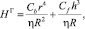(1)

где h – динамическая вязкость; h – толщина пленок (индексы b и f относятся к каналам и пленкам); Cb = 3,6⋅10–4, Cf = 8,8⋅10–2 – гидродинамические коэффициенты, которые определяются геометрическими параметрами каналов и пленок, r – радиус кривизны канала Плато – Гиббса; R – радиус пузырьков. С учетом гидродинамических коэффициентов гидропроводность пены определяется равенством

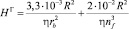. (2)

В работе [1] также показано, что гидропроводность пены носит каналовый характер, если выполняется условие: 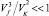, где Vf = 1,64h/R, VK = 0,33r2/R. При этом расход жидкости через пену равен

Q′ = HKrgA, (3)

где А – площадь поперечного сечения пены.

Учитывая объемную долю жидкости в пене

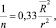
где 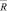 – средний радиус пузырьков в рамках модели ячейки в виде компактного 14-гранника, получим выражение

Q′ = 0,33frgA r2/hn. (4)

Отметим, что уравнение (4) описывает течение дисперсионной среды через пену при выполнении следующих условий: структура пены является полностью полиэдрической; вся жидкость находится в каналах, а содержание жидкости в пленках пренебрежимо мало. Зависимость, подобная уравнению (4), была впервые получена в работе Леонарда и Лемлиха [5] и является аналогом уравнения Пуазейля:

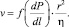(5)

При течении жидкости под действием силы тяжести линейная скорость определяется зависимостью

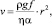(6)

где h – объемная вязкость жидкости. Учитывая влияние поверхностной вязкости (ηs), Нгуйен [6] получил выражение для скорости течения раствора ПАВ по каналу Плато – Гиббса численным решением уравнения Навье – Стокса:

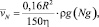(7)

где параметр Ng определяется формулой

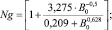(8)

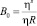 – число Буссинеска. (9)

В работах Десаи и Кумара [7–9] используется величина a, (a = 1/В0), которая называется степенью подвижности поверхностей канала. Зависимость b = f(a) используется в указанных работах для оценки степени подвижности поверхностей.

Методы исследования

1.1. Исследование течения растворов ПАВ

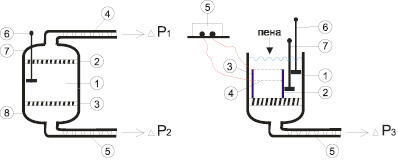
Метод исследования пен под действием приложенных перепадов давления получил название Foam Pressure Drop Technique (FPDT) [10]. Использование пористых керамических или стеклянных пластин позволяет получать «сухие пены» высокой кратности (1000 и более). Исследование течения дисперсионной среды через пену в гравитационном поле и при больших перепадах давлений (DP >> rgH) проводят в ячейках, использованных ранее в работах [11–16] и представленных на рисунке, а, б.

а б

Схемы устройств для исследования течения дисперсионной среды через пену: a – 1 – стеклянная ячейка с двумя пористыми фильтрами; 2, 3 – пористые пластины; 4, 5 – градуированные стеклянные трубки; 6 – микроманометр; 7, 8 – раствор пенообразователя; б – 1 – стеклянная ячейка с пористым фильтром; 2 – стеклянный цилиндр; 3, 4 – электроды; 5 – кондуктометр; 6, 7 – микроманометры; DP1; DP2; DP3 – приложенные к пене перепады давления

Из пеногенератора пена поступает в пеносборник 1 (рисунок, а), ограниченный с двух сторон пористыми перегородками (3, 4). С наружных сторон перегородки находятся в контакте с раствором пенообразователя под одинаковым разряжением DP1 и DP2. Величина приложенного перепада давления (DР) задает радиус каналов Плато – Гиббса:

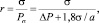(10)

где s – поверхностное натяжение; Рs – капиллярное давление в пене. Отметим, что при больших DР поправкой на капиллярное давление в пузырьках пренебрегали, так как

DР >> 1,8s/а,

где а – дисперсность пены. Объемную скорость раствора (расход) измеряют с помощью градуированных капиллярных трубок (4, 5), когда профиль (изменение радиуса канала по высоте пены) становился равновесным.

Для изучения нестационарного синерезиса пены использовали новый метод с одной пористой пластиной (рисунок, б). Пена помещается в стеклянный стакан (1), дном которого является пористая пластина. На пластину внутри стакана устанавливается стеклянный цилиндр (2) (d = 20 мм) с двумя горизонтальными электродами (3, 4), необходимыми для определения кратности. Электроды представляют собой металлические сетки. На уровне верхнего и нижнего электродов фиксируются два микроманометра (6, 7) для измерения давления в пенных каналах. Стеклянный стакан заполняется пеной (Н = 2 см) перед началом эксперимента, затем под пластиной создается пониженное давление. В течение эксперимента измеряется давление в каналах в нижней и верхней точках пенного столба и электропроводность пены. Важная особенность нового типа метода FPDT с одной пористой пластиной – возможность изучать в каждом эксперименте влияние на скорость синерезиса пены не только радиусов кривизны каналов Плато – Гиббса и объемной доли жидкости, но и градиента давления.

1.2. Измерение капиллярного давления в каналах Плато – Гиббса

Пониженное давление в каналах Плато – Гиббса пены измеряли с помощью капиллярного микроманометра [10]. Микроманометр состоит из тонкого стеклянного капилляра, к нижнему концу которого присоединена пористая пластинка. Капилляр заполняли раствором пенообразователя, а верхнее отверстие капилляра герметично закрывали. Изменяя соотношение объемов воздуха и жидкости в капилляре, можно получить микроманометр для измерения требуемого диапазона давлений. Радиус капилляра был достаточно малым (10–2...2⋅10–2 см), чтобы количество жидкости, вытекающее в пену в результате измерений, было незначительным по сравнению с количеством жидкости в самой пене. Перед началом опыта микроманометр калибровали по образцовому вакуумметру и строили зависимость изменения высоты столбика раствора в капилляре Dh от приложенного перепада давлений DP. Величину приложенного давления (до 104 Па) измеряли водным U-образным манометром с точностью 0,6 %.

Течение дисперсионной среды через пену

В работе [11] в качестве гидродинамической модели пены использовали систему независимых (параллельно соединенных) капилляров, поперечным сечением которых является «сферический» треугольник с постоянным (по длине канала) радиусом кривизны r. Было показано, что скорость течения раствора ПАВ через пену с неизменным по высоте слоя радиусом (r > 50 мкм) канала Плато превышала в 2–9 раз рассчитанную в предположении неподвижной поверхности. Течение раствора ПАВ (при изменении радиуса канала Плато от 30 до 100 мкм) проведено в работах [12–15]. Было изучено течение дисперсионной среды через пену, полученную из раствора ионогенного ПАВ – додецилсульфата натрия (DDSNa) с добавками хлорида натрия или желатины. Отметим, что добавление хлорида натрия в количестве 0,3–0,5 моль/л приводит к формированию в пене черных ньютоновских пленок [10]. Добавление желатины изменяет поверхностную вязкость. Поверхностная вязкость растворов додецилсульфата натрия с добавкой желатины велика и составляет 4,5⋅10–6 и 5–8⋅10–5 Н⋅с/м [16, 17]. В таблице представлено отношение экспериментально полученной (vЭ) скорости течения раствора ПАВ по каналу Плато к теоретической (vТ) в предположении неподвижной поверхности, рассчитанной по уравнению Леонарда – Лемлиха и к скорости течения раствора ПАВ (vN), рассчитанной по формуле (7) с использованием зависимости, предложенной Нгуйеном. Проведено сравнение с теоретической зависимостью b = f(a) Десаи, Кумара.

Оценка степени подвижности поверхности канала Плато – Гиббса

Как видно из таблицы, полную неподвижность поверхностей наблюдали в пенах из DDSNa с ньютоновскими черными пленками (растворы 2, 3) и добавками лаурилового спирта и желатины (растворы 1 и 5). Полную неподвижность поверхностей в этом случае предсказывают теории Десаи, Кумара, Нгуйена (параметр b и отношение vЭ/vN = 1 для растворов 1 и 5, таблица). В растворах DDSNa с ньютоновскими черными пленками, концентрацией электролита 0,334 моль/дм3 и радиусом канала Плато r = 30 мкм полную неподвижность поверхности канала предсказывает зависимость Десаи и Кумара, чему соответствуют экспериментальные данные. Отношение (vЭ/vT = b = 1); при увеличении радиуса канала до 68 мкм vЭ/vT = b = 1,2; vЭ/vN = 1,7. Отметим, что параметр b предсказывает незначительную (в 1,2–1,4 раза) подвижность поверхностей в пенах из раствора DDSNa с обычными черными пленками и в пенах, полученных из неионогенных ПАВ. Однако экспериментальные значения линейных скоростей течения превышали рассчитанные по уравнению Леонарда – Лемлиха в 2–4 раза [11]. Ускоренное (по сравнению с неподвижной поверхностью) течение жидкости по каналам в пенах из раствора Тритона Х-100 и DDSNa с обычными черными пленками, возможно, обусловлено «конвейерным переносом» ПАВ по пленке, контактирующей с каналом Плато [18]. Данный механизм не исключает также вовлечение жидкости, содержащейся в узлах сечения канала в процесс переноса ПАВ. Отношение экспериментальной скорости течения (vэ) к рассчитанной по уравнению Нгуйена (vN) составляет 2,44 и 1,7 в пенах из растворов Тритона Х-100 и DDSNa с обычными черными пленками. В этом случае отношения экспериментальной скорости течения растворов ПАВ к теоретическим значениям, рассчитанным по уравнению Леонарда-Лемлиха, были равны 4,4 и 2,6 соответственно. Отметим, что существуют сложности при использовании уравнения Нгуйена для описания течения растворов ПАВ через пену с радиусами каналов Плато более 100 мкм. Сохраняющиеся в оценке (с помощью уравнения Нгуйена) степени подвижности поверхностей различия могут быть также обусловлены предположением автора о нулевой скорости течения в узлах треугольного сечения канала Плато. Более того, при радиусах каналов более 100 мкм вклад жидкости, содержащейся в узлах и пленках, становится существенным. Исследование нестационарного синерезиса с использованием ячейки, представленной на рисунке, б, проводили в работе [19]. Было показано, что уравнение Леонарда –Лемлиха позволяет описать течение через пену с ньютоновскими черными пленками и радиусами канала Плато менее 40 мкм, полученную из додецилсульфата натрия.

Перспективным (в том числе для изучения течения через пену, стабилизированную твердыми частицами [20, 21]) является исследование нестационарного синерезиса с использованием ячейки, представленной на рисунке, б [19]. Как было показано ранее [19], данный метод позволяет избежать сложного вычисления скорости течения дисперсионной среды через пену при изменяющемся по высоте радиусе канала Плато. В работе [22] уравнение Леонарда – Лемлиха применено для описания течения дисперсионной среды через пену, стабилизированную органомодифицированными частицами гидроксида алюминия. Экспериментальная скорость течения через такую пену совпадает с рассчитанной по уравнению (4) в предположении неподвижной поверхности.

Заключение

Полная неподвижность поверхности канала наблюдается в пенах, полученных из ионогенного ПАВ додецилсульфата натрия (DDSNa) с ньютоновскими черными пленками при радиусе канала 30 мкм, а также в пене из DDSNa с добавкой желатины и лаурилового спирта. Экспериментальная скорость течения через канал Плато в таких пенах совпадает с предсказанной известными теоретическими зависимостями и подтверждает режим течения с доминирующими потерями в каналах.

Кошев А.Н., д.х.н., профессор, Пензенский государственный университет архитектуры и строительства, г. Пенза;

Фокин Г.А., д.т.н., профессор, Пензенский государственный университет архитектуры и строительства, г. Пенза.

Работа поступила в редакцию 18.03.2015.