Приоритетом предприятия, функционирующего в рыночной среде, является стремление к росту целевых показателей деятельности. Эта аксиома отражена в известных «моделях развития», в которых заложен принцип динамического соответствия рыночной деятельности предприятия с внешней средой, в границах которой происходит обмен материальными, финансовыми и информационными потоками. Конкретная модель описывает возможные направления и динамику основных сфер этой деятельности (производственной, инвестиционной и финансовой) относительно выбранной миссии и сформулированных целей [2, 3, 4, 5]. В рамках такого подхода необходима трансформация или даже смена модели развития в случае нарушения равновесного состояния в паре «предприятие – внешняя среда».
Приведем классификацию моделей развития в соответствии с работой [4] (таблица).
Первая группа моделей связана с ростом масштаба производства (основная производственная деятельность). Стратегическая направленность этих моделей связана с укреплением конкурентных позиций предприятия на товарных рынках. Варьируемыми показателями являются номенклатурный и объемный составы производственной программы.
Вторая группа моделей ориентирована на рост бизнеса за счет расширения видов деятельности, напрямую не связанных с миссией предприятия. Стратегическая направленность моделей этой группы связана с обеспечением экономической безопасности и мобильности предприятия на основе синергетического эффекта и снижения производственного риска. Варьируемым показателем является уровень диверсификации основного производства.
Модели экономического развития предприятия
|
I группа |
II группа |
||
|
Стратегическая направленность |
Повышение конкурентоспособности предприятия |
Повышение экономической безопасности предприятия |
|
|
Факторы роста |
Экстенсивные |
Интенсивные |
Экстенсивные + Интенсивные |
|
Основные эффекты |
Масштаб производства |
Масштаб производства и рыночная эффективность |
Синергетический эффект + снижение производственного риска |
|
Целевая направленность и критерии |
Рыночная эффективность, длительность цикла «производство + реализация» |
Совокупные издержки, уникальность продукции, престиж на рынке |
Уровень диверсификации производственно-коммерческой деятельности |
Рассмотрим проблематику разработки моделей первой группы, связанных с планированием развития предприятия в условиях отказа от коренной реконструкции и остановки основного производства. Пусть производственная система (ПС) предприятия включает n отдельных производственных комплексов (ПК). Технологическая взаимосвязь комплексов состоит в том, что общая производственная мощность предприятия определяется мощностью самого «слабого звена», т.е. соответствует минимальной мощности входящих в технологическую цепочку комплексов. Категория «мощность» соответствует выходу ПС и увязана с результатами основной производственной деятельности [1]. В экстенсивных моделях фактором роста является масштаб производства, определяемый с производственно-технологическим потенциалом (ПТП) как всего предприятия, так и входящих в него отдельных ПК.
Производственная устойчивость предприятия оценивается накопленным потенциалом устойчивого развития и в первой группе моделей может быть описана величиной производственного риска. Взаимосвязанный с ростом производственно-технологического потенциала рост масштаба производства приводит к снижению производственного риска как всего предприятия, так и отдельных ПК, входящих в его структуру.
Необходимо сделать следующее замечание. Наряду с производственным риском, интерпретируемым как риск потери производственной устойчивости в результате снижения объемов производства и реализации продукции[1], в модели экономического развития целесообразно также рассматривать и технологический риск, связанный с нарушением технологического и производственного циклов по причинам выхода из строя или сбоев в работе основного технологического оборудования (ОТО). Этот вид рисков может быть оценен как вероятность отказов или сбоев в работе ОТО в течение полного производственного цикла или, напротив, времени функционирования i-го ПК.
Рассмотрим временной аспект реализации рыночной стратегии предприятия. Пусть в начальный момент времени i-й ПК 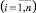 обладает
обладает 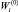 -м уровнем ПТП, который обеспечивает
-м уровнем ПТП, который обеспечивает 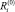 -й уровень технологического риска для i-го ПК. Повышение ПТП i-го ПК до уровня
-й уровень технологического риска для i-го ПК. Повышение ПТП i-го ПК до уровня 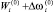 обеспечивает снижение технологического риска до величины
обеспечивает снижение технологического риска до величины 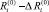 .
.
При построении планов увеличения ПТП отдельных ПК необходимо выбрать уровни организационно-технических мероприятий по реструктуризации и модернизации ПС этих комплексов и сроки их проведения. В качестве критериев можно рассматривать следующие [4]:
а) величина технологического риска всей ПС, обеспечиваемая в процессе реализации соответствующего плана, которая, таким образом, характеризует существующий уровень этого риска для всех входящих в производственную систему ПК;
б) масштаб производства и накопленный ПТП, характеризующие темп снижения показателей производственного и технологического рисков за период реализации плана.
На рисунке показана взаимосвязь этих показателей для конкретных траекторий, характеризующих различные рыночные стратегии наращивания ПТП предприятия.
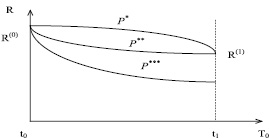
Траектории, характеризующие планы повышения ПТП предприятия
На рисунке приведены начальные и конечные значения показателя технологического риска для трех планов увеличения ПТП некоторого ПК. План P** предпочтительнее плана P* т.к., обеспечивая равный с P* конечный риск, позволяет увеличить объем производства для всей ПС (площадь под кривой P* больше площади под кривой P**, а следовательно, первый план обеспечивает меньшее время бессбойной работы всей ПС, чем второй). План P***, в свою очередь, предпочтительнее плана P**, т.к. имеет лучшие характеристики по обоим показателям.
В систему ограничений моделей экономического развития следует включить объемы ресурсного обеспечения M, выделяемые на развитие ПС предприятия и дифференцированные по отдельным периодам (годам).
Содержательную постановку задачи оптимизации можно сформулировать следующим образом: необходимо сформировать план увеличения ПТП отдельных производственных комплексов ПС, обеспечивающий при выделенных объемах ресурсного обеспечения достижение минимально возможных показателей технологического риска в конце периода планирования и максимально быстрое наращивание объемов производства в течение этого периода: 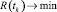 ;
; 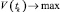 при m ≤ M, где tk – последний интервал планирования.
при m ≤ M, где tk – последний интервал планирования.
Рассмотрим формальную постановку задачи. Пусть i 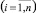 – номер ПК; λi(t) – прогнозируемая величина времени функционирования i-го ПК в интервале t;
– номер ПК; λi(t) – прогнозируемая величина времени функционирования i-го ПК в интервале t; 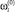 – начальный объем производства i-го ПК.
– начальный объем производства i-го ПК.
«Прирост» показателя уровня технологического риска Ri, обусловленный приростом производственно-технологического потенциала Δωi i-го ПК, задается соотношением
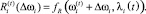 (1)
(1)
За период t на i-м ПК обеспечивается увеличение потенциала производственной системы:
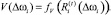 (2)
(2)
Управляемое изменение показателей Ri и Vi i-го ПК требует соответствующих затрат ресурсного обеспечения. Обозначим эти затраты 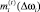 (затраты на закупку, установку и эксплуатацию основного и вспомогательного технологического оборудования).
(затраты на закупку, установку и эксплуатацию основного и вспомогательного технологического оборудования).
В качестве интегральной характеристики технологического риска примем уровень надежности ПС:
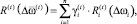 (3)
(3)
где 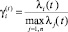 – доля времени функционирования i-го ПК в общем времени функционирования ПС в периоде t.
– доля времени функционирования i-го ПК в общем времени функционирования ПС в периоде t.
Аналогично совокупный объем производства для ПС может быть рассчитан по формуле
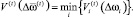 (4)
(4)
Затраты на наращивание ПТП производственной системы в периоде t суммируются по отдельным ПК:
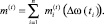 (5)
(5)
План развития ПС заключается в определении вектора 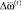 . Вектор
. Вектор 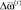 назовем допустимым, если m(t) ≤ Mt, где Mt – объем ресурсного обеспечения, выделяемый на развитие ПС в периоде t.
назовем допустимым, если m(t) ≤ Mt, где Mt – объем ресурсного обеспечения, выделяемый на развитие ПС в периоде t.
Рассмотрим функцию управления:
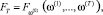 (6)
(6)
где T – количество интервалов планирования; 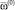 – начальный уровень надежности ПС;
– начальный уровень надежности ПС; 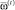 – допустимый план в t-м интервале планирования
– допустимый план в t-м интервале планирования 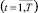 .
.
Сформулируем задачу выбора оптимального управления. Необходимо построить функцию FT управления развитием ПС на отрезке [1, T], обеспечивающую минимум технологического риска ПС и максимум результата производственной деятельности: 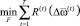 и
и 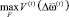 , где min и max берутся по всем возможным управлениям с допустимыми по ресурсному обеспечению планами:
, где min и max берутся по всем возможным управлениям с допустимыми по ресурсному обеспечению планами:
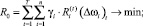 (7)
(7)
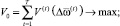 (8)
(8)
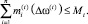 (9)
(9)
Задача (7)–(9) – двукритериальная оптимизационная задача. Как следует из содержательной постановки задачи, критерии являются равноценными. Однако приведенная на рисунке иллюстрация показывает, что лучшим управлением, обеспечивающим заданный уровень технологического риска, является то, у которого траектория выше, что характеризует уже масштаб производства. В силу соотношений (1) и (2) функционал модели нелинеен. Задача линейна лишь по ограничению по затратам и относится к классу задач дискретной оптимизации большой размерности. Для перевода модели на уровень канонического представления задачи дискретной оптимизации необходимо фактор времени ввести в модель явно. Сделаем это в форме символа Кронекера:
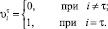 (10)
(10)
Будем считать первой компонентой функции управления, относящейся к периоду планирования τ, вектор 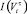 , компонентами которого, в свою очередь, являются номера производственных комплексов, по которым при данном управлении планируется увеличение ПТП.
, компонентами которого, в свою очередь, являются номера производственных комплексов, по которым при данном управлении планируется увеличение ПТП.
Если 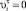 , то значение показателя
, то значение показателя 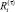 в (3) равно
в (3) равно 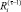 – технологический риск в периоде τ – 1. Иначе,
– технологический риск в периоде τ – 1. Иначе, 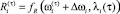 (соотношение (1)). Аналогично, если
(соотношение (1)). Аналогично, если 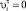 , то значение
, то значение 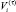 в (4) равно
в (4) равно 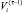 – объем производства в периоде τ – 1, а иначе,
– объем производства в периоде τ – 1, а иначе, 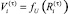 (соотношение (2)).
(соотношение (2)).
Дальнейшая дискретизация задачи связана с моделированием динамики, задаваемой соотношениями (1) и (2).
Будем считать, что
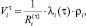 (11)
(11)
где λi(τ) – ожидаемое время загрузки i-го ПК в периоде τ;
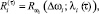 (12)
(12)
где 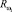 – прямоугольная матрица величин снижения технологического риска с достигнутого уровня ωi;
– прямоугольная матрица величин снижения технологического риска с достигнутого уровня ωi; 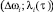 – элемент матрицы показателей объема производства, соответствующего Δωi, и времени загрузки i-го ПК, соответствующего λi(τ); ρi – коэффициент пересчета нормо-часов загрузки i-го ПК в производственную мощность ПК.
– элемент матрицы показателей объема производства, соответствующего Δωi, и времени загрузки i-го ПК, соответствующего λi(τ); ρi – коэффициент пересчета нормо-часов загрузки i-го ПК в производственную мощность ПК.
С учетом соотношений (10)–(12) задачу оптимального управления реструктуризацией ПС предприятия запишем в виде
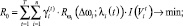 (13)
(13)
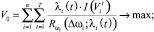 (14)
(14)
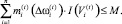 (15)
(15)
В функционалах (13) и (14) поменяем местами суммирование:
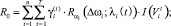 (13’)
(13’)
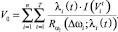 (14’)
(14’)
Эти формальные действия позволяют трансформировать полученную задачу дискретного программирования в задачу с булевыми переменными переборного типа.
Действительно, рассмотрим план увеличения ПТП i-го ПК во времени:
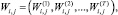 (16)
(16)
где j – номер плана переоснащения i-го ПК.
Каждому плану Wi,j на промежутке [1, T] соответствует конкретное значение 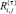 технологического риска. Функцию управления F зададим в виде булевой функции, поставив в соответствие каждому альтернативному варианту управления Wi,j булеву переменную Pi,j = {0; 1}. При Pi,j = 1 из множества всех возможных вариантов управления (16) выбирается именно это управление. Условие выбора только одного варианта управления Wi,j:
технологического риска. Функцию управления F зададим в виде булевой функции, поставив в соответствие каждому альтернативному варианту управления Wi,j булеву переменную Pi,j = {0; 1}. При Pi,j = 1 из множества всех возможных вариантов управления (16) выбирается именно это управление. Условие выбора только одного варианта управления Wi,j:
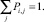 (17)
(17)
Таким образом, дискретную модификацию оптимизационной задачи (7)–(9) можно сформулировать следующим образом. Найти значения булевых переменных Pi,j, обеспечивающих экстремумы функционалам R0 и V0:
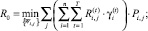 (18)
(18)
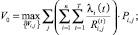 (19)
(19)
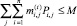 (20)
(20)
при дополнительном условии (17).
Задача (17)–(20) – задача дискретного программирования в булевых переменных. Ее можно классифицировать как многомерную задачу о ранце с критериями (18) и (19).
Решение задачи (17)–(20) может быть получено с использованием метода определения эффективных по Парето планов. Введем понятие оптимального по Парето решения. Обозначим множество допустимых управлений Fg. Эффективным по Парето называется такое управление F* ∈ Fg, что для любого F ∈ Fg неравенства V(F) ≥ V0(F*), R0(F) ≤ R0(F*) могут одновременно выполняться только в случае, если V(F) = V0(F*) и R0(F) = R0(F*). Множество управлений F* называют множеством Парето, а управление F* – вектором Парето.
В теории принятия решений за основу взят принцип: в качестве возможных решений следует выбирать те, которые принадлежат множеству Парето. При этом не выделяется единственное решение экстремальной задачи, но множество альтернативных решений сужается до множества, содержащего только неулучшаемые эффективные решения. Окончательный выбор при этом остается за лицом, принимающим решения (ЛПР). Определение множества Парето существенно облегчает процедуру выбора.
Рассмотрим метод определения решений, оптимальных по Парето, который основан на утверждении, что для двукритериальной линейной задачи решения, оптимальные по Парето, являются единственными (с точностью до равенства на них R0 и V0) решениями однокритериальных задач (18), (20), (17) или (19), (20), (17), если в последние добавить ограничения
V(F) ≥ V*,
где 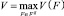 (21)
(21)
или
R(F) ≤ R*,
где 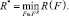 (22)
(22)
Решения, оптимальные по Парето, определяются по следующему алгоритму:
а) находится оптимальное решение задачи (18), (20), (17) и определяются 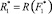 и
и 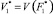 , где
, где 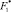 – соответствующее оптимальное управление;
– соответствующее оптимальное управление;
б) находится решение задачи (19), (20), (17) и определяется 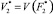 , где
, где 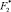 – соответствующее оптимальное управление;
– соответствующее оптимальное управление;
в) формируется интервал 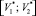 ;
;
г) решается семейство задач (18), (20), (17) с дополнительными ограничениями V(F) ≥ β для различных β из интервала 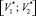 . Из полученных решений выбираются неулучшаемые вектора, которые и составляют управления, оптимальные по Парето.
. Из полученных решений выбираются неулучшаемые вектора, которые и составляют управления, оптимальные по Парето.
Предлагается следующий алгоритм поиска неулучшаемого управления в задаче с критерием на минимум суммарного технологического риска элементов ПС. На следующем этапе схема данного алгоритма может быть использована в процедуре второго шага алгоритма определения управлений, оптимальных по Парето.
Итак, рассмотрим задачу (18), (20), (17):
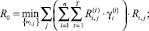
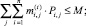
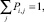
где 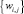 – множество допустимых планов увеличения ПТП i-го ПК.
– множество допустимых планов увеличения ПТП i-го ПК.
Алгоритм поиска квазиоптимального решения рассматриваемой задачи использует ее «рюкзачную» специфику и основан на динамической процедуре «сворачивания» наилучшего плана, не являющегося допустимым, до «уровня» допустимого.
Пусть 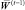 – план увеличения ПТП комплексов ПС, использованный в интервале планирования (t – 1).
– план увеличения ПТП комплексов ПС, использованный в интервале планирования (t – 1).
Определение 1. Глубиной плана 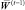 по i-й компоненте плана назовем величину
по i-й компоненте плана назовем величину 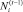 – количество различных планов увеличения ПТП i-го ПК с достигнутого уровня
– количество различных планов увеличения ПТП i-го ПК с достигнутого уровня 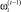 .
.
Определение 2. Весом плана 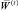 по i-й компоненте назовем величину
по i-й компоненте назовем величину 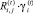 .
.
Определение 3. Весом плана 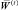 назовем наибольший по всем n компонентам вес.
назовем наибольший по всем n компонентам вес.
Пусть
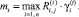 (23)
(23)
Приведем алгоритм поиска квазиоптимального решения задачи (18), (20), (17).
1. Рассмотрим план повышения надежности функционирования элементов ПС, при котором по каждому ПК достигается наименьший уровень показателя технологического риска. В этом случае уровень надежности i-го ПК 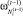 . (Считаем, что планы перенумерованы в последовательности увеличения объема производства). Ясно, что функционал (18) принимает наименьшее возможное значение (что соответствует наименьшему возможному значению веса).
. (Считаем, что планы перенумерованы в последовательности увеличения объема производства). Ясно, что функционал (18) принимает наименьшее возможное значение (что соответствует наименьшему возможному значению веса).
Проверим выполнение условия (21). Если условие выполняется, то получено оптимальное решение задачи для интервала t. Это решение совпадает с вектором 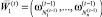 . Иначе переходим к шагу 2.
. Иначе переходим к шагу 2.
2. В плане 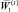 отметим те комплексы, вес которых соответствует весу плана
отметим те комплексы, вес которых соответствует весу плана 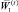 , а среди этих комплексов, в свою очередь, выделим те, глубина которых максимальна. Для этих комплексов рассмотрим последовательно планы, в которых глубина сокращается на единицу, затем на две единицы и т.д. до тех пор, пока вновь полученный план не станет допустимым (удовлетворяющим условию (20)). В этом случае полученный план будет квазиоптимальным решением задачи (18), (20), (17).
, а среди этих комплексов, в свою очередь, выделим те, глубина которых максимальна. Для этих комплексов рассмотрим последовательно планы, в которых глубина сокращается на единицу, затем на две единицы и т.д. до тех пор, пока вновь полученный план не станет допустимым (удовлетворяющим условию (20)). В этом случае полученный план будет квазиоптимальным решением задачи (18), (20), (17).
Если все рассматриваемые планы остаются в области недопустимых, то в плане 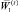 обязательно найдется такая компонента с некоторым номером j0, которая не была включена в первоначальный список.
обязательно найдется такая компонента с некоторым номером j0, которая не была включена в первоначальный список.
Обозначим промежуточный план 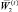 .
.
Повторим итеративную процедуру п. 2, поменяв план 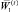 на план
на план 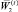 .
.
В силу конечности множества допустимых планов приведенный алгоритм является сходящимся.
Рассмотренный алгоритм позволяет находить квазиоптимальное решение оптимизационной задачи на конкретном интервале планирования. Однако он не решает общей задачи оптимизации планов увеличения ПТП производственной системы на длительном промежутке времени. Для этой цели может быть использована динамическая процедура Р. Беллмана. Обозначим оптимальные по критериям R и V планы соответственно 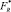 и
и 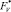 . Разобьем период планирования на l годовых отрезков и соответственно план F на l векторов таких, что
. Разобьем период планирования на l годовых отрезков и соответственно план F на l векторов таких, что 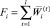 , где каждый вектор
, где каждый вектор 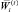 представляет собой годовой план на отрезке (t – 1, t).
представляет собой годовой план на отрезке (t – 1, t).
В соответствии с динамической процедурой Р. Беллмана будем решать l порожденных задач, генерируя ограничения t-й задачи по результатам решения (t – 1)-й. В этом случае может быть получено единственное оптимальное решение всей задачи по двум критериям R и V.
Однако принцип Беллмана справедлив, если в каждой точке траектории множество 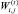 допустимых управлений одинаково. По мере решения порожденных задач и выбора соответствующих управлений на предыдущих шагах, это множество сокращается. Действительно, если в выражении (17) Рi,j для некоторого периода t равно 1, то данное мероприятие плана уже фиксировано. Чтобы снять это возражение, необходимо рассматривать решение порожденных задач в обратном порядке, т.е. от конечной точки плана l к начальной 1. В этом случае первой решается задача с ограничением
допустимых управлений одинаково. По мере решения порожденных задач и выбора соответствующих управлений на предыдущих шагах, это множество сокращается. Действительно, если в выражении (17) Рi,j для некоторого периода t равно 1, то данное мероприятие плана уже фиксировано. Чтобы снять это возражение, необходимо рассматривать решение порожденных задач в обратном порядке, т.е. от конечной точки плана l к начальной 1. В этом случае первой решается задача с ограничением 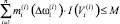 и при этом определяется оптимальное конечное состояние системы
и при этом определяется оптимальное конечное состояние системы 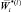 , а затем генерируются и решаются задачи определения управлений по критерию
, а затем генерируются и решаются задачи определения управлений по критерию 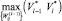 , при ограничениях на
, при ограничениях на 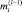 , соответствующих интервалу планирования l–1, что позволяет найти оптимальное для периода l–1 решение.
, соответствующих интервалу планирования l–1, что позволяет найти оптимальное для периода l–1 решение.
С учетом изложенного алгоритм решения динамической задачи (17)–(20) может быть представлен следующим образом.
Пусть i-й ПК в начальный момент периода планирования обладает 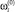 -м масштабом производства. Из анализа ресурсных характеристик оборудования, эксплуатируемого на комплексе, устанавливаются плановые сроки его замены. Для времени замены можно сформулировать несколько вариантов наращивания объема производства. Пусть
-м масштабом производства. Из анализа ресурсных характеристик оборудования, эксплуатируемого на комплексе, устанавливаются плановые сроки его замены. Для времени замены можно сформулировать несколько вариантов наращивания объема производства. Пусть  предусматривает сохранение начального уровня, т.е. замену оборудования, отработавшего ресурс, оборудованием этого же типа. Вариант
предусматривает сохранение начального уровня, т.е. замену оборудования, отработавшего ресурс, оборудованием этого же типа. Вариант 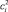 – наращивание объема производства до
– наращивание объема производства до 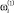 и т.д. Последний вариант
и т.д. Последний вариант 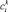 предусматривает вывод объема производства i-го ПК на нормативный уровень
предусматривает вывод объема производства i-го ПК на нормативный уровень 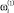 .
.
С учетом располагаемого ресурса технологического оборудования определяется следующий плановый срок его замены и в новой временной точке для каждого варианта  формируется в соответствующих пределах вариант переоснащения и т.д. (до конца l-го интервала планирования).
формируется в соответствующих пределах вариант переоснащения и т.д. (до конца l-го интервала планирования).
Если объем производства, обеспечиваемый i-м ПК, предельно низок, то дооснащение может быть проведено в любой точке периода планирования, независимо от остаточного ресурса финансового обеспечения.
В результате для каждого ПК формируется множество альтернативных планов:

На множестве ci существует несколько альтернативных планов, предусматривающих один и тот же конечный объем производства для i-го ПК, но различные уровни увеличения ПТП в течение всего периода планирования. Эти планы обеспечивают одинаковую конечную эффективность функционирования ПС, но различную эффективность по периодам планирования.
Рассмотрим процесс реализации плана ci. На отрезке времени (0, t1) i-й ПК обеспечивает объем производства 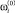 и соответствующие показатели эффективности
и соответствующие показатели эффективности 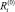 и
и 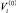 . В момент t1 происходит наращивание уровня ПТП-го комплекса, что обусловливает уменьшение технологического риска на
. В момент t1 происходит наращивание уровня ПТП-го комплекса, что обусловливает уменьшение технологического риска на 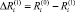 . До момента времени t2 этот прирост обусловит соответствующий вклад в критерий V:
. До момента времени t2 этот прирост обусловит соответствующий вклад в критерий V:
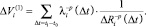 (24)
(24)
Естественно, что на отрезке [t1, t2] можно рассматривать линейную экстраполяцию функций λi и Ri, определяя средние значения 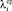 и
и 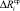 .
.
Далее, в момент времени t2 происходит очередное наращивание ПТП, что обусловливает соответствующее уменьшение технологического риска 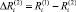 на отрезке времени t2 – t1.
на отрезке времени t2 – t1.
Для каждого плана ci можно определить соответствующие значения 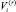 как
как
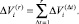
В то же время для плана ci можно определить вклад в критерий R:
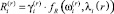
Тогда каждый альтернативный план характеризуется оценками 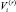 и
и 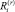 . Запишем оценки, соответствующие плану
. Запишем оценки, соответствующие плану  , в виде
, в виде
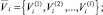
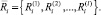
План ci характеризуется потребными для его реализации затратами 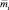 . Учитывая, что ограничения на развитие ПТП производственной системы задаются на интервалах
. Учитывая, что ограничения на развитие ПТП производственной системы задаются на интервалах 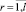 периода планирования, сформируем соответствующие векторы затрат на реализацию альтернативных планов:
периода планирования, сформируем соответствующие векторы затрат на реализацию альтернативных планов:
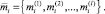
С учетом изложенного процедура нахождения планов, оптимальных по Парето, выглядит следующим образом.
Определяется план ci, имеющий при назначенных ограничениях на вектор затрат mi большую эффективность по критерию R:
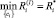 .
.
Среди планов, имеющих такую же конечную эффективность, выбирается план, обеспечивающий больший объем производства. Исходя из полученного плана, строится план для интервала планирования (tl–1, tl), у которого в качестве критерия рассматривается показатель R, а новым ограничением выступает 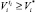 , где
, где 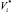 – объем производства, полученный на предыдущем шаге.
– объем производства, полученный на предыдущем шаге.
Вычисляется новое значение 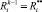 . Среди планов, имеющих такую же эффективность на предпоследнем интервале планирования, выбирается план, обеспечивающий наибольший показатель
. Среди планов, имеющих такую же эффективность на предпоследнем интервале планирования, выбирается план, обеспечивающий наибольший показатель 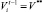 объема производства, и далее процедура продолжается к первому интервалу планирования.
объема производства, и далее процедура продолжается к первому интервалу планирования.
Рецензенты:
Тихомиров Н.П., д.э.н., заведующий кафедрой «Математические методы в экономике», РЭУ им. Г.В. Плеханова, г. Москва;
Титов В.А., д.э.н., профессор кафедры информационных технологий, РЭУ им. Г.В. Плеханова, г. Москва.
Работа поступила в редакцию 02.03.2015.
[1] Приведенное более широкое толкование производственного риска позволяет конкретизировать причины возникновения данного вида риска, последствиями которого является снижение объемов производства и реализации продукции. К ним следует отнести: снижение производительности труда, простои оборудования, потери рабочего времени, отсутствие необходимого количества исходных материалов, повышенный процент брака; снижение цен, по которым планировалось реализовывать продукцию или услугу, в связи с ее недостаточным качеством, неблагоприятным изменением рыночной конъюнктуры, падением спроса; увеличение материальных затрат в результате перерасхода материалов, сырья, топлива, энергии, а также за счет увеличения транспортных и торговых издержек, накладных и побочных расходов; рост фонда оплаты труда за счет превышения численности либо за счет выплат более высокого, чем запланировано, уровня заработной платы отдельным сотрудникам; увеличение налоговых платежей и других отчислений в результате изменения ставки налогов в неблагоприятную сторону; низкую дисциплину поставок, перебои с топливом и электроэнергией; физический и моральный износ оборудования.



