Сточные воды ряда отраслей промышленности (химической, фармацевтической, металлургической, целлюлозно-бумажной, горно-перерабатывающей и др.) вносят значительный вклад в загрязнение поверхностных и подземных водных объектов фенольными и трудноокисляемыми органическими соединениями. Фенол – потенциально опасное, канцерогенное вещество, представляющее значительную медицинскую проблему, даже при низких концентрациях.
Усовершенствованные окислительные процессы (AOP) играют важную роль в разложении органических веществ, содержащихся в сточных водах в широких пределах концентраций. AOP-процессы генерируют гидроксильные радикалы, которые являются сильными окислителями, способными осуществлять минерализацию широкого спектра органических веществ. Гидроксильный радикал имеет высокий окислительно-восстановительный потенциал (E0 = 2,80 В) и способен реагировать с фактически всеми классами органических соединений [4]. Окисляющие гидроксильные радикалы могут быть инициированы фотолизом в результате фото-Фентон процесса.
Очистка сточных вод от фенольных соединений с использованием усовершенствованных окислительных процессов происходит преимущественно в фотохимических реакторах. Фотохимические реакторы, представляют собой аппараты, в которых осуществляются фотохимические реакции. Но в них не только совершаются превращения, но и протекают сопутствующие процессы массо- и теплообмена и интенсивное движение среды. От правильности выбора типа реактора, его конструкции и режима работы в наибольшей степени зависит эффективность и безопасность процесса очистки [6].
При использовании фотореакторов для решения различных прикладных задач эффективному облучению в них должны подвергаться большие объемы реагентов.
Важным элементом модуля фотохимической очистки в общей системе локальных очистных сооружений является система дозирования реагентов, катализатора FeCl3 и перекиси водорода Н2О2.
Для стабильного функционирования реакторов и повышения эффективности минерализации органических соединений необходима оптимизация процесса очистки с целью определения оптимальных доз реагентов, вводимых в реактор. Оптимизация может быть основана на минимизации затрат, требуемых для осуществления запаса реагентов с учетом экологического регулирования процесса очистки. В качестве экологического регулятора может выступать функция зависимости концентрации органического загрязнителя от параметров процесса (концентраций реагентов и времени УФ-облучения), ограниченная предельно допустимым значением концентрации фенольного соединения. Функция концентрации определяется на основе статистического анализа экспериментальных данных АОР-процесса методом наименьших квадратов (МНК).
Зачастую задача определения параметров регрессионного уравнения методом наименьших квадратов является некорректно поставленной, и использование полученного уравнения при решении задачи оптимизации по определению оптимальных доз реагентов может привести к неадекватным результатам.
Таким образом, целью работы является применение методов регуляризации к построению устойчивой модели зависимости концентрации фенольного соединения от параметров процесса фотохимической очистки и идентификации оптимальных уровней расходов перекиси водорода и хлорида железа (III) при минимизации затрат на реагенты.
Для построения математической модели зависимости снижения концентрации фенольного соединения от параметров АОР-процесса при совместном воздействии перекиси водорода, хлорида железа (III) и ультрафиолетового излучения длиной волны 365 нм на фенольный загрязнитель в водной среде с целью решения задачи оптимизации по идентификации уровней расходов химических реагентов проводились экспериментальные исследования на модельных растворах, содержащих фенольные соединения (бисфенол-А, ВРА), с применением жидкостной и газовой хроматографии. При проведении оптимального планирования эксперимента оценивалось влияние УФ-излучения и окислителей на уровень разложения органического загрязнителя при различных концентрациях ВРА – x1 (50 мкг/л, 100 мкг/л); перекиси водорода H2O2 – x2 (100 мг/л; 200 мг/л) и активатора – хлорида железа (III) FeCl3 (1; 2 г/л) – x3. Модельный раствор, содержащий ВРА, перекись водорода и FeCl3, подвергался воздействию УФ-излучения в течение 2 часов (время облучения t – x4). Пробы отбирались через 1 и 2 часа после облучения, и измерялась остаточная концентрация ВРА (y). Измерения осуществлялись жидкостным хроматографом LC-MS/MS. Продукты полураспада в течение фотодеградации ВРА были определены с помощью газового хроматографа GS-MS [8, 9].
При реализации процесса фото-Фентона (Fe2+/Н2О2/hν) для минерализации органических загрязнителей в кислой среде при рН = 3, формируется комплекс Fe(OH)2+ [4, 11, 17]:
Fe 2+ + H2O2 → Fe 3+ + OH● + OH−;
Fe 3+ + H2O → Fe(OH) 2+ + H+.
Под действием УФ-облучения комплекс подвергается разложению, в результате чего образуются радикал OH● и ион Fe2+ :
[Fe(OH)] 2+ + hν → Fe 2+ + OH●.
Количественное описание фото-Фентон процесса на макроуровне, применительно к деградации органического загрязнителя в водной среде, можно описать моделью [18]:
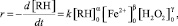
где [RH]0 – начальная концентрация органического загрязнителя; [Fe2+ ]0, [H2O2]0 – начальные концентрации, активатора, содержащего ионы железа (II) и перекиси водорода соответственно; k – константа скорости реакции; r – скорость реакции; α, β, γ – порядки реакции по веществам.
При создании математической модели зависимости снижения концентрации фенольного соединения, от факторов процесса фотохимической очистки с участием реагента «фото-Фентона» будем исходить из линейных моделей или моделей, которые можно свести к линейным по коэффициентам с помощью подходящего преобразования, которые могут быть записаны в общем виде следующим образом [1]:
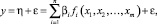 (1)
(1)
где fi(x1, x2, …, xm) – произвольные функции факторов (регрессоров); β1, β2,…, βk – коэффициенты модели; ε – ошибка эксперимента.
Исходя из закона действующих масс [16, 18] зависимость концентрации фенольного соединения от факторов процесса математически можно представить следующим выражением:
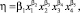 (2)
(2)
где η – уровень остаточной концентрации BPA в момент времени t, мг/л; x1 – исходная концентрация ВРА, мг/л; x2 – концентрация перекиси водорода, мг/л; x3 – концентрация хлорида железа (III), г/л; x4 – время процесса очистки, ч; β1, β2, β3, β4, β5 – параметры модели.
Коэффициенты в модель (2) входят нелинейно, но при линеаризации путем логарифмировании по натуральному основанию, правой и левой частей уравнения (2), получим
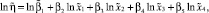
где в соответствии с (1)
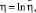
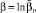
f1 = 1, 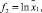
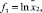
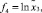
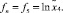
Однако при таком преобразовании случайное возмущение (ошибка эксперимента) входит в модель мультипликативно и имеет логнормальное распределение, т.е. 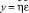 , и после логарифмирования это дает
, и после логарифмирования это дает
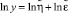 [1].
[1].
После линеаризации и введения новых переменных выражение (2) примет вид
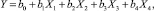 (3)
(3)
где предикторные переменные X1, X2, X3, X4 и отклик Y являются логарифмическими функциями:
Y = lny, X1 = lnx1,
X2 = lnx2, X3 = lnx3, X4 = lnx4;
b0, b1, b2, b3, b4 – параметры модели.
Обычно в задачах обработки данных матрица эксперимента и вектор отклика известны неточно, т.е. с погрешностями, и задача определения регрессионных коэффициентов по методу наименьших квадратов неустойчива к ошибкам в исходных данных [15]. При плохой обусловленности информационной матрицы FTF (F – матрица регрессоров) МНК-оценки обычно неустойчивы. Для преодоления плохой обусловленности информационной матрицы предложена идея регуляризации, обоснованная в работах А.Н. Тихонова [12–15].
Применительно к решению регрессионных задач идея регуляризации А.Н. Тихонова интерпретирована А.Э. Хоэрлом как процедура «гребневой регрессии». При использовании метода «гребневой регрессии» для стабилизации МНК-оценок (определяемых b = (FTF)–1FTY) регуляризация связана с добавлением некоего положительного числа τ (параметра регуляризации) к диагональным элементам матрицы FTF [2].
Выбор параметра регуляризации τ Хоэрл, Кеннард и Белдвин [2, 3] предложили осуществлять следующим образом:
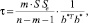 (4)
(4)
где m – количество параметров (без учета свободного члена) в исходной модели регрессии; SSe – остаточная сумма квадратов, полученная по исходной модели регрессии без корректировки на мультиколлинеарность; b* – вектор-столбец коэффициентов регрессии, преобразованный по формуле
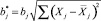 ,
,
где bj – параметр при переменной Xj в исходной модели регрессии, определенный по МНК; 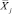 – среднее значение j-й независимой переменной.
– среднее значение j-й независимой переменной.
После выбора величины τ формула для оценки регуляризованных параметров регрессии будет иметь вид
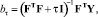 (5)
(5)
где I – единичная матрица; F – матрица регрессоров; Y – вектор значений зависимой переменной.
Величина параметра регуляризации, определяемая по формуле (4), принимает значение, равное τ = 1,371·10–4.
Регуляризованная модель снижения концентрации фенольного соединения, построенная в системе Statistica с учетом формулы (5), может быть представлена в виде
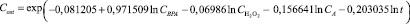 (6)
(6)
где Сост и СВРА – остаточная и начальная концентрации фенольного загрязнителя соответственно, мг/л; 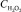 – концентрация перекиси водорода, мг/л; СА – концентрация хлорида железа (III), г/л; t – время, ч.
– концентрация перекиси водорода, мг/л; СА – концентрация хлорида железа (III), г/л; t – время, ч.
Значения коэффициента детерминации, R2 = 0,9995, критерия Фишера F = 5348,417, превышающего критическое значение (Fкр(0,01; 4,11) = 5,67), характеризуют адекватность регуляризованной модели результатам эксперимента на уровне значимости α = 0,1.
Определение оптимальных удельных значений концентраций химических реагентов (FeCl3, H2O2), необходимых для очистки воды, при достижении минимального удельного уровня затрат представляет собой задачу нелинейного (выпуклого) программирования вида (7–9) [7]:
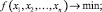 (7)
(7)
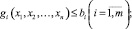 (8)
(8)
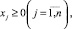 (9)
(9)
где f – функция финансовых средств, связанная с запасом химических реагентов f = Z(c2, c3); gi – функция снижения концентрации фенольного соединения в водной среде в процессе физико-химической очистки, g = Cost(с1, c2, c3, t) (функция ограничения); x1, x2,…, xn – параметры процесса; x1 – начальная концентрация фенольного соединения, х1 = c1, мг/л; х2 и х3 ‒ концентрации перекиси водорода и хлорида железа (III) соответственно х2 = c2, мг/л, х3 = с3, г/л; t – время, ч; bi – предельно допустимая концентрация фенольного соединения (ПДК), мг/л.
Функцию финансовых средств, представляющую двухноменклатурную модель затрат, связанную с запасом перекиси водорода и хлорида железа (III), с учетом формулы Вильсона можно представить в виде [10]
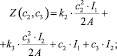 (10)
(10)
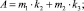
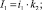
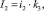
где Z(c2, c3) – удельные суммарные затраты, связанные с запасом, руб.; A – удельные накладные затраты одной общей поставки, руб.; c2 – удельное потребление перекиси водорода, мг/л; c3 – удельное потребление хлорида железа, г/л; I1, I2 – удельные тарифы затрат на хранение перекиси водорода и хлорида железа (III) соответственно, руб.; m1, m2 – доля цены продукции, приходящаяся на затраты на выполнение одного заказа по перекиси водорода и хлориду железа (III) соответственно; i1, i2 – доля цены продукции, приходящаяся на затраты на содержание запаса по перекиси водорода и хлориду железа (III) соответственно; k2, k3 – удельная закупочная цена единицы запаса перекиси водорода (руб./мг) и хлорида железа (III) (руб./г) соответственно.
Для решения системы (7)–(9) вводится набор переменных λ1, λ2, …, λm, называемых множителями Лагранжа, составляют функцию Лагранжа:
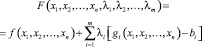 ,
,
находятся частные производные 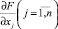 и
и 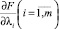 и рассматривается система n + m уравнений
и рассматривается система n + m уравнений
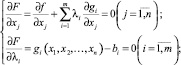 (11)
(11)
c n + m неизвестными x1, x2, ..., xn; λ1, λ2, ..., λm. Всякое решение системы уравнений (11) определяет условно-стационарную точку, в которой может иметь место экстремум функции f(x1, x2, ..., xn). При соблюдении условий Куна ‒ Таккера (12.1)–(12.6) точка 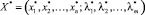 является седловой точкой функции Лагранжа, т.е. найденное решение задачи (7)–(9) оптимально [5, 7]:
является седловой точкой функции Лагранжа, т.е. найденное решение задачи (7)–(9) оптимально [5, 7]:
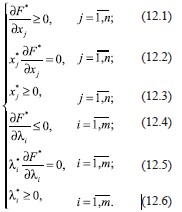
Задача идентификации оптимальных параметров процесса очистки промышленных сточных вод от фенольных соединений при достижении минимального уровня текущих удельных затрат, необходимых для обесфеноливания вод, решалась при следующих исходных данных: начальная концентрация фенольного загрязнителя в сточных водах 0,006 мг/л (6ПДК); время очистки, определенное технологическим процессом, – 5 суток (120 часов); предельно допустимая концентрация загрязнителя 0,001 мг/л (b = 0,001); удельная закупочная цена единицы запаса по перекиси водорода 24,5·10‒6 руб./мг (k2 = 24,5·10‒6), по хлориду железа (III) 37,5·10‒3 руб./г (k3 = 37,5·10‒3); доля цены продукции, приходящаяся на затраты по содержанию запаса по перекиси водорода и хлориду железа, равна соответственно 10 % (i = 0,1) и 12 % (i = 0,12); доля цены продукции, приходящаяся на затраты по выполнению заказа по перекиси водорода и хлориду железа 5 % (m1 = 0,05) и 7 % (m2 = 0,07) соответственно.
Решая задачу (7)–(9) в системе MathCad, получаем точку X* с координатами
(с2*, с3*, λ*) = (6,361∙103; 5,694; 1,346·104),
в которой соблюдаются условия Куна – Таккера (12.1)–(12.6). Существует точка, принадлежащая области допустимых решений, в которой выполняется условие регулярности Слейтера:
Сost(c2°, c3°) = Сost (103,1) = – 7,22·10–9 < 0.
Вид условно-стационарной точки определялся в соответствии с критерием Сильвестра [5] применительно к матрице Гессе функции Лагранжа:
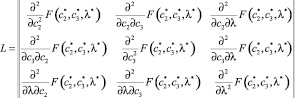
В соответствии с критерием Сильвестра матрица L является ни положительно, ни отрицательно определенной (полуопределенной) (Δ1 = 4,772·10–8 ≥ 0; Δ2 = 6,639·10–9 ≥ 0; Δ3 = ‒5,042·10–17 ≤ 0).
Из выполнения условий Куна – Таккера, регулярности Слейтера и на основе исследования знакоопределенности матрицы Гессе функции Лагранжа в условно-стационарной точке следует, что точка (6,361∙103; 5,694; 1,346·104) является седловой точкой функции Лагранжа, т.е. оптимальным решением задачи (7)–(9).
Таким образом, для снижения уровня фенолов в промышленных сточных водах с 0,006 мг/л (6 ПДК) до предельно допустимого (0,001 мг/л), потребуются удельные текущие затраты в размере 1,545 руб./л. Данное значение удельных затрат является минимальным при использовании в процессе очистки оптимальных удельных уровней расхода перекиси водорода 6,361·103 мг/л и хлорида железа (III) 5,694 г/л.
Методом множителей Лагранжа для технико-экономических условий (с1 = 0,006 мг/л; t = 120 ч; b = 10–3 мг/л; k2 = 24,5·10–6 руб./мг, k3 = 37,5·10–3 руб./г; i1 = 10 %, i2 = 12 %; m1 = 5 %, m2 = 7 %) решена задача определения оптимальных удельных значений ингредиентов, используемых в качестве окислителей в фотокаталитическом процессе разложения фенольного соединения, содержащегося в промышленных сточных водах до уровня ПДК.
Идентифицированная регуляризованная математическая модель, устанавливающая зависимость уровня снижения концентрации фенольного соединения в водной среде от параметров процесса фотохимической очистки, обладает лучшими прогнозными свойствами, чем модель, определяемая по методу наименьших квадратов. С использованием полученной регуляризованной математической модели методом множителей Лагранжа решена задача математического программирования по определению оценок оптимальных удельных уровней расхода химических реагентов (FeCl3, H2O2), являющихся устойчивыми решениями.
Рассмотренный подход к идентификации оптимальных параметров процесса фотохимической очистки с применением регуляризации позволит обеспечивать эффективное управление очисткой сточных вод от фенольных соединений.
Рецензенты:
Яшин А.А., д.т.н., д.б.н., профессор кафедры «Общая патология» Медицинского института, ФГБОУ ВПО «Тульский государственный университет», г. Тула;
Короткова А.А., д.б.н., профессор, заведующая кафедрой биоэкологии и туризма, ФГБОУ ВПО «Тульский государственный педагогический университет им. Л.Н. Толстого», г. Тула.
Работа поступила в редакцию 16.02.2015.



