Для проектирования космических аппаратов необходимо знать аэродинамические характеристики вдоль всей траектории – от орбитального полета до посадочного режима. Значение этого фактора многократно возрастает, когда он применяется для построения быстрых инженерных методов расчета на этапе предварительного проектирования. Аэродинамические характеристики космического аппарата (КА) в свободномолекулярном режиме являются предельными значениями траектории наибольшей высоты и максимальной скорости полета и могут быть вычислены точно. Аэродинамические характеристики космического аппарата определяются столкновениями молекул набегающего потока газа с поверхностью без учета межмолекулярных столкновений, и для этого используются методы свободномолекулярной газовой динамики [2, 6, 7]. Исследование течений газа в переходной области между течениями сплошной среды и свободномолекулярным представляет собой достаточно сложную задачу. Для анализа аэродинамических характеристик КА в переходном режиме, необходимо решать полное интегро-дифференциальное уравнение Больцмана для функции распределения с семью независимыми переменными [7]. Единственными методами, позволяющими преодолеть трудности решения уравнения Больцмана, являются методы Монте-Карло [2].

Решение уравнения Больцмана при малых числах Кнудсена, особенно для сложных тел – задача чрезвычайно трудоемкая. В этой связи естественным является появление и развитие инженерных методов, обоснованных совокупным материалом экспериментальных, теоретических, численных результатов, дающих возможность предсказания аэродинамических характеристик (АДХ) сложных тел в переходном режиме. Метод основан на так называемой гипотезе локальности, предполагающей, что поток импульса на элемент поверхности определяется местным углом его наклона к набегающему потоку. Обработка экспериментальных данных показывает, что точность теории локального взаимодействия вполне приемлема для инженерных расчетов аэродинамических характеристик широкого класса тел на этапе предварительного проектирования [1].

В конце девяностых – начале двухтысячных годов на факультете по инициативе профессора Ю.И. Хлопкова был разработан проект информационной технологи «АДАНАТ» – Аэродинамический Анализ обеспечения создания Авиационно-космической Техники [8]. В рамках проекта информационной технологии «АДАНАТ» разработан комплекс методов, обеспечивающих анализ и проектирование гиперзвуковых летательных аппаратов произвольной формы на важнейших участках траектории - необходимого инструмента при создании нового поколения авиационно-космической техники. Траектория воздушно-космической системы на этапах от схода с орбиты до приземления перекрывает все мыслимые режимы аэродинамического обтекания. В этой связи был разработан ряд базовых моделей, методов, алгоритмов и программ, разработанных или адаптированных на ФАЛТ и хорошо себя зарекомендовавших при расчёте аэродинамических характеристик гиперзвуковых летательных аппаратов (ГЛА).

Целью настоящей работы является создание в применении программ для исследования аэродинамических характеристик аэрокосмических летательных аппаратов в разреженной атмосфере на всех участках траектории полет – от орбитального до посадочного режима.

Методика расчета аэродинамических характеристик гиперзвуковых летательных аппаратов в переходном режиме

В настоящее время локальный метод условно можно использовать к вычислению аэродинамических характеристик воздушно-космических аппаратов на всех участках траектории полета – орбитальный полет, вход в атмосферу, торможение, аэродинамический маневр в плоскость посадочной полосы, снижение скорости до посадочной, приземление [8].

Обычно режимы полета связывают безразмерным числом Кнудсена или числом Рейнольдса. Метод состоит в построении функции аппроксимации при известных предельных значениях: свободномолекулярного С(0) и сплошносредного, обычно моделируемого по методу Ньютона С(∞).

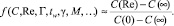
Функция f зависит от свойств газа, параметров набегающего потока, геометрии поверхности и др.

В данной работе используется классический метод локальности и предполагается

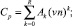
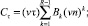
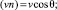
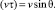
В предельном случае сплошной среды по методу Ньютона получаем

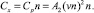
В другом предельном свободномолекулярном случае получаем

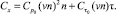
Трудности решения аэродинамических задач обтекания пространственных тел потоком разреженного газа вызвали развитие инженерных полуэмпирических методов, использующих накопленные экспериментальные и расчетные данные. Описываемый метод основан на гипотезе локальности, которая состоит в следующем: аэродинамические коэффициенты сил, действующих на элемент поверхности, зависят только от местного угла наклона q этого элемента к вектору скорости набегающего потока, от характерного для всего тела числа Rе₀ = ρ_∞V_∞D/μ₀ и температурного фактора tw = T_w/T₀, где μ0 = μ(T₀) – коэффициент вязкости, вычисляемый по температуре торможения; T0, Tw – температура торможения и стенки соответственно; D – диаметр сферы, основания конуса. Для элементарных сил давления и трения в форме работы [4]

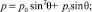
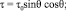
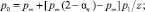
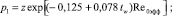
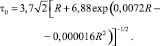
Здесь

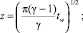
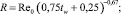
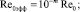
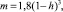
где h – относительные поперечные размеры аппарата, равный отношению его высоты к длине. Здесь коэффициенты p0, p1, t0 (коэффициенты режима течения) зависят от числа Рейнольдса Re0 = ρ_∞V_∞L/μ₀, в котором коэффициент вязкости m0 вычисляется при температуре торможения T0. Кроме числа Рейнольдса наиболее важным параметром является температурный фактор t_w = T_w/T₀, где T₀, T_w – температура торможения и температура поверхности.

В рассматриваемых методах не учитывается влияние взаимодействия пограничного слоя с гиперзвуковым невязким потоком при больших числах Rе0. Расчетные и экспериментальные значения Cх конуса в переходном режиме согласуются удовлетворительно, данные по Cy согласуются значительно хуже. Таким образом, локальный метод расчета аэродинамических характеристик тел в гиперзвуковом потоке разреженного газа в переходном режиме дает хороший результат по Cх для широкого класса тел и качественно верный результат по Cy. При малых углах атаки (a < 5°) точность результата ухудшается, в этом случае необходимо привлекать более полные модели, учитывающие наличие пограничного слоя.

Результаты исследования и их обсуждение

Представлены результаты расчета коэффициентов силы сопротивления Cx, подъемной Cy, момента тангажа mz для аэрокосмических летательных аппаратов [3, 5, 9–14] (рис. 1). Расчеты проводились с использованием локального метода в диапазоне углов атаки a от –90° до 90°. Параметры задачи были следующие: отношение теплоемкостей g = 1.4; температурный фактор tw = Tw/T0 = 0,001; число Рейнольдса Rе0 = 0, 1, 10, 100, 1000, 10000.

 а   б

Рис. 1. Геометрические представления вариантов аэрокосмических летательных аппаратов

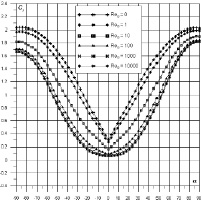 а   б

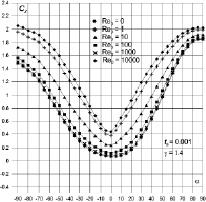
Рис. 2. Зависимость Cx(a) для воздушно-космических аппаратов а и б

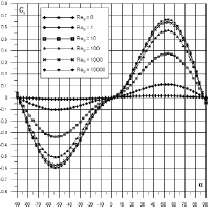 а  б

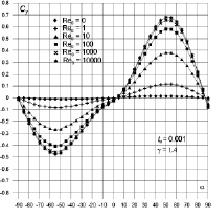
Рис. 3. Зависимость Cy(a) для воздушно-космических аппаратов а и б

На рис. 2 и 3 представлены зависимости Cx(a), Cy(a) при различных значениях числа Рейнольдса для воздушно-космических аппаратов а и б. Из этих результатов видно, что с увеличением числа Рейнольдса коэффициент сопротивления тела уменьшается (что можно объяснить уменьшением нормальных и касательных напряжений p1(Re0) и t0(Rе0)). При больших числах Рейнольдса Re0 ≥ 106 характеристики почти не изменяются.

Зависимость Cy(a) растает с увеличением числа Рейнольдса (что можно объяснить увеличением нормальных и касательных напряжений p1(Re0) и t0(Rе0)). Значения mz(a) весьма чувствительны к изменению числа Рейнольдса.

Заключение

Проведено исследование аэродинамических характеристик гиперзвуковых летательных аппаратов в потоке разреженного газа методом по гипотезе локальности с привлечением полуэмпирических теорий. Представлены результаты расчетов локальным методом аэродинамических характеристик аэрокосмических летательных аппаратов в режиме гиперзвукового течения при различных значениях числа Рейнольдса Re0. Предложенная методика хорошо зарекомендовала себя для расчета гиперзвукового обтекания выпуклых не очень тонких и пространственных тел на этапе предварительного проектирования. Таким образом, локально-инженерный метод можно использовать при исследовании аэродинамических характеристик гиперзвуковых летательных аппаратов в переходном режиме.

Работа выполнена при поддержке Российского Научного Фонда (РНФ проект № 14-11-00709).

Рецензенты:

Боголепов В.В., д.ф.-м.н., профессор, ФГУП ЦАГИ, г. Жуковский;

Липатов И.И., д.ф.-м.н., профессор, начальник отдела, ФГУП ЦАГИ, г. Жуковский.

Работа поступила в редакцию 16.02.2015.