Актуальной проблемой в современном производстве минераловатной продукции является учет расхода расплава. Традиционные методы измерения расхода жидкости в данной ситуации не применимы из-за агрессивности среды. Определение расхода расплава по изменению тока двигателя валков центрифуги, по количеству загруженного сырья, по весу готовой продукции являются недостаточно эффективными для предъявляемых на сегодняшний день требований к планированию производственных затрат. Между тем постоянный контроль расхода расплава c целью мониторинга работы центрифуги и обеспечения заданных параметров минераловатного ковра является одной из самых важных задач производства.
В настоящее время наиболее перспективными устройствами оценки дебита расплава считаются приборы на основе систем технического зрения [3, 5–7]. Такие приборы позволяют бесконтактным способом оценивать параметры струи (скорость истечения, диаметр), необходимые для расчета мгновенного значения ее дебита. Заметим, что в реальном производстве диаметр струи и скорость ее истечения оказываются нестабильными. Поэтому для проверки работоспособности алгоритма оценки параметров струи расплава требуется большое количество экспериментальных данных. В связи с тем, что отработать алгоритм в реальных условиях (на производстве) не представляется возможным, необходимо компьютерное моделирование процесса истечения нагретой струи в холодное пространство. Создание и визуализация математической модели позволяет гибко задавать необходимые начальные условия, изменять параметры истечения струи расплава и тем самым провести эксперименты без лишних производственных затрат. Кроме того, 3D модель обеспечивает наглядность эксперимента.
Основная часть
Теоретическое изучение процесса истечения расплава показало, что характер истечения расплава зависит от многих факторов, и является функцией f(g, u, ρ, σ, η, H, d, h), где g – ускорение свободного падения, u – скорость истечения, ρ – плотность расплава, σ – поверхностное натяжение жидкости, η – кинематический коэффициент вязкости, H – высота напора, d – диаметр стока, h – высота падения струи. Кроме этого, струя имеет температуру, отличающуюся от окружающегося воздуха. Решение задачи теплообмена между покоящимся воздухом и нагретой струей возможно лишь после того, как будут определены законы изменения температуры вдоль струи и в её поперечном сечении [7].
Для полной постановки задачи необходимо определить режимные и конструктивные характеристики конкретного производственного процесса. Расплав из плавильного агрегата попадает в прямоугольный фидер, который несет функцию гомогенизатора. Лётка имеет прямоугольную форму размером 60×100 мм. Будем считать d = 100 мм. За счёт значительного температурного перепада на выходе струи происходит образование корки, которая уменьшает площадь сечения отверстия и изменяет его до овальной формы. Величина напора H в плавильном агрегате с боковым вариантом выдачи расплава обычно мала по отношению к размерам отверстия H ≈ 25...65 мм, следовательно, отверстие считается большим, и при расчете истечения расплава необходимо учитывать напоры, действующие по его кромкам. Толщина стенки плавильного агрегата l = 380 мм, что превышает три размера отверстия (3d), следовательно, стенка считается толстой и характер истечения аналогичен характеру истечения через насадку.
Насадками называются короткие трубки, монтируемые, как правило, с внешней стороны резервуара таким образом, чтобы внутренний канал насадки полностью соответствовал размеру отверстия в стенке. Наличие такой направляющей трубки приводит к увеличению расхода расплава при прочих равных условиях. В [1] авторы отмечают причины увеличения расхода. При отрыве струи от кромки отверстия струя попадает в канал насадки, а поскольку струя испытывает сжатие, то стенок насадки она касается на расстоянии от 1,0 до 1,5 его размера d. Воздух, который первоначально находится в передней части насадки, вследствие неполного заполнения его жидкостью постепенно выносится вместе с потоком жидкости. Таким образом, в этой области образуется «мёртвая зона», давление в которой ниже, чем давление в окружающей среде. При истечении в атмосферу в «мёртвой зоне» образуется вакуум. За счёт этих факторов увеличивается перепад давления между резервуаром и областью за внешней его стенкой и в насадке генерируется так называемый эффект «подсасывания» расплава из резервуара. Однако наличие насадка увеличивает гидравлическое сопротивление для струи жидкости, т.к. в насадке появляются потери напора по длине, но влияние подсасывающего эффекта компенсирует дополнительные потери напора по длине. На практике эти эффекты (подсасывание и дополнительные сопротивления по длине) компенсируются при соотношении: l = 5,5d. В нашем случае l = 380 мм, следовательно, l < 5,5d. Таким образом, подсасывающий эффект приводит к увеличению расхода Q.
Вся потенциальная энергия жидкости в фидере расходуется на кинетическую энергию струи, вытекающей в газообразную среду, находящуюся под атмосферным давлением. Коэффициент истечения зависит от числа Рейнольдса, которое определим по формуле
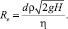
Подставим значения d = 60 мм, h = 20–45 пз, r = 2500 кг/м3, g = 9,81 м/с Н = 50 мм получим Re = 3–7. Малое значение числа Рейнольдса указывает на ламинарный характер истечения жидкости [2]. Однако при моделировании процесса было установлено, что после истечения из отверстия (стока) расплав движется струйно, затем в зависимости от неоднородности вещества расплава и температурных изменений происходит деформация струи (рис. 1, а). Во многих случаях струя начинает изгибаться, образовывать складки или принимать скрученную форму (рис. 1, б).
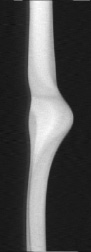 а
а 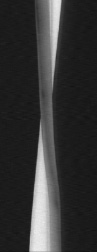 б
б
Рис. 1. Формы деформации струи расплава: а – неоднородность; б – скручивание
Струю расплава можно разделить на три участка: начальный, переходный и основной [1]. В начальном участке изменения температур, плотностей, массы происходят в пограничном слое струи. Он заканчивается, когда пограничный слой распространяется по поперечному сечению струи. Движение жидкости в начальном и переходном участках осуществляется под действием положительного градиента давления, поэтому эти два участка можно рассматривать как единый участок. Кроме того, переходный участок имеет незначительную протяжённость, по сравнению с основным участком. Для рассматриваемого алгоритма оценки параметров струи представляет интерес основной участок или участок свободного падения.
Визуализация движения струи расплава является задачей трёхмерного моделирования. При реализации модели необходимо учесть следующие особенности, характеризующие производство минераловатного ковра:
■ на изображении струи расплава должны появляться пятна, соответствующие температурным изменениям расплава и различной вязкости вещества;
■ механические воздействия определяют отклонение свободного падения струи и изменение её формы;
■ появление сгустков в струе вызывает изменение геометрии струи.
Для реализации модели необходимо выполнить следующие подзадачи: визуализация вязкой жидкости, моделирование движения жидкости, моделирование изгибов и скрутки струи.
Моделирование жидкости связано с решением нелинейных дифференциальных уравнений, которые в общем случае не имеют аналитического решения. Для того чтобы найти решение, обычно, используются численные методы. Представляет интерес метод моделирования вязкой жидкости, называемый SPH (Smoothed Particle Hydrodynamics) – гидродинамика сглаженных частиц [4]. В отличие от основанных на сетке методик, которые прослеживают границы жидкости, метод SPH создаёт свободную поверхность для непосредственно взаимодействующих жидкостей или газов. SPH представляет собой численный метод, который позволяет проводить расчеты течений с сильными деформациями границ расчетной области, которые допускают изменение связности области расчета. Согласно методу SPH для каждой частицы жидкости вычисляется пространственный хэш (индекс), далее все хэши собираются в таблицу и сортируются так, чтобы частицы с одинаковыми хэшами были рядом. Параллельно создается специальная таблица, которая позволяет быстро найти всех соседей конкретной частицы, то есть по значению хэша получить все остальные частицы с таким же хэшем.
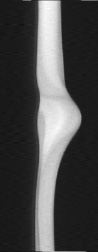 а
а  б
б
Рис. 2. Визуализация жидкости: а – снимок; б – модель
 а
а  б
б
Рис. 3. Скручивание жидкости: а – снимок; б – каркас модели
В связи с тем, что частицы рассчитываются и визуализируются отдельно друг от друга, жидкость не выглядит однородной, она как бы состоит из отдельных элементов (частиц). Так как для визуализации рассматриваемой модели более важным является внешняя форма анализируемого объекта, чем внутренняя, то и задачу визуализации можно упростить, моделируя только внешние стенки жидкости. При этом формы изгибов и скручивание струи реализуются с помощью сплайнов, создавая каркас модели (рис. 2 и 3), а сама жидкость с помощью метода SPH. Моделируемая жидкость «течет» по рассчитанному каркасу.
Все вычисления визуализации струи можно представить в виде конвейерной архитектуры (рис. 4) [4].

Рис. 4. Алгоритм моделирования вязкой жидкости
В блоке «Расчет сетки каркаса» вычисляются внешние стенки струи, операции вращения и сдвига выполняются умножением на соответствующие матрицы аффинных преобразований, волны моделируются с помощью кривых Безье.
Рис. 5. Моделирование сложной формы струи
В блоке «Массив частиц» выполняется заполнение массива частиц по поперечному сечению решетки с расстояниями между частицами 3r, где r – радиус частицы.
В блоке «Расчет сил» вычисляются силы, возникающие вследствие взаимодействия частиц друг с другом, c учетом силы притяжения к каркасу струи.
В блоке «Расчет диффузии» значения яркости температуры от частицы передается ее соседям в соответствии с законом диффузии.
Блок «Рендеринг» необходим для визуализации нескольких тысяч одинаковых частиц. Частицы рисуются в два специальных буфера: буфер цвета и буфер высот. Первый используется для придания жидкости необходимого цвета, а второй – для вычисления скоростей и нормалей, необходимых для бликов и преломлений.
Задача визуального моделирования движения жидкости выполнена с помощью графического стандарта OpenGL. Графическая библиотека позволяет создавать сложные трёхмерные сцены из простых примитивов (рис. 5).
Она используется при создании компьютерных игр, виртуальной реальности, визуализации в научных исследованиях.
Заключение
Входными данными для математической модели являются: температура расплава, геометрические размеры лётки, величина напора, коэффициент кинематической вязкости, плотность расплава и периодичность механических воздействий на струю расплава. Выходными – скорость движения струи, площадь поперечного сечения струи и рассчитанный дебит расплава.
В компьютерной модели форму струи жидкости определяет форма летки. Изначально форма отверстия считается овальной, поэтому струя имеет в сечении форму круга. Затем при нарастании корки отверстие приобретает форму треугольника, при этом струя изменяет форму. Изменять величину напора можно с помощью параметра H. При этом изменяется скорость движения частиц в струе и происходит отклонение струи по горизонтали.
Программа моделирования струи позволяет просматривать процесс истечения из любой точки пространства.
Рецензенты:
Доросинский Л.Г., д.т.н., профессор, заведующий кафедрой «Теоретические основы радиотехники», Уральский федеральный университет, г. Екатеринбург;
Поршнев С.В., д.т.н., профессор, заведующий кафедрой «Радиоэлектроника информационных систем», Уральский федеральный университет, г. Екатеринбург.
Работа поступила в редакцию 02.03.2015.



