Одной из важных задач теории механизмов и машин является задача синтеза их структур. За более чем полуторавековую историю науки о машинах, если её отсчитывать от основополагающих научных статей академика Чебышева П.Л. (1852–1870 гг.), когда в частности им был обоснован метод структурного анализа плоских шарнирных механизмов [4] с использованием формулы
3n – 2p = 1, (1)
в которой через n обозначалось число подвижных звеньев кинематической цепи, через р – число одноподвижных кинематических пар – шарниров, а единица определяла общую подвижность механизма. Были разработаны три метода структурного синтеза кинематических цепей – это метод [5] немецкого ученого Грюблера М.Ф. (1873 г.), метод [1] российского ученого Ассура Л.В. (1913 г.) и метод [2] одного из авторов настоящей статьи (1993 г.). Несмотря на то, что метод Грюблера был разработан более 140 лет назад, он (метод) не потерял своей актуальности до настоящего времени благодаря его очевидной практической применимости.
Общий подход Грюблера при создании замкнутых цепей
Чтобы воспользоваться методом Грюблера, достаточно особым образом построить такие кинематические цепи, при остановке в которых отдельных звеньев цепи получать вполне работоспособные механизмы. Цепи, предложенные Грюблером, впоследствии получили название «цепей Грюблера». Сам Грюблер в работе [5] показал лишь общий подход к отысканию таких цепей с использованием системы уравнений
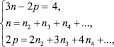 (2)
(2)
где n2, n3, n4 – соответственно числа двух-, трех-, четырех- и т.д. парных звеньев.
Первое уравнение системы (2) было заимствовано из работы [4] Чебышева П.Л. и преобразовано Грюблером к свободным замкнутым цепям, обладающим тремя независимыми движениями в плоскости и одной внутренней относительной подвижностью звеньев.
Используя систему (2), Грюблер показал, что цепи, которые ей удовлетворяют, могут иметь лишь четное число звеньев n = (4 + 2p)/3. Обратим внимание на то, что это равенство имеет одно особое решение, когда р принимает значение, равное единице. В этом случае n оказывается равным двум (n = 2). Эта цепь становится соответствующей условию Грюблера. Все другие нечетные числа р от трех и выше не дают целого значения n.
Трудно предположить, по какой причине сам автор метода (Грюблер) не рассмотрел структуры цепей ни с n = 2, ни даже с n = 4 и n = 6, в то время как цепям с n = 8 посвятил достаточно большое внимание. Он построил двенадцать таких цепей и тем самым методически позволил его последователям найти более простые, а именно четырех- и шестизвенные цепи.
Все эти цепи приведены нами на рис. 1, а именно, двухзвенная (а), четырехзвенная (b) и две отличающиеся друг от друга шестизвенные цепи (с1 и с2).
Казалось бы, что цепь (а) (впервые приводимая в настоящей работе) не вполне удовлетворяет условиям Грюблера, а именно условию замкнутости. Однако она именно замкнутая, т.к. не имеет открытых шарниров, к которым можно было бы присоединить другие звенья. Эта цепь не просто увеличивает общее число цепей Грюблера, она обладает особым качеством, т.к. может быть использована как исходная – «материнская» цепь для построения всех других – более сложных.
Универсальный метод создания структур цепей Грюблера
Покажем, как можно организовать четырехзвенную цепь (рис. 1, b) из исходной двухзвенной цепи.
Если к двухзвенной цепи с шарниром А (рис. 1, а) прибавить на открытых концах звеньев 1 и 2 два шарнира В и С, то появится структура, удовлетворяющая условию W = 0 (n = 2, p = 3), т.е. группа нулевой подвижности – группа Ассура. Если далее к любому открытому шарниру А или В добавить одно звено 3 с шарниром D, то цепь станет механизмом, т.е. её подвижность окажется равной W = 1 (n = 3, p = 4). Далее, если шарниры D и С замкнуть ещё одним звеном 4 без добавления шарниров, то получим новую цепь Грюблера с подвижностью W = 4 (n = 4, p = 4). Этот алгоритм может быть использован для получения и шестизвенных цепей, путем добавления к четырехзвенной цепи двух шарниров, звена с шарниром, затем звена без шарнира. Причем произвести эти добавления можно разным способом – или добавляя шарниры к рядом находящимся звеньям 2 и 3, что дает цепь с двумя замкнутыми четырехугольными контурами (рис. 1, c1), или добавляя шарниры к противоположно находящимся звеньям 2 и 4, что дает иную шестизвенную цепь с одним четырехугольным и одним пятиугольным замкнутыми контурами (рис. 1, c2). Цепи эти отличаются и тем, что по внешнему обходу в цепи в1 шесть звеньев, а в цепи в2 – пять звеньев.
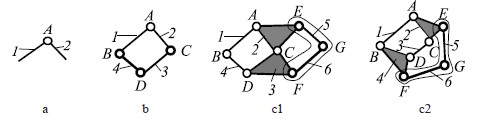
Рис. 1. Простейшие цепи Грюблера
Обе эти цепи удовлетворяют условиям Грюблера, а именно в них по шесть звеньев и по семь шарниров, т.е. их подвижность по (2) W = 4, к тому же в них по два трехпарных (n3 = 2) и по четыре двухпарных звеньев (n2 = 4) и n2 + n3 = 6, т.е. удовлетворяется условие р = 7 и 2p = 2n2 + 3n3.
Практическую значимость метода Грюблера можно показать, изобразив описанные двух-, четырех- и шестизвенные цепи в виде механизмов, появляющихся при остановке одного из звеньев цепи (рис. 2). Останавливая звено 1 (схема а), получаем однозвенный приводной механизм, останавливая любое из четырех звеньев цепи (схема b), получаем шарнирный четырехзвенник. Последовательно останавливая поводки 1 или 4, или 5, или 6 шестизвенной цепи (с1), можно построить механизмы (с) и (d), отличающиеся лишь ведущим звеном, в схеме (с) – двухшарнирным звеном, в схеме (d) трехшарнирным.
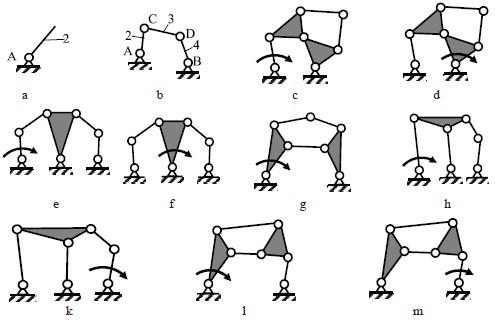
Рис. 2. Схемы механизмов, полученные из простейших двух-, четырех- и шестизвенных цепей Грюблера
При остановке звена 2 или 3 цепи (с1) (рис. 1) получим схемы механизмов (е) и (f), также отличающиеся ведущим двухшарнирным и трехшарнирным звеньями. При остановке звена 1 цепи (с2) получаем единственный механизм (g), при остановке звена 4 цепи (с2) появляются два механизма (h) и (k), отличающиеся ведущим звеном 1 или 6, а при остановке звена 5 или 6 также появятся два механизма (l) и (m), в одном из них ведущее звено трехпарное, в другом – двухпарное.
Все приведенные на рис. 2 схемы механизмов являются полным составом одно-, четырех- и шестизвенных плоских шарнирных механизмов, широко используемых в практике, т.е. относящихся к классическим. Их схемы можно видоизменять, лишь заменяя некоторые из шарниров на поступательные кинематические пары, но и этот прием вполне ограничен по числу возможных схем.
Обратимся теперь к поиску всех восьмизвенных цепей Грюблера. Выше было отмечено, что к построению таких цепей впервые обратился сам Грюблер еще в 1873 г., им было построены и приведены в работе [5] двенадцать схем, которые были предварительно описаны таблицей, показанной нами.
Эти цепи приведены нами на рис. 3 в том порядке, в котором нашел их Грюблер, и без каких-либо изменений в начертании. Отметим, что никаких пояснений к построению цепей Грюблер не оставил.
Позже к этому вопросу обращались и другие исследователи. Общий анализ таких цепей был проведен Э.Е. Пейсахом в работе [3]. Он нашел и показал всего шестнадцать цепей. На рис. 4 приводятся дополнительные к схемам Грюблера (рис. 3) пять цепей, приведенных Э.Е. Пейсахом. Отметим, что цепь № 4 Грюблера, у Пейсаха в работе [3] показана не была.
Чтобы завершить эти поиски, воспользуемся методом, который показан нами выше с использованием «материнской» цепи. Начнем нахождение восьмизвенных цепей с шестизвенной цепи (с1) (рис. 1). В этом случае при последовательном добавлении к двум разным звеньям от первого до шестого по две кинематические пары, затем звена с шарниром и звена без шарнира удалось получить семь различных структур цепей, однако шесть из них уже ранее были приведены в работах Грюблера [5] и Пейсаха [3], а цепь, показанная на рис. 5, а, в этой работе приведена впервые.
Таблица М. Грюблера, используемая при построении цепей [5]
|
Варианты |
Число двухшарнирных звеньев, n2 |
Число трехшарнирных звеньев, n3 |
Число четырехшарнирных звеньев, n4 |
|
α |
4 |
4 |
0 |
|
β |
5 |
2 |
1 |
|
γ |
6 |
0 |
2 |
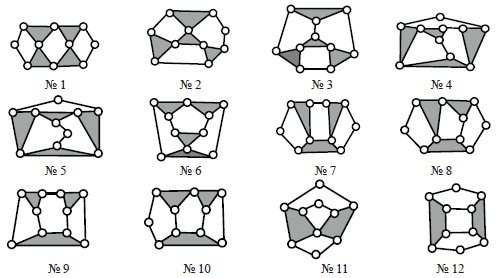
Рис. 3. Восьмизвенные замкнутые цепи, построенные Грюблером [5]
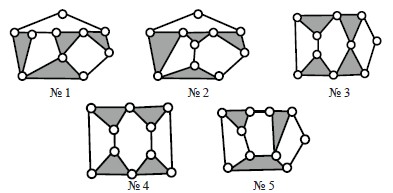
Рис. 4. Дополнительные восьмизвенные замкнутые цепи, найденные Э.Е. Пейсахом [3]
Она получена при добавлении по одному шарниру к третьему и шестому звену шестизвенной цепи (с1). При этом звено 3 из трехшарнирного становится четырехшарнирным, а двухшарнирное звено 6 – трехшарнирным. Далее присоединением звена с шарниром к одному из добавленных и введением в цепь звена без шарнира, получаем новую восьмизвенную цепь Грюблера (рис. 5, а). Используя процедуру добавления двух кинематических пар, звена с парой и звена без пары ко второй шестизвенной цепи (с2) (рис. 1), стало возможным дополнительно получить две восьмизвенные цепи, которые не были обнаружены в исследованиях [3, 5]. Первая цепь (рис. 5, b) образуется при добавлении двух шарниров к трехпарным звеньям 2 и 4, а вторая (рис. 5, с) – к трехпарному звену 2 и двухпарному звену 3. Дальнейшие процедуры, аналогичны выше описанным. Принятый порядок образования более сложных цепей Грюблера может быть обобщен в виде алгоритма, приведенного на рис. 6, где символами гА и цГ обозначены группы Ассура и цепи Грюблера с соответствующим числом звеньев в них.
Процедура построения восьмизвенных цепей Грюблера, соответствующая первому столбцу алгоритма, предусматривает последовательное добавление к «материнской» цепи трех двухзвенных групп Ассура. По второму столбцу алгоритма, создание цепей Грюблера происходит путем присоединения к «материнской» цепи четырехзвенных групп Ассура, а по третьему столбцу непосредственно к «материнской» цепи добавляются шестизвенные. По мере увеличения числа звеньев цепи алгоритм может развиваться по числу строк и столбцов. Такой подход к построению цепей Грюблера дает возможность алгоритмично, без пропусков находить все их многообразие.
С использованием описанного алгоритма, последовательно добавляя к материнской цепи (рис. 1, а), по две группы нулевой подвижности (первый столбец алгоритма), получены три новые замкнутые свободные кинематические цепи (ЗСКЦ) Грюблера (рис. 5, a, b, c); присоединением к «материнской» цепи четырехзвенных групп Ассура, а их всего две, (второй столбец алгоритма), были найдены цепи, структуры которых приведены в ранее опубликованных работах [3, 5], а при добавлении к «материнской» цепи (третий столбец), шестизвенных групп нулевой подвижности (таких групп всего десять), были построены дополнительно к уже известным в [3, 5] еще две структуры цепей. Эти цепи показаны на рис. 5, под номерами 5, d, и 5, e. Покажем на рис. 7 полный состав восьмизвенных цепей Грюблера, с включением всех структур найденных ранее М. Грюблером и Э.Е. Пейсахом.
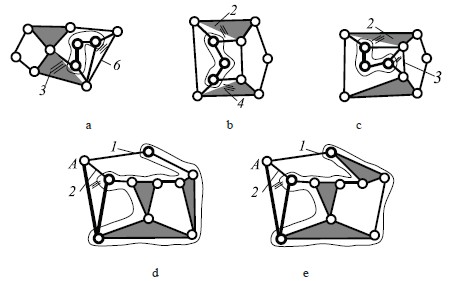
Рис. 5. Восьмизвенные цепи, полученные универсальным методом синтеза
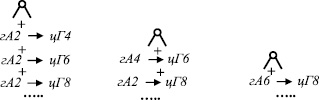
Рис. 6. Алгоритм процедур построения цепей Грюблера
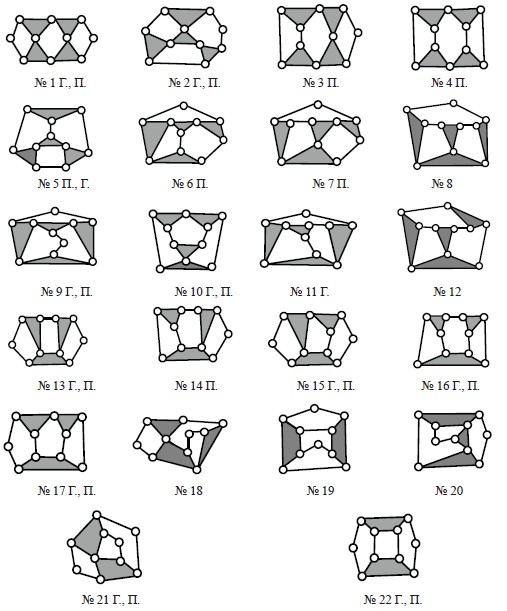
Рис. 7. Полный состав восьмизвенных цепей Грюблера
Для идентификации приведенного состава цепей (рис. 7), укажем первые буквы фамилий М. Грюблера и Э.Е. Пейсаха рядом с порядковыми номерами тех структур, которые были найдены этими учеными. Разработанный в настоящей статье метод синтеза структур ЗСКЦ Грюблера позволяет использовать его и при поиске всего многообразия более сложных – десяти-, двенадцати- и т.д. цепей с привлечением специальной поисковой компьютерной программы.
Заключение
Предложенный в настоящей статье универсальный метод поиска многообразия цепей Грюблера позволил найти дополнительно к известным семнадцати восьмизвенным цепям Грюблера пять новых структур, т.е. обосновать полный их состав в количестве 22 структур и показать применимость метода с целью отыскания более сложных по числу звеньев цепей Грюблера.
Рецензенты:
Живаго Э.Я., д.т.н., профессор, зав. кафедрой «Теоретическая механика», ФГБОУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк;
Степанов А.В., д.т.н., доцент, профессор кафедры автоматизации управления Новокузнецкого института, ФГБОУ ВПО «Кемеровский государственный университет», г. Новокузнецк.
Работа поступила в редакцию 24.02.2015



