Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

По российскому законодательству [1] «...безопасность дорожного движения – состояние данного процесса, отражающее степень защищенности его участников от дорожно-транспортных происшествий и их последствий...». Дорожно-транспортным происшествием называют [1] «...событие, возникшее в процессе движения по дороге транспортного средства и с его участием, при котором погибли или ранены люди, повреждены транспортные средства, сооружения, грузы, либо причинен иной материальный ущерб...». То есть исключаются, например, происшествия с участием только пешеходов.

Целью настоящего исследования является моделирование состояния безопасности дорожного движения.

На начальном этапе (табл. 1) исследований было проведено анкетирование студентов старших курсов факультета автомобильного транспорта – всего 30 участников. Большинство участников опроса в качестве функции отклика – показателя, определяющего безопасность движения – назвали дорожно-транспортный травматизм. Он и явился целевой функцией (отклика) в нашем исследовании.

На рис. 1 показано частотное распределение факторов – объясняющих переменных. При построении частотной выборки применялся так называемый, «трехпроцентный барьер». В итоге были отобраны 5 факторов, в наибольшей степени, по мнению респондентов, влияющие на динамику травматизма в результате ДТП:

Ф1 – среднесуточная интенсивность движения транспортных средств по магистрали (авто./сут);

Ф2 – интенсивность движения пешеходов на магистрали в час пик (чел./ч);

ФЗ – общее количество дорожно-транспортных происшествий на магистрали;

Ф4 – количество ДТП на магистрали с участием пешеходов;

Ф5 – количество нарушений на перекрестке, совершенных пешеходами.

Таблица 1

Методы исследования

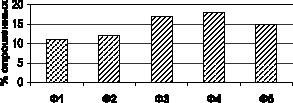
Рис. 1. Предварительный перечень факторов по результатам анкетирования

После устранения разночтений в формулировках объясняющих переменных перечень был предложен участникам анкетирования в качестве основы для ранжирования – с целью предварительной оценки степени влияния факторов на функцию отклика. Ранжирование проведено методом ранговой корреляции [2, 3]. Общий вид таблицы экспертных оценок представлен в табл. 2.

Таблица 2

Экспертные оценки

Приведем условные обозначения в расчетных формулах:

n – количество рассматриваемых факторов;

m – количество экспертов;

j – порядковый номер рассматриваемого фактора, j ∈ [1; n];

xij – ранг j-го фактора, присвоенный
i-м экспертом.

По значениям в строке «Сумма рангов» (1) рассчитали фактические ранги факторов по совокупному мнению экспертов – наибольшая значимость установлена для факторов, определяемых нарушениями правил дорожного движения, совершенными пешеходами.

Полученные значения являются приближенными и поэтому требуют оценки достоверности, которая выполняется в два этапа:

– рассчитываем коэффициент согласования (5) мнений экспертов (коэффициент конкордации Кэндалла), показывающий степень доверия к результатам ранжирования факторов;

– проверяем гипотезу о достаточной согласованности мнений экспертов, для чего расчетное значение критерия χ2 сравниваем с табличным при заданной доверительной вероятности α и числе степеней свободы n –1.

В результате обработки экспертных оценок (табл. 1) получено следующее заключение:

– по степени значимости рассматриваемые факторы расположены в последовательности: Ф4, Ф3, Ф5, Ф2, Ф1;

– коэффициент конкордации Кэндалла

– оценка экспертов является достаточной с вероятностью не ниже 0,95, поскольку

С учетом статистической достаточности выводов, сделанных экспертами в отношении значимости выбранных факторов, проведены экспериментальные исследования. Исследование охватывает временной период с января 2010 г. по июнь 2014 г. Данные по факторам Ф1...Ф4 за весь период получены в результате анализа официальных документов ОГАИ ГИБДД по Тракторозаводскому району г. Волгограда. Экспериментальные данные в отношении фактора Ф5 за период с февраля 2014 г. по июнь 2014 г. получены в результате прямых непосредственных наблюдений за дорожной ситуацией на определенном перекрестке. Наблюдения выполнялись двумя независимыми исследователями в течение 5 месяцев по 14...18 дней ежемесячно по 2...6 часов в сутки. Для повышения объективности календарные дни и время суток, в которые проводились наблюдения, менялись произвольно. Результаты наблюдения за каждый месяц усреднялись. Достоверность средних значений за период прямых непосредственных наблюдений, определенная по критерию Стьюдента, составила не менее 98 % с учетом объемов статистических выборок не менее 35 наблюдений.

Таблица 3

Усредненные результаты экспериментов

Усредненные значения, полученные в результате статистической обработки данных прямых непосредственных наблюдений, несущественно отличаются от сведений, приведенных в официальной документации за тот же временной период. Это позволило нам использовать официальные данные (фактор Ф5) за период с февраля 2014 г. по январь 2014 г. в качестве исходных данных для построения регрессионных моделей. Общий массив (табл. 3) исходных данных включает усредненные результаты 54 экспериментов, что образует выборку, репрезентативность которой достаточна для построения линейной [2, 3, 4] пятифакторной (54 > 25 = 32) регрессионной модели.

Для уточнения списка объясняющих переменных определим (1, 2) коэффициенты корреляции (табл. 4):

коэффициент корреляции «фактор – функция»

(1)

коэффициент интеркорреляции факторов

(2)

Поскольку коэффициенты интеркорреляции (2) факторов достаточно малы (< 0,7), можно говорить о слабом взаимном влиянии и, следовательно, о взаимной независимости объясняющих переменных, что позволяет включить все факторы в регрессионную модель. Вместе с тем малые значения (табл. 3) коэффициентов корреляции «фактор – функция» (1) для факторов Ф1 и Ф2 практически означают отсутствие линейной зависимости функции отклика от этих факторов, поэтому при построении модели мы рассматриваем факторы Ф3, Ф4, Ф5.

Таблица 4

Корреляция и интеркорреляция

Ранее [4, 5] мы обсуждали вопросы, связанные с корректностью построения и возможностью математического анализа регрессионных моделей, в частности, с так называемыми условиями Гаусса – Маркова. Для обеспечения выполнения комплекса условий в отношении ортогональности и ротатабельности исходных данных, выполним их нормирование [3, 4]. Фрагмент массива нормированных исходных данных и результаты моделирования приведены в следующей таблице (табл. 5).

Таблица 5

Результаты моделирования (нормированные величины)

Из представленных (рис. 2) графиков видно, что поведение прогнозной линии идентично экспериментальным данным, следовательно, модель соответствует реальному процессу.

Проверка адекватности модели по критерию Фишера при α = 0,9

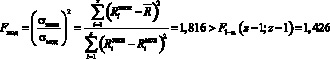
показала, что модель достаточно полно отражает закономерности моделируемого процесса.

На основании проведенного нами регрессионного моделирования можно сделать следующие выводы:

1) линейная полиномиальная модель адекватно описывает моделируемый процесс безопасности дорожного движения в г. Волгограде;

2) проведенный авторами предварительный опрос экспертов о наиболее значимых факторах, влияющих на безопасность движения, вполне согласуется с ранжированием факторов, представленных в модели;

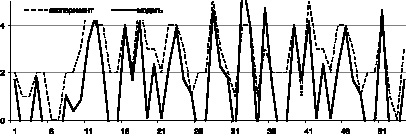
Рис. 2. Сравнение экспериментальных данных и результатов моделирования

3) руководству ГИБДД необходимо уделить особое внимание поведению пешеходов на автомагистрали и провести мероприятия, способствующие снижению общего количества дорожно-транспортных происшествий.

Мартынов В.В., д.т.н., профессор кафед­ры «Проектирование технических и технологических комплексов», ФГБОУ ВПО «Саратовский государственный технический университет им. Гагарина Ю.А.»,
г. Саратов;

Рогачев A.Ф., д.э.н., профессор, зав. кафедрой «Математическое моделирование и информатика», ФГБОУ ВПО «Волгоградский государственный аграрный университет», г. Волгоград.

Работа поступила в редакцию 26.12.2014.