Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Первое правило Чаргаффа устанавливает равенство в молекуле ДНК количества тимина (Т) и количества аденина (A), а также соответствующее равенство для гуанина (G) и цитозина (C). Позже было установлено, что аналогичное правило выполняется и для одного стренда ДНК; данное равенство было названо вторым правилом Чаргаффа. Нарушение второго правила Чаргаффа зависит от длины анализируемого участка генома и может характеризовать сам геном. Для целой хромосомы высших эукариот характерная ошибка в (приблизительных) равенствах A ≈ T, G ≈ C составляет 10–3...10–2. Правила Чаргаффа – это универсальные правила, и им подчинены геномы всех организмов от низших растений до высших животных, не являются исключением в том числе и внеклеточные формы жизни.

В настоящее время исследованию нарушения второго правила Чаргаффа посвящено не так много работ [1–4], несмотря на фундаментальный характер этого факта. Основная цель настоящей работы – оценка степени нарушения второго правила Чаргаффа в геномах различных организмов.

Материалы и методы исследования

В настоящей работе производилось исследование поведения невязки для геномов различных организмов. Геномы организмов представляли собой расшифрованные тексты нуклеотидных последовательностей, которые были взяты из EMBL банка данных. В работе использовались геномы различных организмов и вирусов; проанализированы следующие последовательности геномов: дрожжи 81 061 875 нуклеотидов, грибы 269 875 059 нуклеотидов, бактерии 36 358 967, митохондрии 243 981, вирусы 29142, а также такие организмы, как Giberella moniliformis 41 104 290, комар 230 466 657, бык 2 629 841 282, 21 хромосома человека 33 216 610, 1 хромосома макаки 232 296 185, Arabidopsis taliana 93 654 490,
дрозофилы 125 566 102, шимпанзе 106 544 938
и гориллы 9 140.

Для определения невязки составлялись частотные словари последовательностей. Частотный словарь – это множество всех символьных подпоследовательностей заданной длины, встречающихся в изучаемой последовательности, вместе с указанием частоты их встречаемости [5–7]. В рамках настоящей работы составлялись частотные словари толщины от 1 до 8 (т.е. содержащие слова длины 1, 2, …, 8).

Показателем, характеризующим степень нарушения второго правила Чаргаффа, была величина

(1)

где q – длина слов в рассматриваемом словаре; Ω – множество всех слов, являющихся прямыми; ω – слово;  – комплементарное слово; fω – частота прямого слова;  – частота комплементарного слова.

Для анализа поведения величины невязки (1) оценим её поведение для случайной нескоррелированной последовательности. Предположим, что в ней точно выполняется второе правило Чаргаффа:

p(A) = p(T); p(C) = p(G). (2)

Тогда ∀q невязка (1) равна нулю и второе правило выполняется с абсолютной точностью.

Пусть теперь соотношение (2) выполняется не точно, а с некоторой погрешностью:

p(A) = pW + ε; p(T) = pW – ε;

p(C) = pS + δ; p(G) = pS – δ. (3)

Здесь 2pW = p(A) + p(T) и 2pS = p(C) + p(G). Тогда невязка для словаря толщины q = 1 определяется выражением μ = 2(ε + δ). Для частотных словарей при q = 2 имеем три комбинации типов нуклеотидов для всех мыслимых слов: WW ⇔ WW, SS ⇔ SS и SW ⇔ SW; здесь буквы обозначают слабые и сильные нуклеотиды (т.е. W = {A, T} и S = {C, G}), а порядок не важен. Для случаев WW ⇔ WW и SS ⇔ SS возможны по три случая невязки (1) с каждой стороны палиндрома (т.е. для каждого из слагаемых
в скобках в (1):

и  (4)

и аналогично

и   (5)

Отбрасывая члены порядка ε2, δ2 и выше, получаем оценку для каждого палиндрома вида

Поскольку общее число палиндромов в частотном словаре составляет 0,5×4q, постольку окончательное выражение для оценки величины невязки (1) определяется выражением

(6)

где q – толщина словаря.

Результаты исследования
и их обсуждение

В таблице представлены результаты вычислений показателей нарушения второго правила Чаргаффа для различных организмов. Видно, что наибольшее количество нарушений второго правила Чаргаффа наблюдается для митохондрий Equus caballus breed Appalosa, далее по степени нарушения второго правила Чаргаффа следуют митохондрии парнокопытных, что еще раз свидетельствуют о том, что в митохондриях различных геномов происходит наибольшее количество нарушений второго правила Чаргаффа. Затем по степени нарушения второго правила Чаргаффа следуют геномы высших животных, в частности геном гориллы, далее можно выделить геномы внеклеточных форм жизни, в частности геном вируса табачной мозаики. Следующими нарушителями второго правила Чаргаффа являются грибковые организмы аскомицеты, затем – насекомые. Наименьшее нарушение второго правила Чаргаффа наблюдается для растений.

Данные таблицы свидетельствуют об экспоненциальном убывании невязки (1) с ростом толщины словаря для различных таксономических групп. Следует отметить, что вариабельность невязки при малых значениях толщины словаря весьма велика, но с ростом толщины словаря она падает, что согласуется с оценкой (6), произведённой выше. Наибольшее количество нарушений второго правила Чаргаффа среди исследованных нами организмов наблюдалось у митохондрий и внеклеточных форм жизни.

Справедливость оценки (6) подтверждается также рисунком, на котором показан ход значений отношения двух последовательных значений невязки (1), полученной для той или иной группы геномов. Хорошо видно, что по мере роста толщины словаря (при приближении толщины к q = 8) отношение двух последовательных значений невязки (1) стремится к значению, равному двум, что полностью согласуется с оценкой (6). По-видимому, можно ожидать, что точность приближения этого отношения к 2 будет лишь возрастать по мере роста толщины частотных словарей, взятых в рассмотрение.

Особого внимания заслуживает более детальное изучение поведения самой невязки (1) для сравнительно малых значений q: 1 ≤ q ≤ 4. Если стремление отношения двух последовательных значений невязки при росте q можно объяснить в том числе и эффектами конечности исследуемой символьной последовательности: действительно, число различных слов в частотном словаре растёт экспоненциально, что ведёт к быстрому падению числа тех слов, которые встречаются более чем в одной копии, – то поведение невязки на сравнительно малых длинах слов (1 ≤ q ≤ 4) скорее всего отражает биологические особенности анализируемых генетических последовательностей в наибольшей степени.

Величина невязки (1) для различных организмов; N1 – количество исследованных организмов; N2 – количество исследованных нуклеотидов, млн. пар; μmin – минимальное значение невязки; μmax – максимальное значение невязки; ⟨μ⟩ – среднее значение невязки σμ – стандартное отклонение

Представленные в статье результаты также косвенно опровергают одну из гипотез [1–4] происхождения второго правила Чаргаффа, а именно гипотезу удвоений. Согласно этой гипотезе, второе правило Чаргаффа возникло в результате серии удвоений длинных и сверхдлинных участков ДНК. При этом сама по себе последовательность, которая подвергалась удвоениям, предполагалась близкой по своим свойствам к случайной.

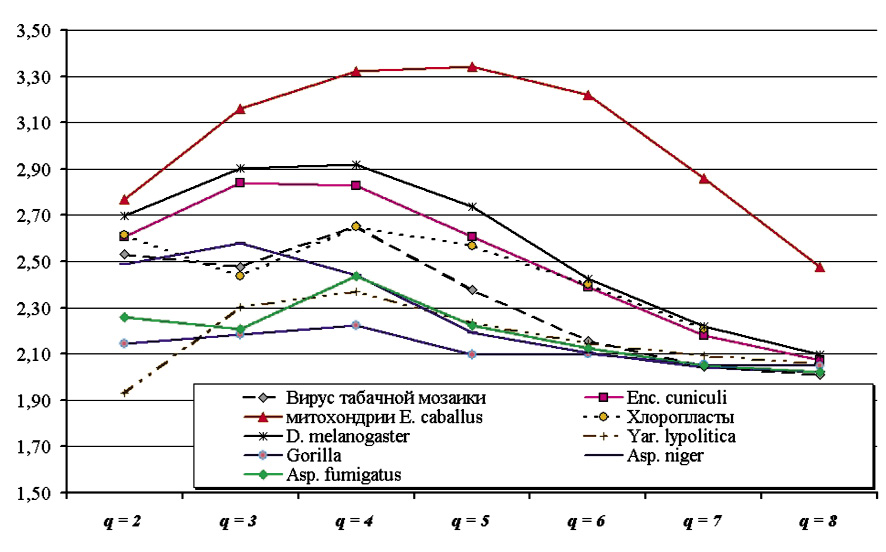
Отношение двух последовательных (по толщине словаря) значений невязки
для различных таксономических групп

Однако оценка (6) показывает, что для случайной последовательности – при условии почти точного выполнения второго правила Чаргаффа на уровне мононуклеотидного состава – второе правило Чаргаффа выполняется и для слов большей длины. Более того, можно ожидать, что длинные и сверхдлинные повторы будут приводить скорее к нарушениям второго правила Чаргаффа, по крайней мере в среднем по всей последовательности; возможно возникновение заметной гетерогенности последовательности по показателю невязки (1), определяемому для разных фрагментов исходной последовательности, однако этот вопрос выходит за рамки настоящей работы.

Садовский В.М., д.ф.-м.н., профессор, зав. лабораторным отделом вычислительной механики деформируемых сред Института вычислительного моделирования СО РАН, г. Красноярск;

Кратасюк В.А., д.б.н., профессор, зав. кафедрой биофизики ИФБиБТ СФУ, г. Красноярск.

Работа поступила в редакцию 19.12.2014.