В гибких производственных системах большинство манипуляционных функций может выполняться роботами и манипуляторами, обладающими высокоразвитыми исполнительными системами [1]. При выполнении технологических процессов обработки крупногабаритных изделий (демонтаж и монтаж ферм, резервуаров, объектов специального назначения и т.д.) в нестационарных условиях требуется максимальная концентрация различных технических устройств на подвижных носителях. Тогда роботизированный технологический центр должен представлять собой интегрированную систему с максимальной концентрацией операций и возможностью реализации технологического процесса практически в экстремальных условиях [2]. Примером такой системы является манипуляционная система лазер-робота «Палар-40», представленная на рис. 1 и состоящая из совокупности трех манипуляторов: транспортного и двух технологических, один из которых (основной) предназначен для перемещения рабочего инструмента при выполнении операции, а другой (дополнительный) – для идентификации обрабатываемой поверхности и ее подготовки к обработке.
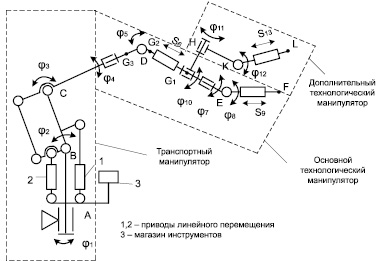
Рис. 1. Комплексированная манипуляционная система робота « Палар-40»
В процессе проектирования комплексированных манипуляционных систем с последовательным расположением транспортного и основного технологического манипуляторов (дополнительный манипулятор условно исключен) одной из задач является задача геометрического синтеза [3], в частности задача распределения длины совокупной кинематической цепи между ними. Это предопределяет разделение зоны работы Vp ∈ V6 на две зоны: V Р ТР ∈ VР и V Р Т ∈ VР, где V Р ТР и V Р Т – зоны работы транспортного и технологического манипуляторов. Отметим, что транспортный манипулятор является носителем для технологического и работает в режиме перестановки с фиксацией звеньев в положении статического равновесия во время работы технологического манипулятора.
Обозначим LТР и LТ – суммарные длины кинематических цепей транспортного и технологического манипуляторов соответственно – и сформулируем задачу, обозначенную выше. Для заданной рабочей зоны V ∈ V6 совокупной кинематической цепи манипуляторов, имеющих суммарную длину LТР + LТ = L = const, определить отношение K = LТР/LТ, которое бы доставляло минимум некоторому функционалу J при условии, что суммарное время T движения рабочей точки технологического манипулятора по некоторой траектории λ Î v (λ È c) и время перестановки транспортного было также минимальным.
В качестве функционала J будем рассматривать величину мощности, развиваемой манипуляторами, для перемещения рабочих точек в случае треугольной тахограммы движения [4], определенные условиями работы:
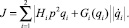(1)
Здесь Hip2qi, Gi(qi) – эквивалентные динамические и статические моменты манипуляторов;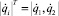 
– вектор обобщенных скоростей. Ввиду отсутствия количественных значений целого ряда параметров использование критерия в виде (1) предопределяет ряд допущений:
- звенья каждого из манипуляторов направлены вдоль одной прямой (рис. 2);
- центры масс манипуляторов находятся на середине их совокупных длин;
- рассматривается совокупность двух движений: перемещение рабочей точки технологического манипулятора (CC′ = C) и перемещение рабочей точки транспортного манипулятора (BB′);
- считаем, что в процессе движения непрерывно действуют статические и динамические моменты.
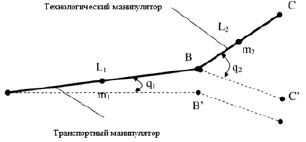
Рис. 2. Перемещения транспортного и технологического манипуляторов
Массы манипуляторов m1 и m2 зависят от их длины. Примем эту зависимость линейной:
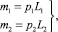(2)
где p1, p2 – массы единицы длины кинематических цепей манипуляторов. Учитывая, что
L2 = KL(K + 1)–1 и L1 = L(K + 1)–1,
выражение (1) можно привести к виду
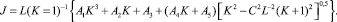(3)
В выражении (3) обозначено:
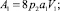
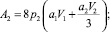
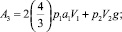
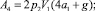
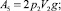V1, V2, a1, a2 – линейные скорости и ускорения центров масс; g – ускорение силы тяжести.
Анализ показывает, что функция J = Φ(K) в выражении (3) является знакопостоянной и возрастающей. Минимальное значение J определяется экстремалью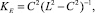 
в точке пересечения с которой величина Jmin равна:
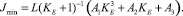(4)
Учитывая, что суммарное время движения манипуляторов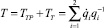 
, в соответствии с рис. 2 получим
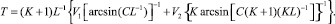(5)
Значение K = KT, доставляющее минимум величине Т, в явном виде из (5) выразить не удается в связи с трансцендентностью получающегося уравнения. Однако анализ выражения (5) показывает, что T = Tmin будет при выполнении условия
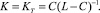(6)
Очевидно, что при любых значениях С и L КТ > Ке. Это означает, что с энергетической точки зрения отношение LТ/LТР должно быть большим, чем с динамической, оцениваемой быстродействием Т.
Поставим в соответствие значения
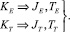(7)
Тогда количество перестановок транспортного манипулятора (количество участков работы технологического манипулятора) в течение некоторого достаточно большого интервала времени ТР безостановочной работы будет равно:
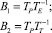(8)
Так как TT < TE, получим
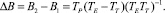
Дополнительные затраты энергии ΔE1 в случае K = KE для совершения количества циклов ΔB, отнесенные к одному циклу движения, равны:
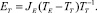
Тогда принятие значения K = KE по сравнению со значением KT по энергетическим затратам будет определяться из условия
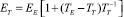
или после преобразования:
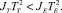(9)
Выражение (9) определяет соотношение действий [5] для двух сравниваемых вариантов. Выведенное неравенство позволяет проводить конкурсное сравнение различных вариантов построения манипуляторов (и других объектов) с энергетической точки зрения с учетом их быстродействия. При этом быстродействие оценивается не только как время потребления энергии от источника питания, но и как время выполнения заданной полезной работы.
Быстродействие в (9) учитывается лишь с энергетической точки зрения. В то же время в реальных условиях оно имеет самостоятельное значение и является важной технической характеристикой манипулятора, особенно в тех случаях, когда робот является «узким местом» в производственном процессе. Исходя из этого после несложных преобразований представим выражение (9) в виде
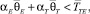(10)
где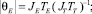 
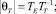
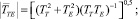
здесь αE и αT – экспертные весовые множители, определяемые, например, методом ранговой корреляции.
Выражение (10) представляет собой обобщенную энергодинамическую оценку различных вариантов построения исполнительной кинематической цепи манипуляторов и отражает соотношение между величиной потребляемой энергии и быстродействием, причем
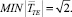
Выражения (9) и (10) могут быть использованы для конкурсной оценки энергетических и динамических характеристик различных технических объектов, осуществляющих периодические (циклические) движения.
На основании полученных аналитических выражений выполнено распределение параметров исполнительной кинематической цепи последовательно расположенных транспортного и технологического манипуляторов лазер-робота «Палар-40». Для вычислений приняты следующие исходные данные: L = 10 м; С = 1,5 м; p1 = 100 кг∙м–1; p2 = 50 кг∙м–1; V1 = 0,1 м∙с–1; V2 = 0,2 м∙с–1; a1 = 1 м∙с–2; а2 = 2 м∙с–2; g = 10 м∙с–2.
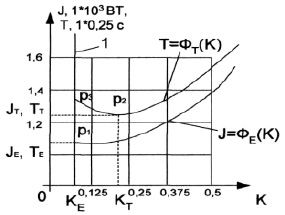
Рис. 3. Графики зависимостей J = ΦE(K) и T = ΦT(K) для манипуляторов лазер-робота «Палар-40»
На рис. 3 приведены графические зависимости J = ΦE(K) и T = ΦT(K), вычисленные в соответствии с выражениями (3) и (5). Прямая 1 – экстремаль, для которой КЕ = 0,076, КТ = 0,0203; JE = 1,13∙103 Вт; JT = 1,26∙103 Вт; ТЕ = 0,39 с; ТТ = 0,28 с.
Величину К определим, воспользовавшись выражением (9). Вычислим произведения: JTTT2 = 98,784 Вт с2; JЕTЕ2 = 171,873 Вт с2. Следовательно, в качестве искомой величины К следует принять K = KT = 0,203. Тогда длины кинематических цепей транспортного и технологического манипуляторов будут равны: LTP = 7,97 м; LT = 2,03 м.
Работа выполнена при финансовой поддержке РФФИ (проект № 13-08-01364).
Рецензенты:
Гоц А.Н., д.т.н., профессор кафедры тепловых двигателей и энергетических установок, Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, г. Владимир;
Кульчицкий А.Р., д.т.н., старший научный сотрудник, главный специалист ООО «Завод инновационных продуктов «КТЗ», г. Владимир.
Работа поступила в редакцию 18.11.2014