Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Оценка сложности учебного текста является важной проблемой теории обучения [4]. Ее решение требует учета дидактической сложности (ДС) входящих в него понятий. Из теории систем [3] следует, что сложность любой системы зависит от степени разнообразия, количества и сложности составляющих ее элементов. Текст представляет собой систему взаимосвязанных подсистем (предложений, понятий, формул, рисунков), каждая из которых также характеризуется своей сложностью [5]. Для оценки сложности понятий может быть использован метод парных сравнений, подробно рассмотренный в [1, 2, 6, 7].

Изучение физики предполагает овладение различными понятиями, которые обозначают физические объекты (вода, гравитационное поле, нейтрон), приборы и устройства (весы, амперметр, циклотрон), физические эксперименты (опыт Ома, опыт Столетова, опыт Физо), физические величины (импульс, интенсивность). Настоящая работа посвящена разработке эффективного метода оценки ДС понятий, обозначающих физические приборы, величины и эксперименты (или наблюдения), который позволяет получить значение ДС за небольшое количество шагов.

В теории познания выделяют внешний аспект объекта познания – явление и внутренний аспект – сущность, что соответствует делению естественно-научных знаний на эмпирические и теоретические. Физическая наука есть синтез теории и практики; любое физическое понятие может быть рассмотрено как с экспериментальной, так и с теоретической точек зрения. Поэтому логично предположить, что дидактическая сложность S физического понятия пропорциональна сумме двух характеристик:

1) возможности и сложности экспериментального изучения A учеником соответствующего прибора, эксперимента, физической величины;

2) сложности объяснения или теоретического изучения B сущности этого понятия.

Эти обе характеристики зависят от сложности структуры оцениваемого объекта, количества составляющих его элементов и связей между ними. Процедура определения ДС физического понятия не должна быть очень трудоемкой и занимать много времени, а погрешность оценки не должна превышать 10 %. Можно использовать формулу

S_i = a(A_i + B_i) + b,

где a и b подбираются так, чтобы ДС S_i лежала в интервале [0; 1], где 0 соответствует самому простому понятию, а 1 – самому сложному. С помощью метода парных сравнений можно точно оценить ДС 20–30 понятий из различных разделов физики и, расположив их в порядке возрастания, использовать получившийся список для оценки ДС других понятий, которые не подвергались анализу.

Дидактическая сложность физических приборов

Применяемую методику оценки ДС подробно рассмотрим на примере понятий, обозначающих физические приборы и устройства. На основе анализа школьных учебников был составлен список из N = 28 случайным образом выбранных механических, электрических, оптических и других приборов и устройств, начиная от линейки, весов и заканчивая циклотроном и ядерным реактором.

Для оценки возможности и сложности экспериментального изучения A и сложности теоретического изучения B использовался метод парных сравнений. В электронных таблицах Excel была создана таблица из N строк и N столбцов, содержащих сравниваемые понятия. Если вероятность того, что учащийся может самостоятельно использовать или наблюдать использование i-го прибора в повседневной жизни или в школе, меньше, чем j-го устройства, то Ai > Aj. В этом случае на пересечении i-й строки и j-го столбца ставится «1», а на пересечении j-й строки и i-го столбца ставится «–1». Если сложность обоих приборов (устройств) примерно одинакова, то в обе клетки таблицы ставятся нули. Можно уверенно утверждать, что понятия «масс–спектрограф», «осциллограф», «амперметр», «весы» расположены в порядке уменьшения характеристики A. Для нахождения Ai i-го понятия необходимо найти сумму всех элементов i-й строки Ai,sum, прибавить к ней некоторую постоянную и разделить на нормировочный коэффициент так, чтобы минимальное значение Ai было равно 0, а максимальное – 1.

Аналогичным образом осуществлялась оценка сложности B объяснения устройства и работы приборов. Можно представить ученика 6 класса, еще не изучавшего физику, либо человека, давно окончившего школу, которому объясняют устройство и принцип работы того или иного прибора, не демонстрируя его. Понятно, что чем сложнее прибор и физические принципы его функционирования, тем больше времени и усилий потребуется для объяснения. Некоторые приборы (весы) почти не требуют объяснений, другие (циклотрон) – предполагают довольно сложные рассуждения. Сложность объяснения принципа работы прибора (устройства) зависит от числа составляющих его элементов, сложности используемых моделей, понятий и законов, которые определяются характером происходящих процессов и взаимодействий. Механические устройства, как правило, проще тепловых, а те проще электрических и т.д. Если физические процессы расположить по возрастанию сложности, то получится ряд: механические, тепловые, электромагнитные и оптические, квантовые и ядерные.

Кроме оценки характеристик A и B с помощью таблиц Excel также использовался другой способ. На языке Pascal была написана компьютерная программа ПР-1, которая выводила на экран два сравниваемых понятия. Одно понятие – заранее заданное название i-го прибора, а другое – случайным образом выбранное понятие из входного файла, содержащего список из 28 физических приборов и устройств. Эксперт должен был сравнить оцениваемые качества этих двух приборов (то есть сложности A или B) и ввести с клавиатуры символы «+», «0» или «–», что соответствует «больше», «примерно одинаково», «меньше». Затем компьютер случайно выбирал следующее понятие и снова выводил его рядом с названием i-го прибора, а эксперт снова сравнивал оцениваемые качества этих понятий. После того, как i-е понятие было сопоставлено с каждым понятием из входного файла, результат помещался в выходной файл в виде строки «+ + + … +0 0 – + … – 0 + – –». В результате полного перебора всего списка приборов каждая пара понятий сравнивалась дважды, что позволило уменьшить влияние случайных факторов. Из этих строк вручную создавался текстовый файл, содержащий матрицу 28×28. Этот файл анализировался программой ПР-2, которая для каждой i-й строки находила сумму всех плюсов и из нее вычитала сумму всех минусов, получая результат xi. Аналогичная процедура осуществлялась со столбцами; для i-го столбца получалось yi. Величина оцениваемого качества считается пропорциональной разности xi – yi. К ней прибавлялась некоторая постоянная и результат умножался на коэффициент так, чтобы максимальное значение характеристики равнялось 1, а минимальное – 0. При этом использовались формулы

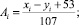
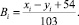
Таблица 1

Сводная таблица результатов оценки ДС приборов

Для нахождения дидактической сложности Si характеристики Ai, Bi складывались, а результат умножался на такой коэффициент, чтобы полученное значение Si находилось в интервале [0; 1], причем наименьшее S равнялось 0, а наибольшее – 1. Использовалась формула

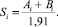
Результаты оценки характеристик Ai, Bi и дидактической сложности Si представлены в табл. 1; в ней понятия упорядочены по возрастанию Si. Связь между A и B характеризуется коэффициентом корреляции r_AB = 0,63. Из табл. 1 следует, что ДС конденсатора ощутимо меньше ДС трансформатора, но больше чем ДС весов, а циклотрон и интерферометр Майкельсона примерно одинаково сложны для изучения.

Дидактическая сложность физических величин

Аналогичным образом была произведена оценка дидактической сложности 26 величин из школьного курса физики. Предполагалось, что она пропорциональна сумме сложности объяснения (теоретического изучения) A и сложности (или возможности) измерения этой величины учеником B. Для оценки A и B также использовался метод парных сравнений, реализованный с помощью компьютерной программы. Полученный результат нормировался так, чтобы у самого простого понятия S = 0, а у самого сложного – S = 1.

Результаты оценки ДС физических величин представлены в табл. 2. Хотя они содержат величины с тремя значащими цифрами, погрешность составляет около 0,1. Оказалось, что между полученными оценками A и B имеет место слабая связь; коэффициент корреляции 0,43. На основе данных из табл. 1 и 2 нарисован рисунок. Полученные значения Si позволяют оценить дидактическую сложность понятий, не вошедших в табл. 1 и 2. Например, угол поворота – 0,0–0,1, напряженность электрического поля – 0,6–0,7, спектральная плотность излучения – 0,9, гальванический элемент – 0,3–0,4, ваттметр – 0,5–0,6 и т.д.

Дидактическая сложность физических экспериментов

При оценке дидактической сложности физических экспериментов можно исходить из той же модели «теория – практика». ДС понятия, обозначающего физический опыт или наблюдение, зависит от двух факторов:

1) сложности объяснения (теоретического изучения) A этого эксперимента (наблюдения), осуществляемого умозрительно, то есть без выполнения самого опыта;

2) сложности (или возможности) выполнения B рассматриваемого эксперимента учеником в повседневной жизни или на уроке.

Таблица 2

Сводная таблица результатов оценки ДС физических величин

При оценке сложности теоретического изучения A эксперт должен представить учителя, который описывает условия проведения опыта и объясняет его результат человеку, не изучавшему физику. Объяснение должно быть максимально кратким и опираться на формулы и законы, выделенные в стандартном учебнике в рамку и жирным шрифтом. Предполагается, что, объясняя опыт «демонстрация закона преломления света», учитель ссылается на закон преломления, а не на принцип Гюйгенса – Френеля, из которого этот закон может быть выведен. Сложность объяснения опыта зависит от количества элементов (приборов), составляющих экспериментальную установку, сложности используемых законов и понятий, степени абстрактности рассуждений, динамизма наблюдаемых явлений, необходимости использования воображения, математических моделей и абстрактных рассуждений. Понятно, что сложность объяснения опыта «кольца Ньютона» ощутимо выше, чем опыта «закон Ома».

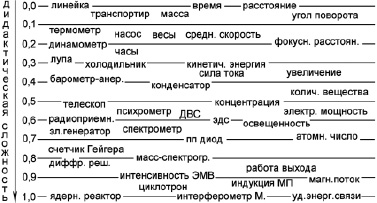
Результаты оценки дидактической сложности приборов и величин

Сложность и возможность выполнения B опыта учеником тем выше, чем меньше вероятность того, что среднестатистический ученик выполнит данный эксперимент дома или в школе. Эта характеристика зависит от количества и доступности используемых приборов и устройств. Ясно, эксперименты «измерение температуры тела», «односторонняя проводимость полупроводникового диода», «счетчик Гейгера», «работа ядерного реактора» расположены в порядке возрастания характеристики B.

Для определения A и B также использовался метод парных сравнений, реализованный с помощью описанной выше компьютерной программы. Оказалось, что оценки A и B связаны между собой: коэффициент корреляции между ними 0,58. ДС опыта рассчитывалась по формуле

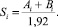
Если понятия расположить в порядке возрастания сложности S, используя формат «название i-го опыта (наблюдения), (Ai; Bi) – Si», то получится следующая последовательность:

1) измерение температуры термометром (0; 0,008) – 0,00;

2) измерение массы весами (0,061; 0,0)  – 0,03;

3) тепловое расширение твердых тел (шар Гравезанда) (0,183; 0,023) – 0,11;

4) изучение закона Гука для пружины, резины (0,168; 0,077) – 0,13;

5) определение силы Архимеда динамометром (0,137; 0,115) – 0,13;

6) измерение плотности ареометром (0,168; 0,131) – 0,16;

7) диффузия медного купороса (0,183; 0,138) – 0,17;

8) зависимость периода колебаний математического маятника от длины (0,191; 0,182) – 0,20;

9) измерение влажности психрометром (0,382; 0,246) – 0,33;

10) измерение g на машине Атвуда (0,290; 0,492) – 0,41;

11) закон преломления (шайба Гартли) (0,405; 0,385) – 0,41;

12) опыт Кулона (0,473; 0,354) – 0,43;

13) наблюдение броуновского движения (0,771; 0,154) – 0,48;

14) дисперсия света (Ньютон) (0,397; 0,538) – 0,49;

15) электролиз медного купороса (0,481; 0,523) – 0,52;

16) электромагнитная индукция (опыты Фарадея) (0,389; 0,615) – 0,52;

17) односторонняя проводимость полупроводникового диода (0,321; 0,692) – 0,53;

18) опыты с кольцом Ленца (индукционный ток) (0,374; 0,646) – 0,53;

19) работа трансформатора (0,489; 0,723) – 0,63;

20) камера Вильсона (0,771; 0,477) – 0,65;

21) затухающие колебания в колебательном контуре (с осциллографом) (0,588; 0,677) – 0,66;

22) опыт Кавендиша по измерению G (1,0; 0,292) – 0,67;

23) кольца Ньютона (0,412; 0,885) – 0,68;

24) счетчик Гейгера (0,748; 0,631) – 0,72;

25) измерение скорости света Физо (0,992; 0,40) – 0,73;

26) усилительные свойства транзистора (0,550; 0,846) – 0,73;

27) измерения скорости света Ремером (0,977; 0,438) – 0,74;

28) резонанс электромагнитных колебаний в LC-контуре (0,634; 0,815) – 0,75;

29) детекторный радиоприемник (0,565; 1,00) – 0,82;

30) фотоэффект (опыт Столетова) (0,656; 0,923) – 0,82;

31) поляризация ЭМВ (СВЧ генератор с рупорной антенной) (0,756; 0,831) – 0,83;

32) опыт Резерфорда (строение атома) (0,985; 0,615) – 0,83;

33) отклонение альфа-, бета- и гамма-лучей в МП (0,977; 0,70) – 0,87;

34) работа масс-спектрографа (0,893; 0,854) – 0,91;

35) ядерный взрыв, неуправляемая ядерная реакция (0,992; 0,777) – 0,92;

36) работа циклотрона (0,992; 0,923) – 1,0;

37) работа ядерного реактора (0,985; 0,938) – 1,0.

Заключение

В настоящей работе рассмотрены результаты оценки дидактической сложности понятий, обозначающих физические приборы, величины и физические эксперименты (наблюдения), которая основана на использовании метода парных сравнений [1, 2, 6, 7]. Автору не известны работы, в которых была бы решена эта проблема. Так как каждое понятие сравнивалось с более чем 25 другими понятиями, выбранными случайно, то полученные результаты имеют погрешность не более 0,1. Они могут применяться для определения дидактической сложности других понятий, обозначающих физические приборы и величины. Для этого их необходимо сравнить с понятиями, сложность которых уже определена. Все это может быть использовано для оценки сложности изучаемого материала, учебного текста и т.д.

Рецензенты:

Казаринов А.С., д.п.н., профессор кафедры информатики, теории и методики обучения информатике, ФГБОУ ВПО «Глазовский государственный педагогический институт им. В.Г. Короленко», г. Глазов;

Саранин В.А., д.ф.-м.н., профессор кафедры физики и дидактики физики, ФГБОУ ВПО «Глазовский государственный педагогический институт им. В.Г. Короленко», г. Глазов.

Работа поступила в редакцию 17.10.2014.