Широкое применение в современных машинах имеют механизмы с гидро- и пневмоцилиндрами, которые могут быть приведены к кинематической схеме кулисного механизма [1, 2]. Поэтому исследование динамики кулисного механизма является актуальной задачей. Первым этапом в таких исследованиях является кинематический анализ, задача которого заключается в установлении зависимостей между кинематическими параметрами звеньев механизма. Среди аналитических методов кинематического анализа в теории механизмов и машин наибольшее распространение получили метод векторных контуров, разработанный В.А. Зиновьевым [2], метод преобразования координат, развитый в работах Г.Ф. Морошкина [4], а также графические и аналитические методы кинематического анализа плоских механизмов [3, 5]. В работе [5] получены кинематические зависимости, необходимые для динамического анализа кулисного механизма с одной степенью свободы с неподвижными вращательными кинематическими парами.
Целью данной работы является разработка математической модели динамики кулисного механизма, а также определение законов движения механизма в обобщенных координатах. В работе приводятся результаты решения частных задач при различных начальных условиях.
Рассматривается кулисный механизм (рис. 1) с одной степенью свободы, образованный замкнутой кинематической цепью с тремя подвижными звеньями. Кривошип 1 и кулиса 2 образуют со стойкой неподвижные вращательные кинематические пары O1 и O2.
Исходными данными для исследования динамики механизма являются длина кривошипа l, координаты неподвижных кинематических пар x1, y1 (пара O1) и x2, y2 (пара O2), а также массы и моменты инерции звеньев.
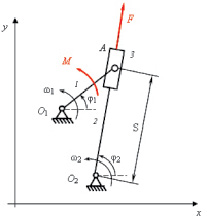
Рис. 1. Кинематическая схема механизма: 1 – кривошип; 2 – кулиса; 3 – кулисный камень
Система имеет одну степень свободы. Для определения закона движения системы составим уравнение Лагранжа II рода [6]:
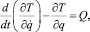(1)
где q – обобщенная координата системы; 
– обобщенная скорость; Q – обобщенная сила; T – кинетическая энергия системы.
Кинетическая энергия механизма определяется как сумма кинетических энергий его подвижных звеньев:
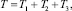(2)
где T1, T2, T3 – кинетические энергии кривошипа, кулисы и кулисного камня.
Выражения для кинетических энергий имеют вид [6]:
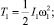
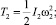
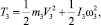
где I1 – момент инерции кривошипа относительно оси вращения; I2 – момент инерции кулисы относительно оси вращения; I3 – момент инерции кулисного камня относительно оси, проходящей через его центр масс A и перпендикулярной к плоскости движения механизма; m3 – масса кулисного камня; ω1, ω2, ω3 – угловые скорости кривошипа, кулисы и кулисного камня; VA – скорость центра масс кулисного камня.
Рассмотрим случай, когда движение механизма вызвано активным постоянным вращающим моментом M, действующим на кривошип (рис. 1).
В качестве обобщенной координаты выберем угол поворота кривошипа q = φ1, тогда обобщенная скорость представляет собой угловую скорость кривошипа
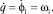
Кинематическая зависимость для угловой скорости кулисы приведена в работе [5] и в обобщенных координатах принимает вид
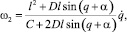(3)
где C, D и α определяются выражениями
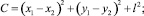
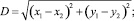
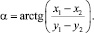
Скорость центра масс кулисного камня определяется выражением
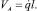
Учитывая, что ω2 = ω3, для кинетической энергии системы получено следующее выражение:
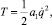(4)
где a1 – коэффициент инерции, соответствующий выбранной обобщенной координате q = φ1, определяется выражением
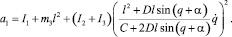
Производные от кинетической энергии, образующие левую часть уравнения Лагранжа.II рода (1), определяются выражениями
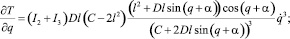(5)
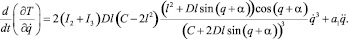(6)
Правая часть уравнения Лагранжа представляет собой обобщенную силу. Если движение механизма вызвано действием только вращающего момента M, а другие активные силы и моменты отсутствуют, то
Q = M. (7)
Подставляя выражения (5), (6) и (7) в уравнение Лагранжа II рода (1), получим дифференциальное уравнение движения механизма в обобщенных координатах, для рассматриваемого случая;
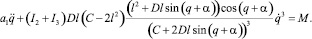(8)
Выразим угловое ускорение кривошипа
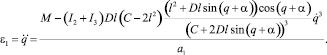(9)
Рассмотрим случай, когда движение механизма вызвано активной постоянной по величине силой F, действующей на кулисный камень (рис. 1).
В качестве обобщенной координаты выберем перемещение кулисного камня в относительном движении q = S, тогда обобщенная скорость представляет собой относительную скорость кулисного камня
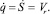
Кинематические зависимости для угловых скоростей кривошипа и кулисы приведены в работе [5] и в обобщенных координатах принимают вид
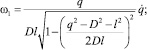(10)
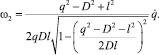(11)
Скорость центра масс кулисного камня определяется выражением
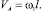
Учитывая, что ω2 = ω3, для кинетической энергии системы получено следующее выражение:
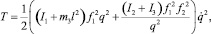(12)
где f1 и f2 ‒ функции обобщенных координат, которые определяются выражениями
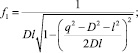
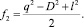
Представим кинетическую энергию в виде
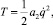(13)
где a2 – коэффициент инерции, соответствующий выбранной обобщенной координате q = S, определяется выражением
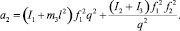
Производные от кинетической энергии, образующие левую часть уравнения Лагранжа II рода (1), определяются выражениями
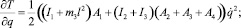(14)
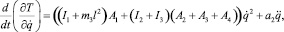(15)
где функции A1, A2, A3, и A4 определяются по формулам
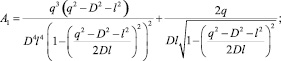
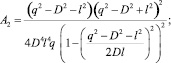
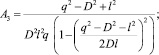
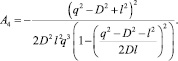
Если движение механизма вызвано действием постоянной по величине силы F, а другие активные силы и моменты отсутствуют, то
Q = F. (16)
Подставляя выражения (14), (15) и (16) в уравнение Лагранжа II рода (1), получим дифференциальное уравнение движения механизма в обобщенных координатах, для рассматриваемого случая:
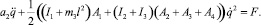(17)
Выразим относительное ускорение кулисного камня:
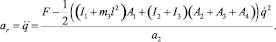(18)
Дифференциальные уравнения движения в обобщенных координатах (8) и (17) могут быть использованы для определения законов движения системы в обобщенных координатах и кинематических характеристик звеньев механизма. Для решения уравнений могут быть использованы различные численные методы.
Рассмотрим результаты решения, полученные при реализации метода Рунге ‒ Кутта четвертого порядка. На рис. 2 представлены зависимости углов поворота кривошипа φ1 и кулисы φ2 от времени t, а также закон относительного движения кулисного камня в случае, когда движение механизма вызвано постоянным вращающим моментом M. На рис. 3 представлены эти же зависимости в случае, когда движение механизма вызвано постоянной по величине силой F, действующей на кривошип (рис. 1). Представленные зависимости получены при следующих исходных данных и начальных условиях:
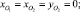
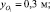l = 0,1 м;
t0 = 0; φ1(t0) = 0; S(t0) = 0,316228 м;
ω1(t0) = 0; Vr(t0) = 0;
M = 3 Н∙м; F = 1 Н;
m3 = 0,3; I1 = 0,0016667 кг∙м2;
I2 = 0,00004 кг∙м2; I3 = 0,0833333 кг∙м2.
а 
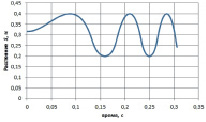б
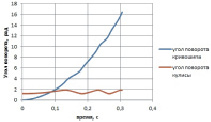
Рис. 2. Кинематические характеристики механизма, при действии постоянного вращающего момента M: а – зависимость углов поворота кривошипа φ1 и кулисы φ2 от времени; б – закон относительного движения кулисного камня
а 
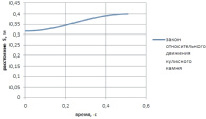б
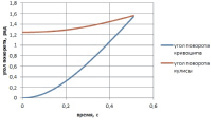
Рис. 3. Кинематические характеристики механизма, при действии на кулисный камень силы F: а – зависимость углов поворота кривошипа φ1 и кулисы φ2 от времени; б – закон относительного движения кулисного камня
Заключение
Анализ графиков зависимостей кинематических характеристик от времени (рис. 2), полученных для случая, когда движение механизма вызвано действием на кривошип постоянного вращающего момента M, показывает, что движения кулисы и кулисного камня носят колебательный характер, с возрастающей частотой.
Полученные дифференциальные уравнения движения механизма в обобщенных координатах (8) и (17) могут быть использованы для решения задач при различных исходных данных и начальных условиях, в том числе и в случаях, когда движение механизма вызвано действием переменных нагрузок.
Результаты работы могут быть использованы для разработки математических моделей динамики кулисных механизмов и разработки алгоритмов автоматизации соответствующих расчетов.
Рецензенты:
Панов А.Ю., д.т.н., заведующий кафедрой «Теоретическая и прикладная механика», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород;
Иванов А.А., д.т.н., профессор кафедры «Автоматизация машиностроения», ФГБОУ ВПО «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Работа поступила в редакцию 17.10.2014.