В настоящее время актуальной является задача технического перевооружения предприятий отечественного машиностроения, направленная на повышение конкурентоспособности российской промышленности. Основой такого перевооружения является комплексная автоматизация процессов управления, а также всемерное повышение эффективности производства за счет использования передовых технологий. Применение новых прогрессивных технологий дает мощный потенциал для повышения производительности труда, снижения энерго- и ресурсопотребления, повышения качества выпускаемой продукции.
В современных условиях к прогрессивным технологиям можно отнести такое производство, которое динамично и на высоком уровне качества реагирует на возникающие задачи. Прогнозируя развитие промышленного производства и анализируя научно-технические разработки, можно предположить, что к такому роду производства можно отнести гибкие производственные системы (ГПС), которые наилучшим образом удовлетворяют требованиям заказчика и производителя, повышают конкурентоспособность предприятий, обеспечивая высокую эффективность и рентабельность производства, снижая затраты на энергоносители и энергоемкие ресурсы. Такой тип производства должен работать эффективно по оптимальному принципу «делай вовремя», так как поставки комплектующих изделий осуществляются строго в определенное время.
Требования к ускорению обновлений продуктовой линейки предполагают переход машиностроения от автоматизации частных элементов производственного процесса к комплексной автоматизации на всех уровнях, применению ГПС в условиях единичного, серийного и массового производств. Такой подход открывает путь к решению сложившихся противоречий между высокой производительностью и отсутствием мобильности производственного оборудования массового производства, высокой мобильностью и низкой производительностью универсальных станков единичного и серийного производств.
Основой для решения сложности и противоречивости поставленных задач являются частные свойства гибких производственных систем, а именно: возможность оперативной перенастройки за счет гибкости и мобильности; высокий технический уровень оборудования; высокая степень интеграции производства; обеспечение конкурентоспособности и рентабельности выпускаемой продукции.
В том числе ГПС позволяют решать комплексные вопросы по улучшению условий труда работающих, обеспечивая постепенное стирание граней между умственным и физическим трудом, освобождают исполнителей от тяжелого физического труда, стимулируют повышение профессионального уровня работающих, создают объективные условия для повышения производительности труда.
В настоящей статье уделяется особое внимание проблемам организации эффективного распределения пропускной способности магистрали сети между всеми подключенными абонентами и минимизации аппаратных затрат на организацию связи. Рассмотрим нижний уровень автоматизации системы на примере распределенной системы управления линии микрофотолитографии [1].
На нижнем уровне автоматизированной системы управления гибкими производственными модулями возникает необходимость обеспечить:
1) высокую производительность и надежность работы;
2) эффективное распределение пропускной способности магистрали сети передачи данных между ЭВМ (обслуживающим прибором) и всеми подключенными модулями (абонентами сети);
3) выполнение процесса обмена данными и сигналами управления с минимальными затратами на аппаратную организацию связи;
4) ориентацию коммуникационного протокола связи на технологическую специфику производства;
5) минимальную функциональную избыточность протокола связи.
Заявки от абонентов сети перемещаются от входа к выходу системы обслуживания требований в соответствии с установленными законами управления, задаваемыми дисциплинами ожидания и обслуживания. Дисциплина ожидания определяет очередность приема требований в систему и порядок расположения их в очереди, дисциплина обслуживания задает порядок выбора заявок из очереди для назначения на обслуживание. В зависимости от принятого порядка обработки заявок различают системы с бесприоритетными и приоритетными дисциплинами.
Системы с бесприоритетными дисциплинами определяют заявки от абонентов как равноправные. В качестве примера можно привести следующие правила выборки заявок из очереди при необходимости назначения на обслуживание:
1) дисциплина FIFO (First Input – First Output) – «Первым пришел – Первым вышел» – выбирается первая в очереди заявка;
2) дисциплина LIFO (Last Input – First Output) – «Последним пришел – Первым вышел» – выбирается последняя в очереди заявка;
3) дисциплина выбора заявки из очереди случайным образом.
В приоритетных дисциплинах обслуживания определенным заявкам одного типа предоставляется преимущественное право на обслуживание перед заявками другого типа, в соответствии с установленным приоритетом.
Различают следующие типы приоритетов:
1) относительные приоритеты – учитываются только в момент назначения заявки на обслуживание. При освобождении канала обслуживания сравниваются приоритеты заявок, находящихся в очереди в состоянии ожидания, и обслуживание предоставляется заявке с наибольшим приоритетом, после чего выбранная заявка захватывает канал обслуживания;
2) абсолютные приоритеты предполагают прерывание обслуживания низкоприоритетной заявки в момент поступления в систему массового обслуживания (СМО) заявки с более высоким приоритетом, прерванная заявка ставится в начало либо общей очереди, либо очереди заявок соответствующего приоритета;
3) смешанные приоритеты предполагают сочетание рассмотренных видов приоритета, причем для отдельных заявок может быть использовано бесприоритетное обслуживание.
При подключении абонентов к магистрали ЭВМ используется совмещенная шина данных, через которую в каждый момент времени осуществляется передача данных от одного абонента к ЭВМ или прием сообщения со стороны ЭВМ от выбранного в соответствии с установленной дисциплиной обслуживания абонента.
Для N абонентов сети при использовании дисциплин с равноправным или с приоритетным обслуживанием используются отдельные N линий, обеспечивающих поступление в ЭВМ требований на обслуживание от каждого абонента в отдельности.
Обслуживающий прибор выполняет, как правило, поиск активных требований на обслуживание двумя способами:
1) номера требований опрашиваются, начиная с младших номеров, при нахождении i-го активного требования выполняется обслуживание i-го абонента, затем поиск продолжается с (i + 1)-го номера. При достижении максимального номера i = N опрос требований продолжается с младшего номера i = 1. Такой вариант поиска запросов реализует обслуживание требований с использованием дисциплины с равноправными приоритетами (ДРП);
2) номера требований сканируются, начиная с младших номеров, при нахождении i-го активного требования выполняется обслуживание i-го абонента, затем поиск продолжается с младшего номера i = 1. При достижении i = N опрос требований продолжается с младшего номера i = 1. Такой вариант поиска запросов реализует обслуживание требований в соответствии с дисциплиной с относительными приоритетами (ДОП).
Для модели системы с ДОП требование обслуживается в приборе до конца без прерывания, после чего из очереди берется требование с наименьшим номером. Требования одного приоритетного уровня образуют изолированную очередь соответствующего уровня приоритета. Порядок обслуживания внутри такой очереди осуществляется в порядке поступления требований. Модель такой системы предполагается без потерь с неограниченным числом мест в очереди.
Для системы с дисциплиной с относительными приоритетами среднее время ожидания сообщений с приоритетом r можно найти по следующей формуле [2]:
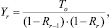(1)
где
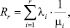(2)
λi – средняя интенсивность поступления заявок i-го приоритета; μi – средняя интенсивность обслуживания заявок i-го приоритета; To – среднее время завершения текущего обслуживания заявки в ЭВМ (приборе).
С целью сокращения количества аппаратных затрат с N линий, по которым от N абонентов поступают соответствующие требования на обслуживание к ЭВМ, до одной интегрированной линии предлагается следующее схемотехническое решение [3, 4, 5]. При данном подходе к ЭВМ поступает только одна линия, по которой формируется интегрированный запрос требования на обслуживание лишь в том случае, если в системе присутствуют один или несколько активных абонентов, требующих обмена данными (рис. 1). При этом со стороны ЭВМ не требуется проводить опрос абонентов для выбора наиболее активного источника с учетом установленной дисциплины обслуживания. Схемотехническое решение автоматически реализует обслуживание абонентов с предлагаемой дисциплиной выравнивания приоритетов (ДВП). Для оценки эффективности предлагаемого решения рассмотрим математическую модель системы с ДВП.
В систему обслуживания требований поступает N классов заявок. Класс заявки определяется порядковым номером расположения абонента относительно ЭВМ (обслуживающего прибора). Запросы r-го абонента образуют очередь требований к магистрали сети (рис. 1) для их последующей передачи в соответствующий буферный регистр (БР.r) и включения в очередь требований на обслуживание к ЭВМ. Каждый буферный регистр БР.r и элемент очереди Gr.i (где i – порядковый номер элемента Gr в очереди требований r-го абонента к магистрали сети) предназначены для хранения одной порции информации (пакета или сообщения).
При построении математической модели СМО требований будем считать, что:
1) поток заявок со стороны абонентов образует пуассоновский процесс с параметром λ;
2) длительность обслуживания подчиняется экспоненциальному закону со средним значением, равным 1/μ;
3) если в момент поступления требования очередь данного класса заявок занята, то требование теряется.
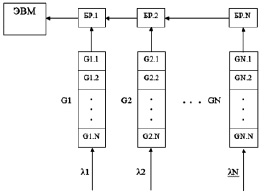
Рис. 1. Система обслуживания с N классами заявок
Сформулируем алгоритм обработки требований различного класса в СМО с предлагаемой дисциплиной выравнивания приоритетов.
Правило, регламентирующее включение элемента Gr.1 в очередь требований на обслуживание к ЭВМ, определяется выполнением следующих условий:
1) условие 1 – запрос Gr.1 из очереди требований к магистрали сети будет поставлен в соответствующий буферный регистр БР.r, если последний свободен от наличия в нем другого требования;
2) условие 2 – запрос Gr, поставленный в буферный регистр БР.r, будет включен в очередь требований на обслуживание к ЭВМ при отсутствии других запросов, включенных в очередь требований на обслуживание к ЭВМ, с более старшими порядковыми номерами по отношению к данному классу требований (j = r + 1,…, N).
3) условие 3 – одновременное появление двух и более запросов от абонентов различного класса, для которых выполняются условия 1 и 2, вызывает их безусловное включение в очередь требований на обслуживание к ЭВМ.
Сформулируем правило, регламентирующее порядок обслуживания запросов, включенных в очередь требований на обслуживание к ЭВМ:
4) условие 4 – включенный в очередь требований на обслуживание к ЭВМ запрос будет обработан лишь после того, как будут обслужены все другие запросы от абонентов с младшими порядковыми номерами (j = 1,…, r – 1) по отношению к данному классу, включенные в очередь требований на обслуживание к ЭВМ.
В соответствии с данным алгоритмом процесс передачи сообщения r-го абонента ЭВМ можно разбить на три этапа:
1) включение запроса в очередь требований к ЭВМ;
2) ожидание начала обслуживания запроса в очереди требований к ЭВМ;
3) непосредственное обслуживание запроса ЭВМ (прибором).
Рассмотрим требование класса r. Требование поступает в систему в момент времени tо и через Wr единиц времени (рис. 2) поступает на обслуживание (начинается передача сообщения) в момент времени t1. Необходимо получить общее соотношение для Wr – среднего времени ожидания обслуживания требования класса r.
Определим слагаемые, из которых складывается Wr:
1) среднее время Tо, необходимое для завершения текущего обслуживания запроса в ЭВМ;
2) среднее время Тr обслуживания Nr требований класса r, ожидающих обслуживание в очереди к моменту поступлений рассматриваемого запроса;
3) среднее время Тожид.r ожидания заявки из r-й очереди обслуживания всех тех заявок j-го класса (где r, j = 1,.., N; j ≠ r), которые в течение времени Wr будут включены в очередь требований на обслуживание к ЭВМ и обработаны в соответствии с реализуемой дисциплиной ДВП.
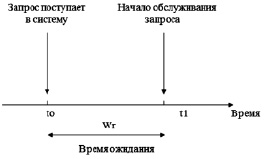
Рис. 2. Время ожидания в системе обслуживания
Для оценки Тr допустим, что среднее число ожидающих требований класса r составляет Nr. Если каждое из требований требует для обслуживания в среднем tr = 1/µr единиц времени, то
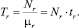(3)
Но Nr представляет собой разность двух величин – среднего числа требований, ожидающих и обслуживаемых в системе Mr, и среднего числа обслуживаемых в системе требований, число которых составляет ρr = λr/μr, где λr – интенсивность потока требований r-го класса.
Из теоремы Литтла [6] следует:
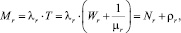(4)
где Т – среднее время задержки.
Следовательно,
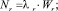(5)
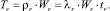(6)
Среднее время дообслуживания заявки из суммарного потока Tо не зависит от порядка обслуживания и для определенной системы массового обслуживания постоянно 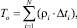[7]:
(7)
где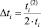 
– среднее время дообслуживания i-й заявки, если она находится в ЭВМ (обслуживающем приборе); 
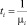– среднее время обслуживания заявки; 
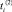– второй момент среднего времени обслуживания заявки.
При показательном распределении обслуживания [8]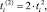 
поэтому время To можно выразить как
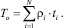(8)
Таким образом, для определения среднего времени ожидания заявкой i-го класса начала обслуживания со стороны ЭВМ необходимо решить систему уравнений из N – числа абонентов в сети:
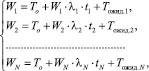(9)
Данную систему линейных уравнений в таком виде решить невозможно, так как число неизвестных параметров (Wi, Tожид.i) превышает количество уравнений в системе (9) в два раза.
Значения Wi, приводящие к решению системы уравнений (9), должны удовлетворять закону сохранения накопленной в очереди предстоящей работы [6]:
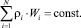(10)
Величина (10) не зависит от нумерации приоритетов в системе и равна накопленной в очереди работе в бесприоритетной СМО, поэтому для ДРП справедливо следующее выражение:
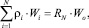(11)
где
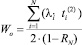, (12)
и при пуассоновских входящих потоках
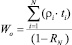, (13)
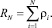(14)
Среднее время ожидания заявки из r-й очереди Tожид.r можно представить в следующем виде:
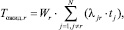(15)
где λjr – средняя интенсивность включения заявок j-го класса в очередь требований на обслуживание к ЭВМ в единицу времени с вытеснением заявок r-го приоритета в фазу ожидания или средняя интенсивность поступления в систему заявок j-го класса, которые будут включены в очередь требований к ЭВМ и обработаны обслуживающим прибором прежде требования r-го абонента (r ≠ j), находящегося в буферном регистре БР.r, но ожидающего выполнение условия 2 постановки в очередь требований к ЭВМ или включенного в очередь требований к ЭВМ, но ожидающего обслуживания в соответствии с условием 4; tj – среднее время обслуживания прибором заявки j-го класса; (λjr·tj) – средняя очередь заявок со стороны j-го абонента, которая образуется за время Wr ожидания обслуживания требования класса r и будет освобождена до ее поступления в ЭВМ;
(Wr·λjr·tj) – среднее время обслуживания этой очереди.
Тогда систему уравнений (9) можно представить в следующем виде:
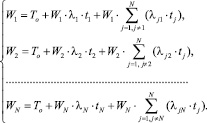(16)
Для решения системы (16) введем величину ρjr = λjr·tj, которая выражает среднее число переключений обслуживающего прибора в единицу времени на обработку заявок j-го класса (r, j = 1,…, N; r ≠ j) при наличии требования r-го абонента, находящегося в буферном регистре БР.r, но ожидающего выполнения условия 2 постановки в очередь требований к ЭВМ или включенного в очередь требований к ЭВМ, но ожидающего обслуживания в соответствии с условием 4.
Переключающий поток с интенсивностью λjr является просеянным относительно входного потока λj с некоторой вероятностью переключения Рпер.jr и в соответствии с известной теоремой [6] о просеянном потоке соответствует пуассоновскому характеру распределения. Заявки переключающего потока λjr обрабатываются прибором в порядке их поступления, а длительность обслуживания заявок подчиняется экспоненциальному закону со средним значением, равным 1/µj.
Принятые условия позволяют применить известную формулу СМО M/M/1 для определения средней очереди переключения обслуживающего прибора на обработку заявок j-го класса (r, j = 1,…, N; r ≠ j) при наличии требования r-го абонента, находящегося в буферном регистре БР.r, но ожидающего выполнения условия 2 постановки в очередь требований к ЭВМ или включенного в очередь требований, но ожидающего обслуживание в соответствии с условием 4:
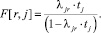(17)
Из выражения (17) получим значение интенсивности переключающего потока λjr:
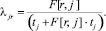(18)
Для определения средней очереди переключения обслуживающего прибора F[r, j] для каждого класса заявок (r, j = 1,…, N; r ≠ j) необходимо построить математическую модель, описывающую стационарный режим работы системы с использованием марковского случайного процесса. Используя диаграмму или таблицу интенсивностей переходов, составим систему линейных уравнений равновесия, из решения которых определим значения стационарных вероятностей Pk. При этом значение F[r, j] будет равно
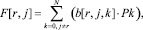(19)
где Pk – вероятность нахождения системы в k-м стационарном состоянии; b[r, j, k] – среднее число переключений обслуживающего прибора на обработку заявок j-го класса (r, j = 1,…, N; r ≠ j) при наличии требования r-го абонента, находящегося в буферном регистре БР.r, но ожидающего выполнения условия 2 постановки в очередь требований к ЭВМ или включенного в очередь требований к ЭВМ, но ожидающего обслуживания в соответствии с условием 4 для случая нахождения системы в k-м стационарном состоянии.
Подставляя полученные значения F[r, j] в выражения (18), а затем в (16), получаем решение системы относительно неизвестных параметров W1, W2, …, WN, что позволяет сравнить полученные результаты с соответствующими величинами среднего времени ожидания Y1, Y2, …, YN для заявок в системе с дисциплиной относительных приоритетов ДОП:
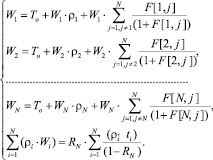(20)
Для сравнения предлагаемой дисциплины ДВП с дисциплиной ДОП по критерию равноправного обслуживания в качестве базовой модели выбрана модель бесприоритетной СМО (13) с N типами заявок по числу абонентов, которые обрабатываются прибором в порядке их поступления.
Введем коэффициент равноправного обслуживания Kf, определяющий степень приближения времени ожидания обработки заявок разного класса приоритетов в исследуемой СМО к времени ожидания обработки заявок в бесприоритетной системе:
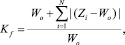(21)
где Wo – среднее время ожидания обслуживания заявок для бесприоритетной СМО с N типами заявок по количеству абонентов; f – индекс, задающий тип дисциплины обслуживания:
1) если f = w, то величина Zi = Wi и определяется в соответствии с выражением (20);
2) если f = y, то величина Zi = Yi и определяется в соответствии с (1);
3) если f = о, то величина Zi = Wo и определяется в соответствии с (13).
Из выражения (21) видно, что при Kf → 1 время обработки заявок разного класса в системе близко по параметрам к времени обработки заявок в бесприоритетной СМО, т.е. рассматриваемая система стремится к более равноправной процедуре обслуживания по отношению ко всем подключенным абонентам вне зависимости от их месторасположения по отношению к ЭВМ (обслуживающему прибору).
Для сравнения СМО по критерию эффективности работы [2, 9] будем использовать коэффициент Gf, который выражает стоимость пребывания всех заявок в единицу времени в системе:
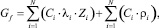(22)
где Ci – стоимость пребывания заявки i-го абонента в единицу времени в системе; f – индекс, задающий тип дисциплины обслуживания.
Если установить все C = 1, то коэффициент G будет равным среднему числу заявок в СМО. Таким образом, чем меньше коэффициент G, тем более эффективной будет рассматриваемая система массового обслуживания.
Из теории СМО известно [10, 11], что, когда загрузка оборудования превышает 80–90 %, то незначительное увеличение трафика может привести к резкому спаду производительности системы или даже перевести систему в аварийный режим. Поэтому, анализ модели СМО с ДВП для нескольких источников заявок проведем на интервале нагрузки (0 < ρ ≤ 0,9).
Проведенное исследование с помощью разработанной математической модели СМО (в научно-исследовательском институте полупроводникового машиностроения «НИИПМ», г. Воронеж) с предлагаемой дисциплиной выравнивания приоритетов для систем, в которых критичным параметром является время ответа, показывает [12] повышение резерва производительности системы на 15–20 %.
Выводы
Проведенные исследования позволяют сделать следующие обоснованные и подтвержденные выводы:
1. В современных условиях при построении нижнего уровня автоматизированной системы управления гибкими производственными модулями важны в первую очередь такие показатели, как высокая производительность и надежность работы системы, минимальные затраты на аппаратную организацию связи, эффективное распределение пропускной способности магистрали сети передачи данных между ЭВМ и всеми подключенными модулями.
2. Поскольку при организации распределенных систем с дисциплинами равноправного или приоритетного обслуживания возникает необходимость использования и сканирования со стороны ЭВМ N независимых линий запросов требований на обслуживание от каждого подключенного модуля, то, в целях снижения аппаратных затрат, предложено схемотехническое решение, позволяющее сократить число линий до одной, по которой формируется интегрированный запрос требования на обслуживание.
3. Представлен алгоритм дисциплины обслуживания выравнивания приоритетов, регламентирующий порядок включения запроса в очередь требования на обслуживание к ЭВМ и порядок обслуживания запроса в этой очереди, позволяющий выровнять приоритеты заявок, вне зависимости от их месторасположения к ЭВМ.
4. Разработанная математическая модель системы массового обслуживания с дисциплиной выравнивания приоритетов показывает для систем определенного класса, работающих в условиях высокой загрузки оборудования свыше 80–90 %, в которых критичным параметром является минимальное время ответа, повышение резерва производительности на 15–20 %.
Рецензенты:
Анненков А.Н., д.т.н., профессор, проректор по научной работе, Воронежский международный институт компьютерных технологий (МИКТ), г. Воронеж;
Климовицкий М.Д., д.т.н., профессор кафедры автоматики и процессов управления, ФГБОУ ВПО «Московский государственный технический университет (МАМИ)», г. Москва.
Работа поступила в редакцию 17.10.2014.