Уровень развития [1] производства торговли (предприятий, объединений, ведомств) зависит от качественного состава выпускаемых изделий. Качественный состав выпускаемых изделий – это такой аспект развития производства, который в числе других факторов обеспечивает выполнение спроса потребителей. Этот аспект описывается различными признаками, которые относятся к отдельному виду товаров, имеющихся в производстве. На основе этого набора признаков сформулируем задачу классификации выпускаемых изделий следующим образом. На каждом месте работы или в быту потребители сталкиваются с выбором качественных предметов из совокупности однородных предметов. Например, при покупке машины, одежды или фруктов мы можем просмотреть вначале целый ряд примерно однородных предметов, прежде чем остановим свой выбор одном из них. Или возьмем другой пример, относящийся к производству: изделия и их качества рассматриваются специальными комиссиями, которые оценивают производственные достижения и качество работы отдельных работников и целых коллективов, затем ранжируются по степеням, качеству работы однородных товаров предприятий и работников. Отсюда видно, что каждый член комиссии выставляет определенную оценку, основываясь на объективных признаках, а также своем профессиональном опыте и интуиции.
Отсюда вытекает вопрос: нельзя ли, анализируя трудовую и качественную деятельность каждого производства товаров, автоматизировать вышеизложенные процессы, используя современные новые информационные технологии? Если этот вопрос реализуется, то не будет нужды создавать комиссии для обработки информации выпускаемых изделий ручным способом, так как у нас будет формализованный способ решения задачи классификации параметров, которые позволяет оценивать качество выпускаемых изделий предприятия.
Классификация выпускаемых изделий на основе удовлетворенности спроса потребителей, т.е. учитывая совокупность качеств в условиях их функционирования, новые информационные технологии предприятий торговли – более сложная проблема. Однако успешное функционирование производства во многом зависит от качественного уровня товаров. Главным критерием распределения выпускаемых товаров по спросам потребителей должен быть только труд – его количество и качество. Однако в практических условиях не всегда бывает так. Возникает различного рода уравниловка, факты начисления зарплаты по существу лишь за явку на работу, а не за ее реальные результаты, выдача незаслуженных премий и т.д. Устранение таких вредных явлений в обществе во многом зависит от формирования социальных качеств работников производства и управляющего персонала предприятий. По этому поводу надо отметить следующие факторы: производство качественных изделий необходимо всегда и повсеместно обеспечивать справедливой и объективной оценкой трудового вклада каждого производящего товар. Надо всемерно поощрять добросовестных работников, не оставлять лодырям и бракоделам никаких лазеек для хорошей жизни при никудышной работе.
Исходя из этого, в настоящее время производство нуждается в подборе таких математических моделей и технологии, которые обладают высокими уровнями качеств выпускаемых изделий.
Постановка задачи классификации качеств выпускаемых изделий на основе их степени спроса и других качественных и количественных признаков осуществляется впервые. Реализацию этой задачи можно использовать как методику руководителями при системе управления и поддержки принятия решений для самоорганизации социально-экономических систем предприятия торговли. Теперь сформулируем постановку задачи на языке математического аппарата.
Пусть L – статистическое пространство. Элементами Fkp ∈ L является множество сырья, подлежащего в производство. Предположим, что каждый из товаров характеризуется набором количественных и качественных признаков Fkp = (f1p, f1p, ..., fnp), которые описывают k-го товара как n-мерные точки в Fkp ∈ L, где p = 1, 2, ..., S – число экспертных оценок, выставляемых для fkp-го признака.
Задача классификации товаров по их качествам производится разбиением L на классы, так что
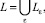
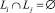
или Li = Lj и отнести Fkp-го товара к одному из классов Lε.
Пространство L является однородным [4], если выполняется условие
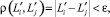
где ε(> 0) –заданное число;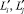 
– выборочное среднее значение соответственно класса Li, Lj(< L) и вычисляется:
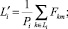
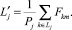
Класс Li является однородным, если выполняется условие
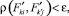(1)
где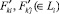 
–выборочные средние значения K и K′ товара вычисляется соответственно:
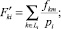
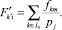
Рассмотрим случайную величину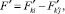 
т.е. разность средних двух выборок F имеет выборочное распределение со средним 
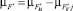и дисперсией
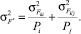(2)
Если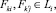 
то обозначая 
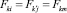и по (2) получаем
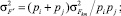(3)
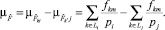(4)
Тогда выборочные оценки дисперсий в классе Li равны
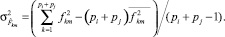(5)
Используя (3) и (5), получим меру рассеяния элементов в пространстве L:
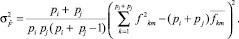(6)
Используя метод максимального правдоподобия [5], определим качества признаков товара в классе Li и Lj:
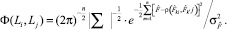(7)
Из (7): 
, учитывая (1), получим
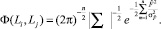(8)
Из (8) вычислим
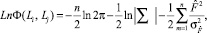
отсюда следует:
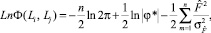(9)
где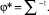 
Из (9) видно, что если
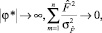
то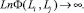 
Функция (7) имеет максимальное значение, если выражение
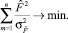(10)
Выражение (10) заменим их значениями, приведенными в (4) и (6):
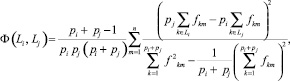(11)
где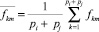 
должна достигаться в минимальном значении при ∀i, j. Однородность класса Li ⊂ L достигается при
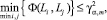(12)
где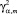 
– пороговое значение, по уровню значимости α и m степенями свободы.
Алгоритм реализации модели (11).
Использование модели (11) при разбиении L на классы Li ⊂ L осуществляется по следующей схеме: во-первых, определяется состав количественных и качественных признаков, описывающих выпускаемые товары. Таким образом, формируются динамические информационные файлы. Во-вторых, должна функционировать информационно-поисковая система «Торговля», которая генерирует необходимые данные для модели (11) в режиме «запрос-ответ». В-третьих, по запросам пользователей формируется матрица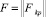 
, где K – число товаров, которые располагается по строкам; p – число признаков, располагается по столбцам. В-четвертых, исходная матрица F разбивается на M матриц:
.
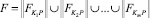В-пятых, для каждой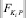 
вычисляется (11) и формируется множество значений
.
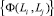На шестом этапе выбирается минимальное значение множества значений:
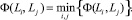
На седьмом проверяется условие (12), если условие выполняется, тогда товары класса Li и Lj объединяются в один класс и процесс продолжается с третьего этапа, иначе вычисление прекращается.
Для апробирования предлагаемой методики на практике рассмотрен следующий пример. С целью принятия обоснованных решений для определения качества выпускаемых продукций необходимо их классифицировать по качественному признаку их использования. Нами выбраны 26 видов товара из предприятий «Шимолгазтаъминот» республики Узбекистан. В этих условиях каждый товар описывается качественными признаками. Сформирована матрица с размерностью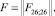 
В случае L = Li = Lj модель (11) использовано для группировки товаров с пороговыми значениями по уровню значимости α = 0,05 и m = 26 степенями свободы. На начальном этапе товары ранжированы по значениям экзогенных признаков. В результате первой итерации получено множество значений Φ(L) на основе модели (11).
Соответственно минимальное и максимальное значение Φ(L) равны:
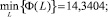
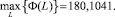
Сравнение этих значений с пороговым указывает, что рассматриваемые группы товаров являются неоднородными, так как условие (12) не выполняется. Во второй итерации товары классифицированы на две группы. В первой группе
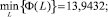
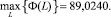
а соответственно, во второй группе
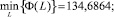
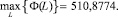
Сравнение порогового значения соответственно по каждой группе показывает, что условие (12) не выполняется. На третьей итерации видно, что условие (12) выполняется.
В результате 26 виды товара классифицированы на четыре группы:
|
Номер класса |
Порядковый номер товара после ранжирования |
|
I |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 |
|
II |
18, 19, 20, 21 |
|
III |
22 |
|
IV |
23, 24, 25, 26 |
В заключение можно сказать, что вышеизложенная модель (2.11) позволяет классифицировать товары по экзогенным признакам, имеющим количественные и качественные значения.
Более предпочтительным (весовым) является класс с номером – I, так как в нем находится 65 % исследуемых товаров. Во втором классе – 15,6 %, в третьем классе – 3,8 % и в четвертом классе – 15,6 % исследуемых товаров.
Это дает возможность оптимального выбора товаров в каждом классе с приоритетом их весомости для формирования запасов качественных выпускаемых изделий.
Рецензенты:
Зольников В.К., д.т.н., профессор, заведующий кафедрой «Вычислительная техника и информационные системы», ВГЛТА, г. Воронеж;
Чевычелов Ю.А., д.т.н., профессор кафедры «Вычислительная техника и информационные системы», ВГЛТА, г. Воронеж.
Работа поступила в редакцию 17.10.2014.