В загрязнение поверхностных и подземных водных объектов фенольными и другими трудноокисляемыми органическими соединениями вносят вклад сточные воды химической, металлургической, горно-перерабатывающей, фармацевтической, целлюлозно-бумажной, пищевой промышленности, фильтрат полигонов твердых бытовых отходов, городские сточные воды.
Фенол является потенциально опасным веществом, вызывающим утомление, головокружение, головную боль, а также снижение иммунитета, оказывает аллергическое и раздражающее действие и способствует развитию злокачественных образований у человека. Фенол нарушает нормальный ход эмбриогенеза, приводя к появлению различных видов уродств у рыб. В результате биохимической деструкции фенола в воде водоемов происходит изменение всех элементов гидрохимического режима.
Актуальной задачей для эффективной очистки жидких промышленных стоков от фенольных соединений является поиск общих закономерностей, свойственных разным схемам трансформации веществ, и построение моделей, адекватно описывающих воздействие физико-химических факторов на уровень снижения органического загрязнителя в водной среде [6].
Современным и высокоэффективным методом удаления органических загрязнителей, содержащихся в промышленных сточных водах, являются процессы, основанные на использовании свободных радикалов в качестве окислителей, получившие название усовершенствованных окислительных процессов (Advanced Oxidation Processes – АОР) [5], достоинством которых является легкость регулирования их скорости в широких пределах с изменением интенсивности светового потока, быстрое и полное их приостановление с прекращением облучения.
Для изучения процессов деградации фенольных соединений в водной среде под воздействием фотохимических факторов и проводились экспериментальные исследования с применением жидкостной и газовой хроматографии, атомной абсорбции, твердо-фазовой экстракции, флуориметрического, экстракционно-фотометрического, иодометрического и титрометрического методов на модельных растворах, содержащих фенольное соединение – бисфенол-А (ВРА). Планирование, проведение и анализ экспериментальных исследований осуществлялись группой исследователей Калужского филиала МГТУ им. Н.Э. Баумана и Тульского государственного университета [6].
Бисфенол А [2,2-(4,4-dihydroxydiphenyl) propane] представляет собой кристаллическое вещество белого цвета, обладает всеми химическими свойствами фенолов, токсичен. Его эмпирическая формула С15Н16О2 (мол. вес 228,29). Предельно-допустимая концентрация в водоемах 0,01 мг/л [1].
При проведении экспериментальных исследований в качестве зависимой переменной выбран показатель «содержание остаточной концентрации ВРА на выходе процесса». На уровень остаточной концентрации фенольного загрязнителя в водной среде в процессе фотодеградации влияют следующие факторы: исходная концентрация ВРА в модельном растворе x1 – CBPA, мг/л; концентрация перекиси водорода x2 – 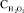 , мг/л; концентрация активатора, содержащего ионы железа (III) x3 – CA, г/л; время облучения x4 – t, ч. Концентрации ВРА измерялись жидкостным хроматографом LC-MS/MS (Agilent 1100 LC совместно с API 2000 LC-MS/MS). Продукты полураспада были определены с помощью газового хроматографа GS-MS (Hewlett Packard 6890 GC совместно с Hewlett Packard 5972A MS).
, мг/л; концентрация активатора, содержащего ионы железа (III) x3 – CA, г/л; время облучения x4 – t, ч. Концентрации ВРА измерялись жидкостным хроматографом LC-MS/MS (Agilent 1100 LC совместно с API 2000 LC-MS/MS). Продукты полураспада были определены с помощью газового хроматографа GS-MS (Hewlett Packard 6890 GC совместно с Hewlett Packard 5972A MS).
При проведении экспериментов был использован фотохимический реактор, включающий ультрафиолетовую лампу (Sankyo Denki, Japan) длиной волны 365 нм.
На основе теории планирования эксперимента [4] построена матрица планирования полного факторного эксперимента (ПФЭ) для исследуемого фотохимического процесса разложения ВРА, приведенная в таблице.
Матрица планирования ПФЭ
|
Опыты |
Планирование |
Зависимая переменная |
||||||||
|
z0 |
кодированный масштаб |
натуральный масштаб |
||||||||
|
z1 |
z2 |
z3 |
z4 |
x1 |
x2 |
x3 |
x4 |
y |
||
|
1 |
+1 |
–1 |
–1 |
–1 |
–1 |
0,05 |
100 |
1 |
1 |
0,036 |
|
2 |
+1 |
+1 |
–1 |
–1 |
–1 |
0,1 |
100 |
1 |
1 |
0,071 |
|
3 |
+1 |
–1 |
+1 |
–1 |
–1 |
0,05 |
200 |
1 |
1 |
0,035 |
|
4 |
+1 |
+1 |
+1 |
–1 |
–1 |
0,1 |
200 |
1 |
1 |
0,068 |
|
5 |
+1 |
–1 |
–1 |
+1 |
–1 |
0,05 |
100 |
2 |
1 |
0,033 |
|
6 |
+1 |
+1 |
–1 |
+1 |
–1 |
0,1 |
100 |
2 |
1 |
0,064 |
|
7 |
+1 |
–1 |
+1 |
+1 |
–1 |
0,05 |
200 |
2 |
1 |
0,031 |
|
8 |
+1 |
+1 |
+1 |
+1 |
–1 |
0,1 |
200 |
2 |
1 |
0,061 |
|
9 |
+1 |
–1 |
–1 |
–1 |
+1 |
0,05 |
100 |
1 |
2 |
0,032 |
|
10 |
+1 |
+1 |
–1 |
–1 |
+1 |
0,1 |
100 |
1 |
2 |
0,062 |
|
11 |
+1 |
–1 |
+1 |
–1 |
+1 |
0,05 |
200 |
1 |
2 |
0,03 |
|
12 |
+1 |
+1 |
+1 |
–1 |
+1 |
0,1 |
200 |
1 |
2 |
0,059 |
|
13 |
+1 |
–1 |
–1 |
+1 |
+1 |
0,05 |
100 |
2 |
2 |
0,028 |
|
14 |
+1 |
+1 |
–1 |
+1 |
+1 |
0,1 |
100 |
2 |
2 |
0,056 |
|
15 |
+1 |
–1 |
+1 |
+1 |
+1 |
0,05 |
200 |
2 |
2 |
0,027 |
|
16 |
+1 |
+1 |
+1 |
+1 |
+1 |
0,1 |
200 |
2 |
2 |
0,053 |
В исследованиях [8] отмечается, что органическое вещество состоит из разных групп соединений, которые имеют разную реакционную способность по отношению к распаду.
Суммарная скорость процесса, описывающая распад всех компонентов, входящих в состав фенольного соединения и продуктов его деградации, зависит от их соотношения в смеси. Если относительное количество стойких компонентов в смеси велико, их распад растянется на более длительное время, чем предсказывает уравнение реакции первого порядка. В водной среде будет оставаться большее количество примесей, что будет понижать допустимый порог загрязнения водного объекта, куда сбрасываются промышленные сточные воды, а при повторяющихся сбросах загрязняющих веществ повысится риск их катастрофического накопления с негативными последствиями для качества воды и жизнедеятельности водной биоты [2].
Анализ исследований [10] позволяет говорить о наличии в многокомпонентном органическом веществе лабильной (легкоразлагаемой) и стойкой (трудноразлагаемой) фракции [2]. При распаде многокомпонентной примеси сначала распадается наиболее лабильная фракция, а затем более стойкая.
Биодеградация органического вещества осуществляется на основе ферментативных реакций, кинетика которых описывается полуэмпирическим уравнением Мозера [2]:
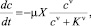 (1)
(1)
где с – концентрация органического вещества; X – биомасса организмов, продуцирующих ферменты; μ – удельная скорость деструкции; K – константа полунасыщения; ν – порядок ферментативной реакции (ν > 0).
В работе [2] показано, что при достаточно низких концентрациях примеси: c << K уравнение (1) можно свести к уравнению
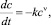 (2)
(2)
(k = μX/Kν – константа скорости реакции), которое в терминах химической кинетики описывает реакцию ν-го порядка.
Нелинейной моделью (2) можно описать процесс разложения фенольных соединений при химическом окислении и фотодеструкции [9].
Решение уравнения (2) при постоянной скорости реакции (реактивности) k имеет вид
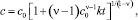 ? ? 1; (3)
? ? 1; (3)
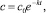 ν = 1, (4)
ν = 1, (4)
где с0 – начальная концентрация примеси.
В зависимости от значения ν возможны три частных случая [2]:
1. При ν < 1
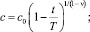
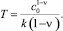 (5)
(5)
Из (5) видно, что распад примеси при ν < 1 завершается за конечное время T.
2. Частный случай ? = 1 соответствует традиционной линейной кинетике dc/dt = –kc и дает экспоненциальный закон распада (4).
3. В случае ν > 1 выражение (3) удобно представить в виде
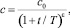 (6)
(6)
где 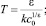
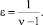
На основе проведенных экспериментальных исследований по влиянию фотохимических факторов на уровень снижения концентрации фенольного загрязнителя ВРА в промышленных сточных водах (таблица) можно идентифицировать экспоненциальную модель снижения концентрации вида (4):
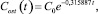 (7)
(7)
где Сost(t) - текущая концентрация фенольного загрязнителя, мг/л; С0 - начальная концентрация фенольного загрязнителя, мг/л; t - время, ч.
Параметр k = ?0,315887 модели (7) получен в системе Statistica нелинейным оцениванием по методу Ливенберга - Марквардта с функцией потерь по наименьшим квадратам. Значение коэффициента множественной корреляции, близкое к единице (R = 0,9408), характеризует, что вариация факторов на 99,9?% объясняет вариацию зависимой переменной. Модель (7) считается значимой на уровне значимости α = 0,01 в связи с тем, что расчетное значение критерия Фишера со степенями свободы f1 = 1, f2 = 15 значительно превышает критическое значение (F = 1258,107 > Fкр(0,99; 1,15) = 8,683117); объясненная доля дисперсии составляет 88,52?%, стандартная ошибка оценки 0,019137. Расчетное значение t-критерия Стьюдента со степенью свободы f2 = 15 превышает критическое на уровне значимости α = 0,01, (t(15) = 16,50662 > tкр(0,99; 15) = 2,60248), что свидетельствует о значимости параметра k = 0,315887, который также принадлежит 99?%-му доверительному интервалу 0,259496 ≤ k ≤ 0,372279 [3].
Кинетику первого порядка следует ожидать в тех случаях, когда рассматривается одна стадия распада индивидуального фенольного соединения, либо когда из нескольких стадий распада только одна является лимитирующей, а остальные проходят быстро.
Для построения управляемой технологии очистки промышленных сточных вод от фенольных соединений на основе использования метода усовершенствованных окислительных процессов необходимо построение математической модели, учитывающей влияние вариаций фотохимических факторов на уровень снижения концентрации фенольного соединения в водной среде.
При построении такой модели необходимо учесть, что в проводимых экспериментах происходит гомогенный фотокаталитический процесс разложения бисфенола-А под действием окислителей: перекиси водорода и хлорида железа (III), активируемый ультрафиолетовым излучением. Исходя из концепции, что скорость процесса разложения ВРА подчиняется закону действующих масс [7], предполагается, что зависимость концентрации фенольного соединения от воздействия фотохимических факторов может быть описана степенной функцией вида [3]:
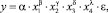
где y - уровень остаточной концентрации BPA в момент времени t, мг/л; x1 - исходная концентрация ВРА в модельном растворе, мг/л; x2 - концентрация перекиси водорода, мг/л; x3 - концентрация хлорида железа (III) (активатора), г/л; x4 - время процесса очистки, ч; α, β, γ, δ, λ - параметры модели; ε - ошибка эксперимента.
В результате анализа, проводимого в Statistica v. 6.1, была получена модель зависимости концентрации фенольного соединения от параметров процесса:
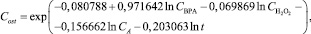 (8)
(8)
где Cost – остаточная концентрация ВРА, мг/л; CBPA – начальная концентрация ВРА, мг/л; 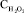 – концентрация перекиси водорода, мг/л; CA – концентрация активатора, содержащего ионы железа (III), г/л; t – время облучения, ч.
– концентрация перекиси водорода, мг/л; CA – концентрация активатора, содержащего ионы железа (III), г/л; t – время облучения, ч.
На основе анализа остатков, полученных в результате множественного линейного регрессионного анализа экспериментальных данных в логарифмическом масштабе факторов, установлено:
1) соблюдение постоянства дисперсии случайных остатков при уровне значимости α = 0,01 на основе критерия ранговой корреляции Спирмена
(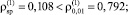
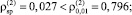
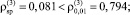
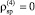 );
); 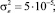
2) независимость случайных остатков (статистика критерия Дарбина – Уотсона – DW = 2,0225). На уровне значимости α = 0,01, при k = 4 и N = 16 нижняя и верхняя процентные точки распределения равны соответственно DWL = 0,53; DWU = 1,66. Исходя из того, что 4 – DW = 1,9775 больше DWU (1,9775 > 1,66), то на уровне значимости α = 0,01 сериальные корреляции остатков ρсер равны нулю;
3) отсутствует корреляционная связь (мультиколлинеарность) между факторами, определитель корреляционной матрицы факторов равен единице (det(rXX) = 1).
Значения коэффициента детерминации, близкого к единице (R2 = 0,9996), а также коэффициента множественной корреляции (R = 0,9998) свидетельствует о достаточно высокой степени связи результата, полученного моделью (8), и факторов, входящих в модель, т.е. вариация факторов на 99,9 % объясняет вариацию остаточной концентрации ВРА.
Модули значений t-критерия Стьюдента, для МНК-оценок параметров модели (8), равные соответственно: t{β1} = 164,732, t{β2} = 11,846, t{β3} = 26,561, t{β4} = 34,427, превышают критическое значение t-критерия t0,99(11) = 2,718, что подтверждает значимость коэффициентов модели на уровне значимости α = 0,01, а свободного члена на уровне значимости α = 0,034 (t{β0} = 2,425 > t0,966(11) = 2,024).
Значимость коэффициента детерминации R2 проверялась с использованием F-критерия Фишера. Гипотеза об одновременном равенстве нулю МНК-оценок параметров регрессии отклоняется, и регрессионная модель (8) считается значимой на уровне значимости α = 0,01, т.к. расчетное значение критерия F превышает его критическое значение (F = 7292,126 > Fкр (0,01; 4,11) = 5,6683) [3].
Принципиальное отличие нелинейной кинетики от линейной заключается в разном поведении при длительном времени. Линейная кинетика дает быстрый экспоненциальный распад, при котором вещество разлагается за некоторое характерное время. Для нелинейной кинетики свойственен более медленный степенной распад, а в случае, когда порядок реакции ν > 2, процесс растягивается на длительное время [2].
Деструкция легкоразлагаемой фракции ВРА в промышленных сточных водах при фотохимическом воздействии подчиняется экспоненциальной модели распада, а трудно разлагаемая фракция может распадаться по степенному закону.
На основе моделирования и статистической обработки экспериментальных данных была идентифицирована значимая экспоненциальная модель распада фенольного соединения, учитывающая синергетические эффекты фотохимического воздействия на уровень снижения фенольного загрязнителя.
Для управления процессом очистки сточных вод на основе оптимального планирования эксперимента построена статистически значимая нелинейная модель, устанавливающая зависимость уровня разложения фенольных соединений в водной среде от параметров фотохимического процесса. Установлено, что нелинейная модель распада органического загрязнителя с высокой степенью точности отражает результаты эксперимента, основанные на законе действующих масс, которому подчиняется скорость процесса фотокаталитического разложения органического субстрата.
Идентифицированные модели фотохимического распада фенольного загрязнителя в водной среде могут быть использованы в задачах мониторинга и управления экологическим состоянием водных объектов при сбросе промышленных фенолсодержащих сточных вод, а также в задачах нормирования антропогенной нагрузки и планирования водоохранных мероприятий.
Рецензенты:
Яшин А.А., д.т.н., д.б.н., профессор кафедры «Общая патология» Медицинского института, ФГБОУ ВПО «Тульский государственный университет», г. Тула;
Короткова А.А., д.б.н., профессор, заведующая кафедрой биоэкологии и туризма ФГБОУ ВПО «Тульский государственный педагогический университет им. Л.Н. Толстого», г. Тула.
Работа поступила в редакцию 23.09.2014.



