Одной из важнейших задач при оптимизации технологического процесса (ТП) производства интегральных схем является формирование математических моделей для каждой технологической операции [7]. Для предлагаемой подсистемы оптимизации [8] необходимы модели, наиболее точно описывающие поведение выходных характеристик изготавливаемой микросхемы.
При формировании таких моделей проблемой является нелинейность зависимости выходного параметра изготавливаемой микросхемы от величины текущего влияния на нее со стороны системы управления ТП. В некоторых случаях невозможно найти аналитическое выражение для описания физического или физико-химического процесса, так как эти процессы зависят одновременно от нескольких факторов, в связи с чем для представления нелинейных функций ТП используются аппроксимации различного вида [3].
Применение численных методов позволяет решить данную задачу: основное их достоинство состоит в том, что большинство из них сводится к многократному повторению простейших арифметических операций для конкретных данных: то есть возможно получить решение для определенного (частного) случая – с учетом особенностей производства интегральных схем. Существующие методы аппроксимации нелинейных функций позволяют получить аналитические зависимости, которые приводят к численным решениям с меньшими временными затратами, при этом выбор метода аппроксимации для конкретной задачи определяется максимальным допустимым временем расчета, погрешностью аппроксимации и прочим [3]. Выбор метода аппроксимации зависит от конкретной задачи, необходимой точности вычислений. Фактически при построении модели необходимо идти на компромисс между точностью модели и сложностью ее вычислений [3].
Необходимо также отметить, что в большинстве случаев для использования в алгоритмах управления технологического процесса работа проводится на ограниченном промежутке (отрезке) функции, в связи с чем для решения задач на производстве требуется аппроксимация только части кривой функций.
Цели работы. По данным работ [1, 4], одними из наиболее важных операций при производстве ИС являются ионная имплантация, отжиг и травление. Исследование и моделирование позволяет разработать алгоритмы контроля и эффективного управления технологического процесса на данных операциях. Целью настоящей работы является исследование существующих математических моделей зависимостей легирующего элемента от глубины залегания в кремнии после ионной имплантации и разработка предложений по их улучшению.
Результаты исследования и их обсуждение
Из теоретических данных [1] известно, что профиль внедренных ионов представляется в виде гауссовой кривой с максимумом концентрации примеси на глубине Rp:
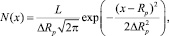
где N(x) – концентрация внедренной примеси; L – доза ионов; Rp – средний пробег ионов, ΔRp – дисперсия среднего проективного пробега.
Однако на практике при имплантации, форма профиля внедренных ионов может существенно отличаться от гауссовой. Причины данного несоответствия теоретических и практических данных связаны, в частности, с тем, что происходит диффузионное перераспределение примеси, наблюдается эффект каналирования, а также влияют другие факторы [4].
В работе [6] показано, что при использовании распределения Гаусса при низких энергиях имплантации ошибка может быть существенной (более 5 %) и ввиду этого не может быть использована в предлагаемой подсистеме оптимизации.
В работах [2, 6] для уменьшения ошибки аппроксимации предлагается использовать Гауссианы более высоких порядков – в частности распределение Пирсон IV [2]:
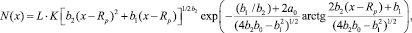
где a0, b0, b1, b2 – константы четырех центральных моментов [2]; K – константа нормализации для распределения.
На рис. 1 представлено сравнение экспериментальных и теоретических данных зависимости концентрации бора от глубины залегания в кремнии после ионной имплантации. Практические данные взяты из работы [6].
Видно, что экспериментальные и теоретические (распределение Пирсон IV) данные имеют достаточно сильные расхождения: несмотря на учет большого числа факторов, что ведет к громоздким формулам и усложнению вычислений вследствие большого числа арифметических операций [2], на некоторых участках зависимости (рис. 1) существует существенное расхождение теоретических и экспериментальных данных (относительная ошибка при значениях x > 1000 нм и энергии 10 кэВ составляет до 11 %), что делает невозможным применение распределения Пирсон IV в подсистеме оптимизации ТП производства интегральных схем для процесса ионной имплантации. Ошибка аппроксимации для распределения Пирсон IV составляет 0,11 для 5 кэВ и 0,25 для 10 кэВ. Согласно работам [2, 6] допустимым считается уровень ошибки аппроксимации не более 1 %.
Следовательно, для применения в подсистеме оптимизации ТП производства ИС производством интегральных схем необходимо использовать более точные для вычисления функции.
В качестве метода аппроксимации предлагается использовать метод наименьших квадратов [5], который состоит в следующем: проводится поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от фактического (экспериментального) была бы наименьшей:
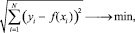
где (x1, y1), (x2, y2), …, (xN, yN) – заданный набор точек (экспериментальные данные).
Аппроксимационная функция ищется в виде многочлена m-й степени:
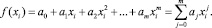
Требуется найти набор коэффициентов аппроксимации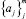 
, для которых значение функции f(xi) будет максимально приближено к практическим данным. Для этого (1) дифференцируется по каждому из параметров aj и приравнивается к нулю. В общем случае получается система уравнений, которая решается в матричном виде.
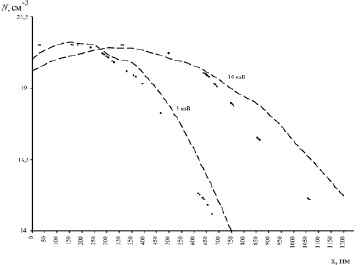
Рис. 1. Зависимости концентрации бора от глубины залегания в кремнии, полученные экспериментально (точки) и теоретически (Пирсон IV) – кривые при дозе 1015 см–2 и энергии 5 и 10 кэВ
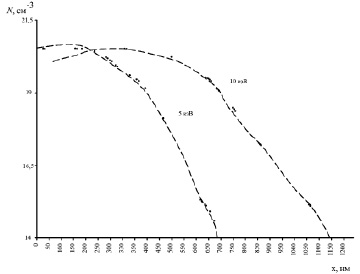
Рис. 2. Результаты аппроксимации экспериментальных данных зависимости концентрации бора от глубины залегания в кремнии при дозе 1015 см–2 методом наименьших квадратов для степени многочлена m = 3
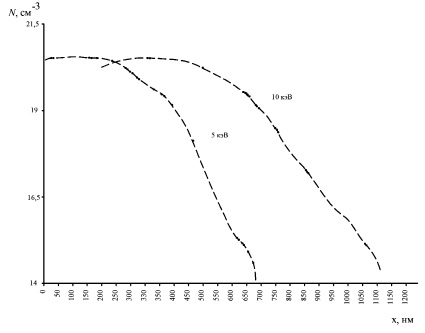
Рис. 3. Результаты аппроксимации экспериментальных данных зависимости концентрации бора от глубины залегания в кремнии при дозе 1015 см–2 методом наименьших квадратов для степени многочлена m = 3
Результаты аппроксимации экспериментальных данных зависимости концентрации бора от глубины залегания в кремнии после ионной имплантации представлены на рис. 2 и 3.
Ошибка аппроксимации составляет для степени многочлена m = 3 – 0,01 для энергии 5 кэВ, 0,017 для 10 кэВ; при m = 4 – 3,2•10–3 для 5 кэВ и 1,45•10–3 для 10 кэВ. При этом требуется выполнить меньше арифметических операций: асимптотическая оценка [5, 6] для метода наименьших квадратов – O(m), для аппроксимации Пирсон IV – O(m2).
Выводы
Таким образом, установлено, что метод наименьших квадратов дает высокую точность аппроксимации для различных значений энергий ионной имплантации бора, является более быстродействующим в сравнении с аппроксимацией Пирсон IV. Для использования в составе разрабатываемой подсистемы оптимизации технологического процесса производства интегральных схем достаточно использовать в методе наименьших квадратов многочлен четвертой степени.
Рецензенты:
Кострова В.Н., д.т.н., профессор, проректор по мониторингу качества, Воронежский институт высоких технологий, г. Воронеж;
Чопоров О.Н., д.т.н., профессор, проректор по научной работе, Воронежский институт высоких технологий, г. Воронеж.
Работа поступила в редакцию 23.09.2014.