В данной работе рассматривается задача построения методами process mining моделей гибких дискретных процессов преобразования ресурсов, структура которых может изменяться как на этапе конфигурирования, так и во время выполнения.
Актуальность данной задачи объясняется следующими положениями:
1) появление моделей гибких процессов обеспечивает дополнительные возможности;
2) иерархическое представление модели гибкого процесса облегчает понимание модели, позволяет использовать в качестве элементов модели существующие формализованные подпроцессы;
3) построение моделей реально выполняющихся процессов обработки ресурсов на основе логов осуществляется методами интеллектуального анализа процессов;
4) существующие методы process mining основаны на использовании аппарата сетей Петри и ориентированы преимущественно на построение моделей дискретных процессов с жестко заданной структурой;
5) перспективным в рамках искусственного интеллекта представляется развитие аппарата алгебры конечных предикатов как средства для идентификации структур для решения задачи построения моделей гибких процессов.
Анализ базовых исследований в данной области
Выполненный анализ базовых исследований в области построения моделей гибких процессов [2, 5, 6, 7, 8] показал, что полная модель такого процесса может быть получена с помощью традиционного полного цикла разработки модели гибкого многовариантного процесса; слияния моделей нескольких «жестких» процессов, которые реализуют идентичную функциональность, но различным способом. Модель строится на основе анализа логов, содержащих информацию о нескольких вариантах реализации процесса [9]. В данной области прослеживается аналогия с ранними стадиями развития технологий программирования, когда основное внимание уделялось алгоритмизации. В дальнейшем произошел переход к объектно-ориентированным технологиям разработки [1].
Предикатная модель гибкого процесса
Использование иерархической модели обеспечивает однозначное определение ситуаций выбора, а также позволяет избежать тупиков. Возможность выбора и отсечения различных вариантов процесса также определяется рассмотренной ранее иерархической структурой предикатов.
Предлагаемый автором метод основан на алгоритме построения блок-структурированного процесса и использует свойство рекурсивности процессного дерева. Как было показано в [3], с каждым узлом данного дерева связано либо конкретное действие процесса, либо один из базовых операторов, задающих взаимосвязи между действиями процесса. Указанные операторы реализованы в виде предикатов АКП.
Действия процесса в предлагаемой модели могут быть описаны как переменной, так и предикатом. Представление действия в виде переменной выполняется для простых действий, которые могут описываться конечным количеством состояний:
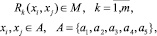(1)
где a1 = «ожидание»; a2 = «готовность»; a3 = «выполнение»; a4 = «приостановка»; a5 = «завершено».
В том случае, если действие процесса является составным и состоит из отдельных элементарных операций, то такое действие представляется в виде соответствующей дополнительной составной переменной предиката. Переменными для такого предиката выступают состояния операций, входящих в состав действия процесса. Например, введем две составные переменные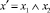 
и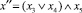 
. Тогда последовательность предикатов
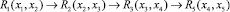
можно заменить на составной предикат
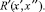(2)
Взаимосвязь действий выполняется с помощью предикатов, реализующих базовые структурные элементы процессной модели, как было показано в [3, 4].
Пусть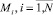 
– N моделей дерева процессов, каждая из которых представлена в виде иерархии предикатов на конечном множестве действий i-го процесса и конечном множестве базовых структурных элементов:
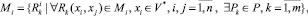(3)
Определим предикат M по правилам АКП, аргументами которого являются модели Mi.
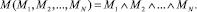(4)
Тогда предикат (4) также является деревом процессов, а входящие в его состав модели можно рассматривать как подпроцессы текущего процесса.
Истинность входящих в состав данного предиката моделей Mi означает выполнимость (достижение его конечного состояния) процесса при допустимых исходных данных.
Следовательно, предикат M будет истинным в том случае, если истинными будут все его аргументы – модели процессов Mi, что и показывает выполнимость интегрального процесса M.
В свою очередь предикат (4) также может быть аргументом у предиката более высокого уровня, что и позволяет рекурсивно определить предикатную модель процесса.
Очевидно, что слияние фрагментов предикатной модели осуществляется путем использования предиката более высокого уровня, аргументами которого являются предикаты, формализующие сливаемые фрагменты:
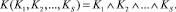(5)
Критерием адекватности полученной модели гибкого процесса является способность воспроизводить все траектории исходных логов, которые были использованы в качестве входных данных при построении модели:
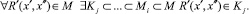(6)
Будем рассматривать две предикатные модели гибкого процесса в качестве изоморфных в том случае, если из обеих могут быть получены идентичные логические сети:
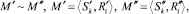(7)
если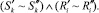 
Метод построения модели гибкого процесса требует предопределенных исходных данных и включает в себя ряд шагов.
В качестве исходных данных выступает лог гибкого процесса L, полученный слиянием k традиционных логов.
Этап 1. При анализе полного лога L выполняется поиск возможностей его разбиения на более мелкие фрагменты Li, которые в дальнейшем могут быть объединены последовательно, параллельно, циклически или через выбор согласно заданным предикатным операциям [4]:
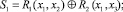
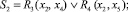
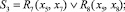(8)
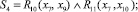
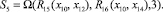
Основные, достаточно очевидные ограничения, которые учитываются при разбиении лога на составляющие:
1. Объединение (обратная к разбиению операция) полученных в результате разбиения логов составляет исходный лог либо является надмножеством для исходного лога L;
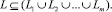(9)
2. Длина Length любого полученного фрагмента Li должна быть не больше длины исходного лога:
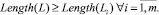(10)
Общий подход к разбиению заключается в выделении последовательностей событий, либо входит в состав более сложных конструкций – выбор, параллельное выполнение, цикл:
(11)
Этап 2. Построение предикатной модели на текущем уровне, когда аргументами предиката являются выделенные на этапе 1 фрагменты. Сами выделенные фрагменты еще не формализованы:
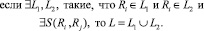(12)
Этап 3. Проверка текущего фрагмента лога: может ли он быть разделен на более мелкие фрагменты:
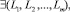(13)
что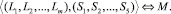 
Этап 4. Если фрагмент лога разделен быть не может, то выбор следующей составляющей модели согласно выражению (10), после чего выполняется переход к этапу 1.
Этап 5. Проверка: все ли доступные фрагменты разделены на составляющие. Если результат положительный, то модель процесса в виде предикатного дерева построена.
Первый базовый элемент отражает отношение непосредственного следования действий процесса. Поэтому работа алгоритма начинается с построения предикатных моделей последовательности операций процесса, каждая из которых объединяет только такие последовательности операций процесса, для которых в логе содержится соответствующая последовательность событий.
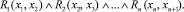(14)
Рассмотрим лог, который представлен в виде следующего набора последовательностей событий («следов» выполнения процесса):
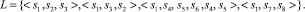(15)
Данный лог отражает следующие возможные элементы процесса:
- ветвление начиная от события s1, поскольку за данным событием в каждом из следов возникают события s2 либо s3, либо s4, либо s7;
- параллельное выполнение действий, которые отражены событиями s2 и s3, поскольку в первой строке событие s2 предшествует событию s3, а во второй – наоборот;
- цикл, поскольку в последней строке пара событий s4, s3 повторяется после события s6;
- последовательности событий s7, s8.
Модель процесса, позволяющая получить рассмотренный выше лог, представляется в виде такого набора предикатов:
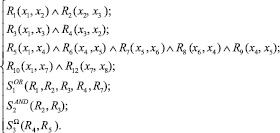(16)
Для нахождения указанной модели целесообразно отдельно выделить ветвление, которое во всех случаях в примере начинается с события s1, а также последовательности событий s2, s3, s3, s2, s4, s5, s3, s6, s4, s5, s7, s8, отражающие параллельное выполнение, простую последовательность и цикл соответственно. Рассматривая каждую из этих групп как единое целое, сворачиваем наш лог к набору простых последовательностей событий, каждое из которых отражается в модели в виде предиката:
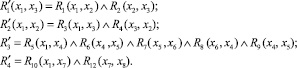(17)
Далее определяется модель для каждой из последовательностей s2, s3, s3, s2, s4, s5, s4, s5, s3, s6, s4, s5, s7, s8. При этом для параллельного выполнения мы разделяем события s2 и s3, для цикла - выделяем отдельно повторяющиеся последовательности s4, s5, а также событие s6, которое предположительно соответствует проверке условия повторения.
Обобщив рассмотренный пример, получаем, что для выделения типовых фрагментов необходимо выполнить следующие основные шаги:
1) разделить лог на последовательности событий, которые не содержат ветвлений;
2) разделить фрагменты лога на последовательности событий, которые не содержат циклов и параллельного выполнения;
3) выделить базовые элементы ветвления, цикла, параллельности между полученными на втором шаге последовательностями событий и представить их в виде предикатов.
Для реализации третьего шага необходимо формализовать признаки, характеризующие наличие в логе ветвления, цикла, параллельного выполнения.
Предварительно доопределим рассмотренные ранее последовательности событий, указав для каждой начальные и конечные события. Тогда для каждой выделенной последовательности событий ∧i существуют начальное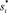 
и конечное события 
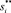так что
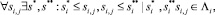(18)
где знак ≤ задает отношение упорядоченности событий во времени (т.е. порядок записи событий в логе).
Теперь определим последовательность, состоящую из произвольного количества событий и отражающую различные версии реализации процесса. Пусть имеем набор упорядоченных последовательностей событий ∧ = {∧i},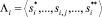 
. Каждая из указанных последовательностей отражает одну из реализаций процесса.
Тогда последовательность действий для процесса выявляется следующим образом. Во-первых, существует выделенный набор последовательностей событий лога ∧ = {∧i}, имеющих идентичные начальные и конечные события. Во-вторых, порядок событий не нарушается в каждой из последовательностей ∧i:
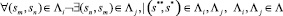(19)
Параллельное выполнение действий процесса является антиподом для последовательности и потому выявляется в том случае, если порядок для пар событий в различных последовательностях из множества ∧ отличается:
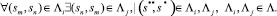(20)
Выбор (ветвление) определим следующим образом. Пусть имеем набор упорядоченных последовательностей событий ∧ = {∧i}, которые имеют общее начальное событие s*. Набор ∧ отражает ветвление в том и только в том случае, если последовательности ∧i не имеют общих событий за исключением начального s*:
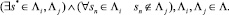(21)
Теперь определим цикл. Последовательность событий ∧i отражает выполнение цикла в модели процесса при выполнении следующих условий:
1) последовательность ∧i не имеет общих событий с другими последовательностями множества ∧:
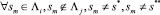; (22)
2) начальное событие текущей последовательности ∧i может иметь последовательную связь с событием из другой последовательности ∧j:
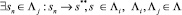; (23)
3) конечное событие текущей последовательности ∧i может иметь последовательную связь с событием из другой последовательности ∧j:
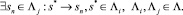(24)
4) существует повторяющаяся не менее 2-х раз последовательность событий, являющаяся подмножеством исходной последовательности ∧i:
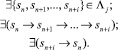(25)
Приведенное в начале параграфа ограничение на полноту лога после описания метода можно задать следующим образом: каждое действие каждого варианта процесса должно быть представлено в логе L = {lk} (т.е. в каждом варианте) хотя бы один раз:
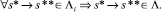(26)
Заключение
В статье предложен рекурсивный метод построения иерархической предикатной модели гибкого процесса на основе анализа логов, который при условии полноты лога обеспечивает построение полного адаптируемого описания процесса в форме иерархии предикатов, связывающих его базовые структурные элементы. Метод обеспечивает возможность проверки адекватности модели в процессе ее построения путем решения системы уравнений, в качестве исходных данных которой выступают логи выполнившегося процесса. Область практического применения предлагаемой модели – интеллектуальный анализ процессов.
Исследование выполнено при поддержке РФФИ в рамках научного проекта № 12-08-00296.
Рецензенты:
Кочегуров В.А., д.т.н., профессор, ФГАОУ ВПО «Национальный исследовательский Томский политехнический университет» Министерства образования и науки РФ, г. Томск;
Кориков А.М., д.т.н., профессор, заведующий кафедрой АСУ факультета систем управления, ФГБОУ ВПО «Томский государственный университет систем управления и радиоэлектроники», г. Томск.
Работа поступила в редакцию 23.09.2014.