Распространённость болезней сердца и огромные социально-экономические потери общества привлекают внимание многочисленных специалистов во всём мире к решению проблемы их ранней диагностики [1]. Среди основных методов диагностики сердечно-сосудистых заболеваний следует выделить метод электрокардиографии (ЭКГ), представляющий собой метод оценки состояния миокарда (сердечной мышцы) и биоэлектрической деятельности сердца путем графической регистрации генерируемых им электрических потенциалов. Электрокардиосигнал содержит информацию как о функциональных возможностях сердца, таких как ритм сердца, частота сердечных сокращений, состояние проводящей системы сердца, кровоснабжение и особенности обменных процессов сердечной мышцы, так и об анатомических отклонениях, связанных с признаками острого или перенесенного инфаркта миокарда, острой или хронической ишемии, гипертрофии предсердий или желудочков, различных видов нарушений ритма сердца и проводимости, нарушения электролитного баланса и других изменения. Благодаря современному развитию компьютерных технологий возможен анализ ЭКГ-сигнала на качественно новом уровне при диагностике кардиологических патологий.
Отображение ЭКГ в фазовом пространстве координат – один из современных методов анализа электрокардиографической информации. Эффективность данного метода обусловлена, прежде всего, тем, что, согласно исследованиям [4, 5, 6, 7], при различных поражениях миокарда изменяется как последовательность пути, так и скорость распространения волны деполяризации и реполяризации по миокарду. Поэтому дифференцированная ЭКГ содержит дополнительную ценную информацию о состоянии сердечно-сосудистой системы испытуемого.
Следует отметить, что хаотические системы легче адаптируются к изменениям условий внешней среды за счет оптимальной перестройки физиологических параметров. Благодаря своей лучшей адаптации при моделировании режимы хаотических изменений в физиологических системах более адекватны среде их существования, чем строго периодические [8]. Нестационарность сигналов ЭКГ делает проблематичным применение широко известных методов Фурье-анализа или Вейвлет-преобразование для анализа электрокардиосигнала [6]. В этих случаях анализ сигнала возможен на основе статистики.
Статистические методы построения фазовой траектории ЭКС
Основная идея метода анализа ЭКГ в фазовом пространстве состоит в построении фазовой траектории электрокардиосигнала в виде графической зависимости между электрокардиосигналом u(t) и ее скоростью изменения во времени, рассчитанной по его производной du(t)/dt. На рис. 1 показан характерный цикл кардиосигнала 1 и увеличенного в 10 раз отношения приращения Δu между двумя соседними измерениями к дискретности изменения времени Δt (кривая 2). Латинскими буквами обозначены элементы кардиоцикла P и T-зубцы и QRS-комплекс.
Фазовая траектория электрокардиосигнала, изображенная в виде кривой 1 на рис. 2, позволяет эффективно выделять QRS-комплекс сигнала и контролировать его свойства [10]. При этом возможность выделения и анализа других зубцов кардиосигнала ограничена из-за наличия внешних влияющих факторов, изменение которых в пределах двух соседних измерений может значительно превосходить изменение полезной составляющей сигнала, что обусловит искажение фазовых траекторий зубцов. Предварительная фильтрация сигнала приводит к его искажению и деформации как формы зубцов, так и их фазовых портретов.
Авторами работы предлагается контролировать скорости изменения сигнала в случае высокой его зашумлённости по значению статистических параметров выборки результатов в окрестности исследуемой точки кривой в текущий момент времени ti. Для этого формируется выборка uj из N значений в i-й момент времени на ограниченном временном интервале N•Δt и находится их математическое ожидание. Отношение удвоенного среднего квадратического отклонения σi значений выборки от их среднего значения к временному интервалу Δt формирования выборки значений определяет касательную функции в i-й модуля скорости для изменения функции сигнала в точке наблюдения значений ЭКС:
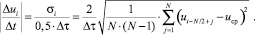(1)
Отличительная особенность фазовой траектории, полученной с применением выражения (1), состоит в том, что значения приращения всегда имеют положительный знак. На рис. 1 модуль фазовой траектории, построенной на основе выражения (1), показан в виде кривой 2, направленной в прямом и обратном направлении.
Для учёта информационного содержания выборки из N значений в окрестности текущего i-го момента времени ti возможен расчёт энтропийного потенциала с помощью выражения вида
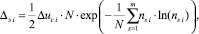(2)
где m – количество интервалов группирования данных (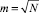
); ns i – количество результатов, попавших в s-й интервал группирования данных для i-го момента времени; Δuг i – ширина интервала группирования результатов.
Учитывая, что энтропийный потенциал пропорционален для заданной выборки среднему квадратическому отклонению, эту величину также можно использовать для оценки модуля скорости изменения электрокардиосигнала в i-й момент времени:
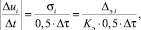(3)
где Kэ – коэффициент энтропии, равный отношению энтропийного потенциала к среднему квадратическому отклонению.
Среди недостатков использования энтропийного потенциала следует отметить его высокую зависимость от информационных свойств выборки данных, что обуславливает сильную зависимость величины от «скачкообразного» воздействия помехи. На рис. 2 и 3 приведены фазовые траектории электрокардиосигнала со «скачкообразным» воздействием помехи.
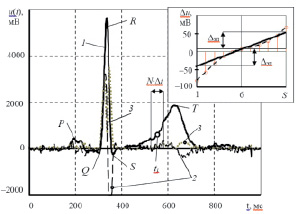
Рис. 1. Кинетические зависимости: 1 – электрокардиоцикла u(t); 2 – увеличенное в 10 раз отношение приращения сигнала Δ u двух соседних значений к дискретности времени Δt; 3 – увеличенного в 3 раза энтропийно-параметрического потенциала Δэп
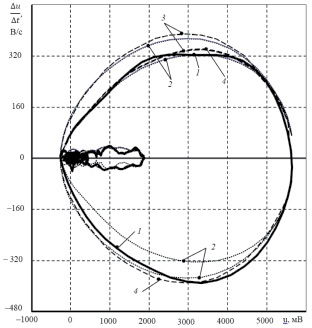
Рис. 2. Фазовые траектории QRS-комплекса: 1 – в пространстве электрокардиосигнала u(t) и его производной du/dt; 2 – в пространстве электрокардиосигнала u(t) и его среднеквадратического отклонения s(t)/Δt; 3 – в пространстве электрокардиосигнала и его энтропийного потенциала Δэ/Δt; 4 – в пространстве электрокардиосигнала u(t) и его энтропийно-параметрического потенциала Δэп/Δτ
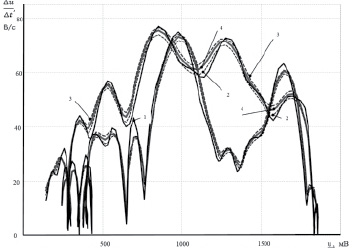а
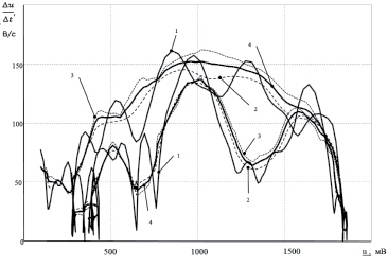б
Рис. 3. а – фазовые траектории T-зубца при количестве значений выборки N, равном 7 (номера кривых соответствуют рис. 2); б – фазовые траектории T-зубца при N, равном 13 (номера кривых соответствуют рис. 2)
Учесть информационные свойства выборки результатов в i-й момент времени ti при условии сохранения гладкости функции и снижении влияния «скачкообразной помехи» позволяет использование энтропийно-параметрического потенциала вида
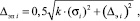(4)
где k – коэффициент сглаживания, позволяющий обеспечить сохранность состояния системы при «скачкообразных воздействиях», соответствующих низкой энтропии информации в выборке. Значения коэффициента k выбираются в интервале от 1 до 3.
Тогда для оценки модуля скорости изменения электрокардиосигнала в i-й момент времени, построенной на основе энтропийно-параметрического потенциала, справедливо выражение
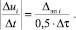(5)
Модуль фазовых траекторий, построенных с учётом выражения (5) для энтропийно-параметрического потенциала, показан на рис. 2 в виде пунктирной линии 3.
Для построения фазовой траектории, приближенной к классической форме, необходимо учесть направление изменения величины, что достигается с помощью умножения модуля величины на функцию знака:
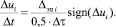(6)
Обозначим Gi, знак приращения значений электрокардиосигнала в два соседних момента времени, Gi = sign(Δui), записав на основе булевых соотношений вида
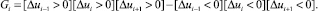
Фазовая траектория, построенная с учётом изменения знака, показана на рис. 2 в виде кривой 4. На основе рис. 2 можно видеть хорошее совпадение фазовых траекторий, построенных на основе дискретных приращений 1 и на основе энтропийно-параметрического потенциала 4.
Достоинства статистических методов контроля электрокардиосигнала проявляются при анализе T-зубца, для которого классическая фазовая траектория, построенная в пространстве электрокардиосигнала и его первой производной, дана на рис. 3. Из рассмотрения фазовых траекторий электрокардиосигнала T-зубцу следует отметить следующее: амплитуда колебаний фазовых траекторий, построенных с применением предлагаемых параметров (кривые 2, 3, 4), значительно меньше построенной на основе дискретных приращений 1. Таким образом, фазовые траектории, построенные с помощью статистических методов, обладают свойством стабильности, что проявляется в уменьшении влияния высокочастотного воздействия помехи. Свойство стабильности проявляется в приближении статистической кривой к аттрактору кардиосигнала и сохранении формы фазовой траектории, которое усиливается при увеличении количества значений в выборке N группирования данных. На рис. 3, б, дан пример повышения стабильности фазовой траектории при увеличении N, где кривая 4 является фазовой траекторией, построенной с применением энтропийно-параметрического потенциала. Данная кривая сохраняет особенности контроля скорости изменения ЭКС, характерные как для среднеквадратического отклонения, так и энтропийного потенциала, что следует непосредственно из выражения (4), где в энтропийно-параметрический потенциал заложено отражение обоих параметров.
Таким образом, оценка приращения скорости изменения электрокардиосигнала в i-й момент времени с помощью энтропийно-параметрического потенциала, рассчитанная по выборке значений, более устойчива к влиянию внешних воздействий в сравнении с использованием классических приращений Δu и позволяет более надежно выделить QRS-комплекс и T-зубец электрокардиосигнала.
Рецензенты:
Трофимов А.А., д.т.н., доцент, зам. начальника учебно-научного центра ОАО «НИИФИ», г. Пенза;
Чувыкин Б.В., д.т.н., профессор кафедры ИВС, ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.
Работа поступила в редакцию 23.09.2014.