В 1936 году бельгийский инженер T.И.C. Вермейрен обнаружил, что при нагревании воды, пересекшей силовые линии магнитного поля, на теплообменной поверхности не образуется накипь (отложение, инкрустация). Первый в мире патент на аппарат магнитной обработки воды был выдан T.И.C. Вермейрену 01.10.1946 г.
С тех пор началось активное применение магнитных полей для обработки жидкостей, главным образом в теплоэнергетике, где каждый миллиметр осадка на стенке нагревательного котла снижает мощность нагрева на 5 %. В общемировых масштабах годовой ущерб составляет многие миллиарды долларов. Однако долгое время наука не могла понять причины проявления этого эффекта, поскольку вода, как считалось, не обладает магнитными свойствами. Из-за отсутствия на сегодняшний день удовлетворительной теории количественно предсказывать результаты магнитной обработки воды (МОВ) затруднительно. В данной работе представлена гипотеза, поясняющая механизм снижения накипи и позволяющая делать адекватные количественные оценки противонакипного эффекта при омагничивании водного потока.
Широко известно объяснение противонакипного эффекта МОВ на основе теории ДЛФО (Дерягин, Ландау, Фервей, Овербек) [5], согласно которой сила Лоренца деформирует двойной электрический слой (ДЭС) коллоидной частицы (КЧ), вызывая коагуляцию коллоидного раствора [1].
На рис. 1 показана положительно заряженная коллоидная частица CaCO3, находящаяся в водной среде. Ее заряд создают так называемые потенциалообразующие или ко-ионы Ca2+, CaCO3, которые химически закреплены на поверхности частицы. Вокруг коллоидной частицы расположен очень тонкий слой Штерна (порядка 1–2 атомных размеров), содержащий кроме потенциалообразующих ионов также захваченные отрицательные противоионы 
. Дальше в водном растворе, окружающем коллоидную частицу, расположен диффузионный слой, состоящий преимущественно из анионов бикарбоната кальция 
.
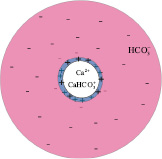
Рис. 1. Строение двойного электрического слоя коллоидной частицы CaCO3
Согласно теории ДЛФО взаимодействие двух заряженных частиц обусловлено как силами молекулярного притяжения, так и силами электрического отталкивания. Суперпозиция этих сил для энергии взаимодействия дает формулу
E = E1 + E2, (1)
где лондоновская энергия притяжения определяется формулой Гамакера:
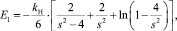(2)
а выражение для кулоновской энергии отталкивания следующее:
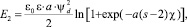(3)
где ψd – электростатический потенциал на границе штерновского и диффузионного слоев, который почти во всех теоретических работах приравнивается к электрокинетическому потенциалу коллоидной частицы; kH – константа Гамакера; ε0 – электрическая константа; ε – диэлектрическая постоянная для воды;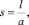 
где l – расстояние между центрами частиц эффективного радиуса a; 
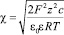– обратная длина Дебая; F – число Фарадея; R – универсальная газовая постоянная; T – абсолютная температура; z – степень ионизации ионов; c – мольная концентрация ко-ионов вдали от коллоидной частицы.
Для эксперимента, описанного в [9], имеем: T = 300 K, C = 2,6 моль/м3, z = 2, длина Дебая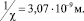 
Из-за высокого потенциального барьера электрического отталкивания коагуляция обычно не происходит и коллоидный раствор стабилен [4]. Согласно [5] вероятность коагуляции определяется безразмерной величиной 1/W, где W – так называемый коэффициент замедления
(4)
В стабильном коллоидном растворе W >> 1.
Расчеты, проведенные по формулам (1)–(4) в условиях эксперимента [9] (B = 0,2 Т, τ0 = 0,25 с, v = 2 м/c), показали [3, 4], что после магнитной обработки начинается интенсивная коагуляция и раствор теряет устойчивость. Частицы укрупняются, раствор для них становится пересыщенным и поток кристаллизации молекул солей жесткости перераспределяется от стенок трубы к взвеси. Таким образом, МОВ за счет деформации двойного электрического слоя коллоидных частиц вызывает коагуляцию. Это первый фактор, запускающий комплексный механизм МОВ.
Для дальнейшего анализа полезно подробнее рассмотреть поведение зародыша CaCO3 радиуса r в пересыщенном растворе. По отношению к критическому зародышу (r = rcr) раствор не имеет пересыщения, и такой зародыш с равной вероятностью может сорбировать на своей поверхности молекулу из раствора либо десорбировать молекулу со своей поверхности. После сорбции зародыш становится закритическим (r > rcr), далее монотонно растет и переходит в осадок. После десорбции зародыш становится докритическим (r < rcr) и снова исчезает. Итак, наиболее устойчивая форма твердой фазы в растворе – критические зародыши, но гетерогенной кристаллизации из раствора, по определению, на них не происходит.
Итак, важно отметить, что с началом коагуляции в результате магнитной обработки водный поток приобретает новое качество – в нем возникает твердая фаза надкритического размера. Ее поверхность начинает конкурировать с поверхностью теплообменника в процессе выпадения солей накипи из пересыщенного раствора. Понятно, чем больше площадь поверхности взвеси, тем большая часть общей массы накипи оседает на ней и, соответственно, меньше накипи оседает на стенке теплообменника. Это второй фактор, участвующий в механизме противонакипного эффекта МОВ.
Величина критического радиуса rcr0, согласно уравнению Гиббса – Томсона [5], определяется выражением
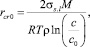(5)
где с0 = 0,14 моль/м3 – равновесная мольная концентрация кальцита в воде; М = 0,1 кг/моль – молярная масса CaCO3; ρ = 2711 кг/м3 – плотность твердой фазы; σs.l – поверхностное натяжение на плоской границе твердая фаза/жидкость.
Краевой угол смачивания плоской границы раздела твердая фаза (кальцит) – жидкость (вода) равен J = 20°, тогда легко показать, что σs.l = 0,16 Дж/м2 [3]. Однако, как показано в [7], при гомогенной генерации зародышей малого радиуса проявляется размерный эффект – при наличии протяженной межфазной области, соизмеримой с радиусом наночастицы, заметное влияние оказывает толщина поверхностного слоя, характеризуемая константой Толмена d. При этом процесс гомогенного формирования наноразмерного зародыша определяется эффективным значением seff, которое зависит от d и существенно снижается, облегчая рождение новых зародышей в пересыщенном растворе. Радиус реального критического зародыша вычисляется по формуле
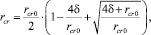
где параметр δ принимает значения в интервале 0 ≤ δ ≤ 1,5rcr0 (rcr0 – значение радиуса критического зародыша, соответствующее (5)). Зависимость радиуса критического зародыша rcr от безразмерного параметра Толмена δ/rcr0 дана на рис. 2.
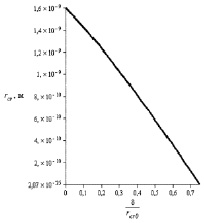
Рис. 2. Зависимость радиуса критического зародыша rcr от нормированного параметра Толмена d/rcr0
Зависимость поверхностного натяжения seff от радиуса критического зародыша rcr с учетом размерного эффекта аппроксимирована формулой Толмена [7]:
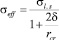
и показана на рис. 3. Энергия Гиббса образования зародыша с радиусом r [6]:
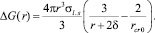
Будем считать, что в водном растворе соли CaCO3 присутствуют лишь зародыши с размером, близким к критическому: большие зародыши отсутствуют ввиду малой вероятности их образования, а маленькие исчезают сразу после появления. Если разложить функцию ΔG(r) по малому параметру (r – rcr), сохраняя только квадратичные члены, и учесть, что первая производная по определению в точке максимума равна нулю, можно написать
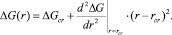
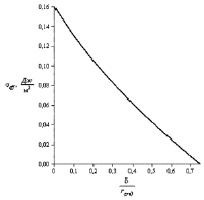
Рис. 3. Зависимость эффективного поверхностного натяжения seff от нормированной константы Толмена d/rcr0
Тогда для функции распределения зародышей с размерами, близкими к критическому, получим выражение
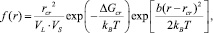
где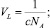 
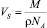– объемы, приходящиеся на одну молекулу CaCO3 в воде и зародыше; N – число молекул в критическом зародыше. Величина b определяется по формуле
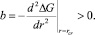
Радиус критического зародыша лежит в критической области, где значение свободной энергии Гиббса лежит в диапазоне, определяемом величиной тепловой флуктуации kBT:
,
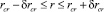где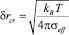 
.
Тогда концентрация критических зародышей определяется интегралом
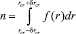, (6)
график которого приводится на рис. 4.
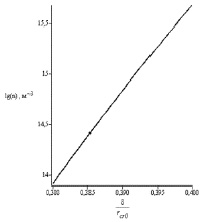
Рис. 4. Зависимость концентрации критических зародышей (в логарифмическом масштабе) от нормированной константы Толмена d/rcr0
Как и ожидалось, влияние размерного эффекта уменьшает величину поверхностного натяжения и радиус критических зародышей, увеличивая их концентрацию в растворе. Соответственно, ускоряется процесс кристаллизации солей накипи на взвесь, чем усиливается эффект МОВ. Таким образом, размерный эффект вносит существенный вклад в уменьшении накипи при МОВ. Это третий фактор, участвующий в механизме противонакипного эффекта МОВ.
При отсутствии магнитного поля весь поток I10 (моль/с) молекул CaCO3 осаждается на стенки теплообменной трубы в соответствии с формулой
I10 = β1Lπd(C – C0),
где πLd – площадь поверхности трубы диаметра d и длины L.
Коэффициент массопередачи β1 на поверхность стенки теплообменника (м/с) зависит от гидродинамических характеристик потока в канале и для турбулентного потока в круглой трубе описывается выражением [6]:
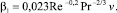
Здесь Re и Pr – числа Рейнольдса и Прандтля, а v – скорость водного потока в трубе.
После магнитной обработки тот же самый поток молекул распределяется между взвесью и стенкой пропорционально их площадям и коэффициентам массопередачи, причем размер частиц взвеси и пересыщение раствора по отношению к этим частицам изменяется в ходе коагуляции, и на каждом k-м ее этапе определяется теорией быстрой коагуляции Смолуховского [5]. С учетом этого поток молекул I2mag (моль/с) на поверхность кристаллов, взвешенных в водном потоке, вычисляется по формуле
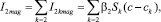(7)
где β2 – коэффициент массопередачи между жидкостью и зародышем радиуса r. Следует отметить, что коэффициент массопередачи солей накипи на поверхность взвеси рассчитывается иначе, чем на стенки теплообменника. Процесс осаждения накипи на взвесь не связан с гидродинамикой, поскольку частицы взвеси переносятся вместе с потоком жидкости, поэтому массообмен протекает за счет молекулярной диффузии и эквивалентен массопереносу на твердую сферу в неподвижной среде. В соответствии с [8]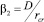 
(D – коэффициент диффузии молекул СаСО3 в воде). Как отмечалось ранее, процесс осаждения накипи на стенках трубы в сильной мере зависит от гидродинамики течения, тогда как кристаллизация на взвеси определяется молекулярной диффузией. Различие физической сущности процессов массопереноса СаСО3 на взвесь и на стенки приводит к существенному отличию соответствующих коэффициентов β2/β1 = 7•104 в условиях эксперимента [9], что вносит существенный вклад в снижение накипи при МОВ. Это четвертый фактор, участвующий в механизме противонакипного эффекта МОВ.
В (7) I2kmag, Sk и Ck соответственно поток молекул накипеобразователя на частицы k-го порядка коагуляции, или порядка k, общая поверхность таких частиц и равновесная мольная концентрация молекул СаСО3 относительно частицы порядка k.
Суммирование в (7) распространяется на все частицы, кроме первичных с k = 1 (критического радиуса), так как для них по определению пересыщение отсутствует и поток кристаллообразующих молекул на них равен нулю (процессы сорбции и десорбции уравновешены).
Поскольку частица k-го порядка имеет радиус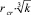 
, то для нее справедливо соотношение [3]:
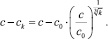
Тогда поток кристаллизации молекул CaCO3 на поверхность коллоидной частицы k-го (k = 2, 3, …) порядка в омагниченном водном потоке определяется выражением
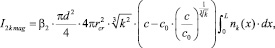(8)
где nk(x) – концентрация коллоидных частиц порядка k на расстоянии x от начала трубы.
Критические зародыши с начальной концентрацией n (6) коагулируют, образуя частицы надкритического размера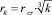 
на k-м этапе коагуляции. По отношению к ним увеличивается пересыщение (с – сk) раствора и поток молекул CaCO3 на частицу k-го порядка постепенно возрастает. В формуле (8) за время t расстояние от начала трубы определяется по формуле x = vt.
Теория быстрой коагуляции Смолуховского дает следующее выражение для расчета изменения со временем концентрации nk(t) коллоидных частиц первого, второго и др. порядков [5]:
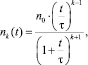k = 1, 2, 3, ... (9)
где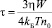 
так называемое время коагуляции, причем коэффициент замедления W определяется выражением (4); η – динамическая вязкость воды при температуре T.
Формула (9) в нашем случае требует уточнения, т.к. она не учитывает того, что уменьшение концентрации критических зародышей в ходе коагуляции неизбежно должно сопровождаться восполнением их концентрации до равновесной за счет гомогенной нуклеации новых частиц в объеме пересыщенного раствора. Появление новых зародышей увеличивает поверхность взвеси и также вносит вклад в противонакипный эффект. Это пятый фактор, участвующий в механизме противонакипного эффекта МОВ.
Уточненная формула для расчета концентрации коллоидных частиц nk(t) (k = 2, 3, ...) со временем учитывает восполнение концентрации первичных (критических) зародышей и имеет следующий вид [3]:
n1(t) = n0 = const,
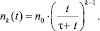(10)
Подстановкой (10) в (8) с учетом x = vt находится поток молекул CaCO3 на коллоидные частицы I2kmag.
Проведем количественный расчет антинакипной эффективности МОВ. Противонакипный эффект – снижение накипи на стенках трубы (теплообменника) за счет магнитной обработки воды – определяется удобной для практики формулой
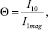
где I10, I1mag – поток молекул СаСО3 на стенке теплообменника при отсутствии и наличии МОВ соответственно. В работе [2] показано, что при таком механизме магнитной обработки справедлива формула:
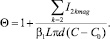(11)
Из формулы (11) с учетом (8) видно, что противонакипный эффект МОВ кроме отношения коэффициентов массопереноса на взвесь и на стенки зависит также от соотношения площадей поверхности взвешенных частиц и стенок. Из вышеизложенного ясно, что после начала коагуляции это соотношение стало резко увеличиваться в пользу поверхности взвеси. Это шестой фактор, участвующий в механизме противонакипного эффекта МОВ.
Переходя к количественным оценкам, вычислим по (11) зависимость коэффициента Q от безразмерной константы Толмена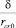 
, которая представлена на рис. 5. С помощью данного графика, зная величину Θ= 30 из эксперимента [9], можно оценить d ≈ 0,4 нм, что согласуется с ожидаемым значением данного параметра δ < 1 нм [7] и является косвенным доказательством адекватности представленной модели. Кроме того, rc ≈ 0,83 нм, число молекул в критическом зародыше N ≈ 40 и σeff ≈ 0,064 Дж/м2.
Резюмируем изложенную выше гипотезу о механизме снижения накипи при магнитной обработке водного потока. В основе гипотезы – положения известной теории ДЛФО о деформации двойного электрического слоя силами Лоренца в магнитном поле с утратой устойчивости коллоидного раствора и коагуляцией коллоидных частиц. Показано, что шесть существенных обстоятельств определяют величину противонакипного эффекта:
1. Деформация двойного электрического слоя дает начало процессу коагуляции коллоидных частиц.
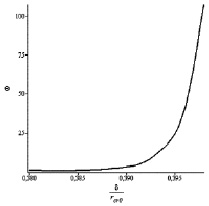
Риc. 5. Зависимость коэффициента Θ от нормированного параметра Толмена d/rcr0
2. По отношению к коагулированным частицам на начальных этапах коагуляции пересыщение раствора резко возрастает и в объеме воды идет активная кристаллизация на поверхность взвеси.
3. Влияние межфазного слоя, определяемого константой Толмена, уменьшает энергию образования критических зародышей, экспоненциально увеличивая скорость их гомогенной генерации и концентрацию в растворе.
4. Массоперенос кристаллизующихся молекул из водного раствора на взвесь протекает намного активнее, чем на стенки теплообменника.
5. Убыль концентрации критических зародышей непрерывно восполняется за счет гомогенной генерации новых критических зародышей для сохранения динамического равновесия жидкой и твердой фаз в пересыщенном растворе.
6. Увеличение концентрации взвеси в объеме омагниченного водного потока приводит к радикальному перераспределению накипи между стенкой и взвесью в пользу последней, что и определяет наблюдаемый противонакипный эффект магнитной обработки.Таким образом, определена совокупность известных физических явлений, приводящая к противонакипному эффекту, отмеченному в эксперименте [9], причем значение константы Толмена, при которой реализуется указанный эффект, согласуется с известной оценкой диапазона ее значений. Это в целом подтверждает предложенную авторами гипотезу о механизме снижения накипи при магнитной обработке воды.
Рецензенты:
Яновский Ю.Г., д.т.н., профессор, директор, ФГБУН «Институт прикладной механики» Российской академии наук, г. Москва;
Бошенятов Б.В., д.т.н., ведущий научный сотрудник, ФГБУН «Институт прикладной механики» Российской академии наук, г. Москва.
Работа поступила в редакцию 15.09.2014.