Scientific journal
Fundamental research
ISSN 1812-7339
"Перечень" ВАК
ИФ РИНЦ = 1,674

Personal portfolio

THEORETICAL AND EXPERIMENTAL STUDIES OF MOMENT OF EXTERNAL FORCES ON ROTARY EXPANSION OF PIPE

Hein Win Zaw 1
1 «MATI» – Moscow State Aviation Technological University Russian University of Technology
Processes of local deformation (rotary extractor, reeling, rotary sealer, etc.) when compared to traditional metal forming operations have a number of advantages: less deforming force, simple tooling, high degree of forming the preform. Much work on the complexity of the technological production preparation stage in the aircraft is connected to a certain extent so that the manufacture of parts possible plastic deformation of the original billet is always limited, both theoretically and in practice are important processing methods that increase the limit of deformation of the workpiece. This leads to a reduction in processing steps and transitions, which ultimately reduces the complexity of manufacturing details. Therefore, research in the field of local deformation are relevant.During rotary expansion, a tubular element preform was placed between two rollers, under the action of forces which deform the wall of the preform P by increasing its diameter. Unrolling known pieces, when instead of a rotating roller outer ring or matrix. In the latter case the initial preform initially has a smaller diameter and is rolled to the inside diameter of the ring (matrix), which improves the accuracy of manufacturing the part. Rolling processes are implemented in terms of external compression procurement elements in the deformation zone, but in the inner layers of the workpiece may occur and tensile stresses. From the theory of rolling known that the tensile stress in the medial layers of the preform may reach considerable values, such schemes are therefore important and modes of processing that would have led to a reduction of the tensile stress.
results of calculation and experiment for the required torque M
1. Popov E.A., Kovalev V.G., Shubin I.N. Technology and automation stamping. – Moscow: Publishing House of the MSTU. NE Bauman, 2003. 480 р.
2. Stamping. Calculation of process parameters. Directory / V.I. Ershov, O.V. Popov, A.S. Chumadin etc. M.: Publishing house MAI, 1999. 516 р.
3. LM Kachanov Fundamentals of the theory of plasticity. Moscow: Nauka, 1996. 420 р.
4. Chumadin A.S., Burstein N.M., Arhipov V.N., Way of change of diameter of a trailer site of a pipe. no. 2104112, 1998 patent Russian Federation.
5. Abibov A.L., unsociable persons of H.M., Fighters of B.B., etc. Technology of aircraft construction. M.: Mechanical engineering, 1970. 499 p.
6. Sheet stamping. Calculation of technological parameters. Directory / Century. I.Ershov, O.V. Popov, A.S. Chumadin, etc. M.: MAI publishing house, 1999. 516 p.
7. Hein Win Zaw Experimental studies of the process rolling tubes // Forging and stamping production. Materials processing pressure. Number 12, 2007, pр. 11–14.

Процессы локального деформирования (ротационная вытяжка, раскатка, ротационный обжим и другие) по сравнению с традиционными операциями обработки металлов давлением обладают рядом достоинств: меньшее деформирующее усилие, простота технологической оснастки, большие степени формоизменения заготовки.

Большая трудоемкость работ на этапе технологической подготовки производства в самолетостроении связана в известной мере с тем, что при изготовлении деталей возможности пластического деформирования исходной заготовки всегда ограничены, поэтому и в теоретическом, и в практическом плане важное значение имеют методы обработки, которые увеличивают предельные деформации заготовки. Это ведет к уменьшению технологических операций и переходов, что в конечном итоге снижает трудоемкость изготовления деталей. Поэтому исследования в области локального деформирования являются актуальными.

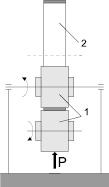
При раскатке (рис. 1, а) элемент трубчатой заготовки помещают между двумя роликами, которые под действием усилия Р деформируют стенку заготовки, увеличивая ее диаметр. Известна раскатка заготовок, когда взамен наружного ролика используется вращающее кольцо, или матрица (рис. 1, б) [1, 2]. В последнем случае исходная заготовка имеет первоначально меньший диаметр и раскатывается до внутреннего диаметра кольца (матрицы), что повышает точность изготовления детали.

Процессы раскатки реализуются в условиях внешнего сжатия элементов заготовки в очаге деформации, однако во внутренних слоях заготовки могут возникать и растягивающие напряжения. Из теории прокатки известно, что растягивающие напряжения в срединных слоях заготовки могут достигать значительной величины, поэтому важны такие схемы и режимы обработки, которые бы приводили к снижению этих растягивающих напряжений.

Рассмотрим симметричный процесс раскатки с двумя ведущими оправками одинакового диаметра (рис. 2). Разобьем заготовку на две равные части и в силу симметрии рассмотрим только одну (верхнюю) часть.

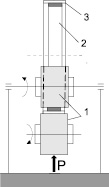pic_66.wmf аpic_67.wmf б

Рис. 1. Схема раскатки кольцевых заготовок: а – между двумя роликами; б – между кольцом и роликом (1 – ролики; 2 – заготовка; 3 – кольцо (матрица))

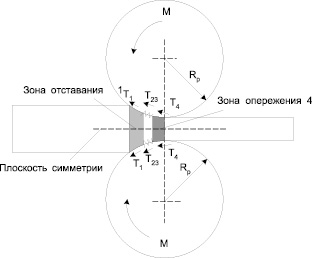
pic_68.wmf

Рис. 2. К определению крутящих моментов двух ведущих оправок

Деформирование осуществляется за счет вращения оправки. Момент внешних сил М, прикладываемый к ведущей оправке, создает в зонах прилипания 2 и 3 активную силу Т23, которая обеспечивает перемещение заготовки и работу деформации, а также силы пассивного трения в зоне отставания Т1 и в зоне опережения Т4, работы которых увеличивают величину внешнего момента М.

Относительно оси вращения верхней ведущей оправки равенство моментов указанных сил имеет вид

М = (Т23 + Т1 + Т4) Rp. (1)

Для двух ведущих оправок будем иметь

2М = 2(Т23 + Т1 + Т4) Rp,

где 2Т23 Rp – внешний момент, который обеспечивает работу деформации Адеф, т.е.

2 Т23 Rp = Адеф/φ,

где φ – угол поворота оправки за один оборот заготовки.

Таким образом, выражение (1) для двух ведущих оправок может быть переписано в виде

2М = Адеф/φ + 2(Т1 + Т4) Rp . (2)

В уравнении (1) силы трения в зоне отставания Т1 и в зоне опережения Т4 равны:

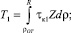
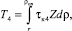heyn01.wmf heyn02.wmf (3)

где τк1, τк4 – контактные касательные напряжения от действия сил контактного трения, рассчитываемые выражениями (1), (2) соответственно; Z – единичная ширина очага деформации (Z = 1); ρ – текущий радиус.

Аналитически расчет уравнений (3) с некоторой погрешностью может быть осуществлен через средние подынтегральные значения τк1, τк4, зная размеры контактных зон.

Рассмотрим процесс раскатки с двумя оправками разного диаметра, одна из которых (верхняя) – ведущая, а вторая (нижняя) – ведомая (рис. 3).

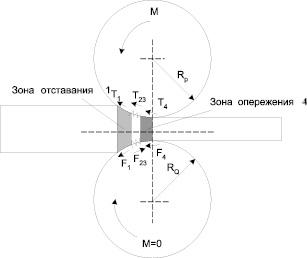
pic_69.wmf

Рис. 3. К определению крутящих моментов при одной ведущей оправке

Относительно оси вращения верхней ведущей оправки равенство моментов будет иметь вид (1), где Т23Rp – момент активной силы, необходимый для формообразования заготовки и вращения ведомой оправки, т.е.

Т23Rp = Адеф/φ + F23RР.

На ведомую (нижнюю) оправку со стороны заготовки действует активная сила F23 и силы пассивного трения F1 и F4, моменты которых уравновешиваются, т.е.

F23RQ = (F1 + F4) RQ (4)

или

F23 = (F1 + F4). (5)

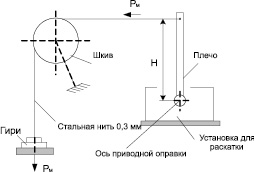
pic_70.wmf

Рис. 4. Схема приспособления для определения крутящего момента

Таким образом, уравнение моментов для одной ведущей оправки (рис. 3) будет иметь вид

М = Адеф/φ + F23RР + (Т1 + Т4) Rp (6)

или

М = Адеф/φ + (Т1 + Т4 + F1 + F4) Rp. (7)

Момент внешних сил (крутящий момент) определялся с использованием специального приспособления, установленного на установке для раскатки, схема которого приведена на рис. 4, а внешний вид представлен на рис. 5.

Величина момента (рис. 4) определялась по известной формуле М = Рм Н в момент перемещения заготовки под заданной нагрузкой. Влияние сил трения в передачах установки (шкив, редуктор и т.д.) компенсировалось специальной установочной гирей.

Результаты экспериментов применительно к ведущей давильной оправке Ø 24 мм и ведомой – Ø 60 мм приведены в табл. 1.

pic_71.tif

Рис. 5. Общий вид приспособления для определения крутящего момента

Таблица 1

Момент внешних сил при раскатке

№ п/п

Заготовка, материал, размеры

Усилие со стороны давильной оправки, кг

Вес гирь Рм, кг

Плечо Н, м

Толщина в зоне контакта, мм

Момент, М, кгм

1

Полоса, АМг6М

20×1,95 мм

500

3,85

0,34

1,93

1,29

2

750

3,45

0,34

1,90

1,17

3

1000

6,0

0,34

1,80

2,04

4

Труба

Д16Т

Ø 30×10×1,5

500

3,2

0,34

1,45

1,09

5

1000

4,5

0,34

1,40

1,53

6

Полоса

Д16Т

20×0,95 мм

1000

4,4

0,34

0,93

1,50

7

1500

6,4

0,34

0,90

2,18

8

Труба

АМг6М

Ø 50×24×2,1

1000

4,8

0,34

2,05

1,63

9

1500

6,5

0,34

1,95

2,21

В табл. 2 приведено сопоставление результатов расчета и эксперимента по необходимому крутящему моменту М для деформирования плоских и трубных заготовок.

Таблица 2

Результаты расчета и эксперимента по необходимому крутящему моменту М

№ п/п

Заготовка, материал, размеры

Погонное усилие, Р/L, кг/мм

Длина очага, а = b, мм (экспер)

Длина очага, а = b, мм (расчет)

Толщина в зоне контакта, мм

Момент, М, кгм (экспер)

Момент, М, кгм (расчет)

1

Полоса, АМг6М

20×1,95 мм

25,0

1,0

0,6

1,93

1,29

1,15

2

37,5

1,5

0,9

1,90

1,17

2,0

3

50,0

2,0

1,6

1,80

2,04

3,4

4

Труба Д16Т

Ø 30×10×1,5

50,0

1,0

0,9

1,45

1,09

1,9

5

100,0

1,8

1,3

1,40

1,53

2,7

6

Полоса Д16Т

20×0,95 мм

50

1,0

0,6

0,93

1,50

2,4

7

75

1,5

0,9

0,90

2,18

3,7

8

Труба АМг6М

Ø 50×24×2,1

41,7

1,2

0,94

2,05

1,63

2,2

9

62,5

1,5

1,33

1,95

2,21

3,1

Вывод

Из таблицы видно, что расчетные значения крутящего момента отражают физические закономерности процесса, однако превышают экспериментальные значения примерно в 1,5–2,0 раза. Это связано с приближенной зависимостью, которую (по результатам экспериментов) можно уточнить, введя в нее корректирующий коэффициент К = 0,6–0,7. С другой стороны, повышенные расчетные значения крутящего момента удовлетворяют практическим требованиям, т.к. не требуется введение так называемого коэффициента запаса по моменту (мощности) при проектировании установок для раскатки труб.

Рецензенты:

Гагарина Л.Г., д.т.н., профессор, заведующая кафедрой «Информатика и программное обеспечение вычислительных систем» Национального исследовательского университета МИЭТ, г. Москва;

Лисов О.И., д.т.н., профессор кафедры «Информатика и программное обеспечение вычислительных систем» Национального исследовательского университета МИЭТ, г. Москва.

Работа поступила в редакцию 26.08.2014.