Молекулярная фотоэлектронная спектроскопия и квантово-химические расчеты в приближении теории функционала плотности (ТФП) продолжают оставаться в фокусе научных исследований сложных органических и металлоорганических комплексов. Экспериментальное определение вертикальных потенциалов ионизации (ПИ) не всегда возможно из-за низкой летучести большинства таких соединений. В этих случаях расчетные методы оценки ПИ с точностью, близкой к экспериментальной, становятся особенно востребованными. Даже для органических соединений оценка вертикальных ПИ в рамках теоремы Купманса в приближении Хартри – Фока не всегда удовлетворительна, а для металлоорганических комплексов с атомами переходных металлов до сих пор не существует надежного и простого способа определения вертикальных ПИ.
Методы ТФП хорошо воспроизводят не только геометрию основного состояния, но и многие фундаментальные свойства молекул, такие как теплоты образования, энергии диссоциации связей, потенциалы ионизации [1, 3, 5, 9, 10]. Привлекательность теории функционала электронной плотности по сравнению с традиционными квантово-химическими методами заключается ещё и в том, что она непосредственно учитывает энергию корреляции и обладает низкой размерностью. Кроме того, согласно современным теоретическим воззрениям, в рамках ТФП существует аналог теоремы Купманса, что позволяет рассматривать орбитальные энергии Кона ‒ Шема как приблизительные вертикальные ПИ [4]. Справедливость последнего утверждения была проверена рядом авторов на примере некоторых атомов, простых органических и неорганических молекул [6, 7]. Однако систематического сравнения экспериментальных ПИ и энергий Кона – Шема для сложных молекулярных систем с атомами переходных металлов не проводилось.
Целью работы является разработка относительно простого метода оценки вертикальных ПИ сопряженных ферроценов с помощью квантово-химических расчетов в приближении ТФП.
Материалы и методы исследования
В качестве объектов исследования были выбраны несколько представителей сопряженных ферроценов (ФЦ), такие как винилферроцен (винилФЦ), фенилферроцен (фенилФЦ) и стирилферроцен (стирилФЦ). НеI-фотоэлектронные спектры этих соединений были получены на спектрометре ЭС 3201 при температурах 60–80 °С с разрешением 0,040 эВ.
Ферроцен является типичным представителем класса π-комплексов переходных металлов. Его часто называют «бензолом неорганической химии», подчеркивая схожесть электронных и физико-химических свойств ферроцена и бензола.
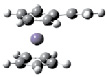
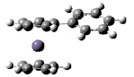
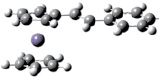
Для оценки вертикальных потенциалов ионизации π-сопряженных ферроценов были проведены расчеты методами ТФП в приближении B3LYP/6-31(d) с полной оптимизацией. Оптимизированная геометрия винилферроцена, фенилферроцена и стирилферроцена представлена на рис. 1.
|
|
|
|
|
ВинилФЦ Fc–CH = CH2 |
ФенилФЦ Fc–C6 H5 |
СтирилФЦ Fc–CH = CH–C6 H5 |
Рис 1. Геометрия винилферроцена, фенилферроцена и стирилферроцена согласно ТФП расчетам в приближении B3LYP/6-31g(d)
Результаты исследования и их обсуждение
Ферроцен
Электронная структура ферроцена изучена достаточно хорошо как методами ФЭ спектроскопии, так и квантово-химическими методами [8]. Согласно этим данным первая и вторая полосы ФЭ спектра отвечают ионизации молекулярных орбиталей (МО) 1e2g и 2a1g типа симметрии – точечная группа симметрии комплекса D5h. Первая МО образована в основном dxy и 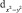 атомными орбиталями (АО) железа, лежащими в плоскости XY и на 80 % локализованными на атоме Fe. Вторая МО – практически «чистая»
атомными орбиталями (АО) железа, лежащими в плоскости XY и на 80 % локализованными на атоме Fe. Вторая МО – практически «чистая» 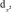 – АО Fe. Вероятность фотоионизации двукратно вырожденной МО 1e2g должна в два раза превосходить вероятность ионизации a1g – МО, что в ФЭ спектре проявляется в соотношении площадей полос. Третья и четвертая полосы с потенциалами ионизации 8,76 и 9,27 эВ соответствуют удалению электронов из МО типа 1e1u и 1e1g, локализованных в основном на С5Н5 лигандах. Молекулярная орбиталь 1e1g представляет собой связывающую комбинацию 1e1g π МО димера (С5Н5)2 и d(yz), d(xz) АО Fe. Таким образом, электроны, занимающие эти МО, делокализованы по p – системе колец и 3d – АО Fe и обеспечивают сильную химическую связь в ферроцене.
– АО Fe. Вероятность фотоионизации двукратно вырожденной МО 1e2g должна в два раза превосходить вероятность ионизации a1g – МО, что в ФЭ спектре проявляется в соотношении площадей полос. Третья и четвертая полосы с потенциалами ионизации 8,76 и 9,27 эВ соответствуют удалению электронов из МО типа 1e1u и 1e1g, локализованных в основном на С5Н5 лигандах. Молекулярная орбиталь 1e1g представляет собой связывающую комбинацию 1e1g π МО димера (С5Н5)2 и d(yz), d(xz) АО Fe. Таким образом, электроны, занимающие эти МО, делокализованы по p – системе колец и 3d – АО Fe и обеспечивают сильную химическую связь в ферроцене.
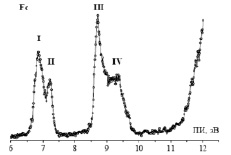
Рис. 2. НеI фотоэлектронный спектр ФЦ
На рис. 2 представлен экспериментальный ФЭ спектр ФЦ. В табл. 1 представлены ПИ, энергии МО, величина дефекта Купманса (DK), характер МО и вклады в МО 3d-AO Fe и 2p AO C лигандов. Величина дефекта Купманса равна по определению сумме расчетных энергий МО εi и экспериментальных ПИ (DK = εi + ПИi) и является мерой отклонения расчетных значений εi от экспериментальных вертикальных ПИ. Из табл. 1 видно, что DK зависит от вклада 3d-AO Fe в МО. Так, для локализованных на органических циклопентадиенильных (ЦП) лигандах, DK равен 2,1 эВ, и уменьшается при увеличении вклада 3d-AO Fe. Этот эффект был замечен нами и при анализе производных ферроценов.
Таблица 1
ПИ и валентные МО ферроцена в симметрии D5d согласно расчетам теории функционала плотности (B3LYP/6-31G(d))
|
Полоса |
ПИ, эВ |
Энергия МО, эВ |
DK, эВ |
Вклады АО в МО (%) |
Характер МО |
|
|
Fe |
Cp |
|||||
|
I |
6,85 |
–5,149 –5,149 |
1,70 |
46,6 50,0 |
53,4 50,0 |
|
|
II |
7,21 |
–5,999 |
1,21 |
93,0 |
7,0 |
|
|
III IV |
8,76 9,27 |
–6,669 –7,171 |
2,09 2,10 |
6,0 25,7 |
94,0 74,3 |
|
Винилферроцен
При введении заместителя в верхнее Cp-кольцо ФЦ его локальная симметрия понижается до C2V и π-МО преобразуются по неприводимым представлениям  и b1-типа, а электронная конфигурация ФЦ из
и b1-типа, а электронная конфигурация ФЦ из
…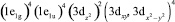
трансформируется в
…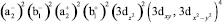 ,
,
причем верхние индексы + и – служат для обозначения π-МО, связывающего и разрыхляющего характера относительно плоскости σh ферроцена. Как показывают ТФП расчеты винилФЦ и других производных ФЦ, активной для π-сопряжения с π-заместителем будет только одна 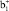 -π-МО, локализованная на верхнем Cp-кольце ферроценила. Орбитали
-π-МО, локализованная на верхнем Cp-кольце ферроценила. Орбитали 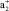 - и
- и  π-типа имеют узловую плоскость, проходящую через место замещения, поэтому МО этого типа не будут взаимодействовать с p-МО заместителей, и их энергия останется такой же, как в ФЦ. Поскольку МО
π-типа имеют узловую плоскость, проходящую через место замещения, поэтому МО этого типа не будут взаимодействовать с p-МО заместителей, и их энергия останется такой же, как в ФЦ. Поскольку МО 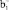 -типа полностью локализована на нижнем Cp-кольце, то только
-типа полностью локализована на нижнем Cp-кольце, то только 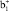 -МО, имеющая максимальную электронную плотность в месте замещения, может эффективно взаимодействовать с p-МО заместителей, давая две новых π-МО, разрыхляющего
-МО, имеющая максимальную электронную плотность в месте замещения, может эффективно взаимодействовать с p-МО заместителей, давая две новых π-МО, разрыхляющего 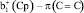 и связывающего
и связывающего 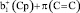 характера, приводя к появлению полос III и VI в спектре винил ФЦ (рис. 3). Полученные результаты и их интерпретация хорошо согласуются с литературными данными для винил ФЦ [2]. Для анализа перекрывающихся полос была применена методика разложения ФЭ спектра на отдельные спектральные компоненты, которые аппроксимировались гауссовскими функциями (ГФ).
характера, приводя к появлению полос III и VI в спектре винил ФЦ (рис. 3). Полученные результаты и их интерпретация хорошо согласуются с литературными данными для винил ФЦ [2]. Для анализа перекрывающихся полос была применена методика разложения ФЭ спектра на отдельные спектральные компоненты, которые аппроксимировались гауссовскими функциями (ГФ).
В табл. 2 представлены ПИ, значения максимумов гауссовских компонент (ПИ*), энергии МО, величины дефекта Купманса, характер МО и вклады в МО 3d Fe AO и 2pС AO винильного фрагмента. Из табл. 2 видно, что DK для локализованных на органических ЦП лигандах, равен 2,1–2,2 эВ, и при увеличении вклада 3d-AO Fe уменьшается, в полном соответствии с данными для незамещенного ФЦ.
Фенилферроцен
При введении в качестве заместителя фенильной группы число полос в ФЭ спектре фенилФЦ по сравнению с ФЦ должно увеличиться на 2 полосы, т.е. в области ПИ 8–10,5 эВ должно располагаться 6 полос. Эти полосы хорошо видны после разложения перекрывающихся полос IV–V (рис. 4). В табл. 3 представлены ПИ, значения максимумов гауссовских компонент – ПИ*, энергии МО, величины дефекта Купманса, характер МО и вклады в МО 3d Fe AO и 2pС AO фенильного фрагмента. Анализ табл. 3 показывает, что DK для шести МО, локализованных на органических лигандах, равен 2,1–2,3 эВ, и при увеличении вклада 3d-AO Fe уменьшается до 1,0–1,6 эВ. Эти значения DK согласуются с данными для незамещенного ФЦ и винилФЦ.
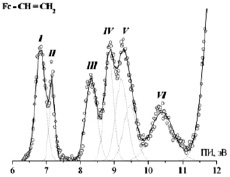
Рис. 3. НеI-фотоэлектронный спектр винил-ФЦ
Таблица 2
ПИ и валентные МО винилферроцена в симметрии C1 по результатам расчетов методом ТФП (B3LYP/6-31G(d))
|
Полоса |
ПИ, эВ |
ПИ*, эВ |
Энергия МО, эВ |
DK, эВ |
Вклады АО в МО (%) |
Характер МО |
|
|
Fe |
R |
||||||
|
I |
6,85 |
6,83 6,83 |
–5,15 –5,21 |
1,68 1,62 |
40,0 48,0 |
2,0 0,1 |
|
|
II |
7,15 |
7,17 |
–6,03 |
1,14 |
67,0 |
9,3 |
|
|
III |
8,31 |
8,33 |
–6,13 |
2,20 |
57,5 |
15,5 |
b1(Cp) – π(C = C) |
|
IV V |
8,89 9,27 |
8,85 9,21 9,46 |
–6,72 –7,07 –7,24 |
2,13 2,14 2,22 |
5,9 23,5 26,4 |
0,2 4,7 0,1 |
b1(Cp’)
|
|
VI |
10,31 |
10,41 |
–8,07 |
2,24 |
7,5 |
43,3 |
b1(Cp) + π(C = C) |
Примечание. * Вертикальные потенциалы ионизации, соответствующие максимумам ГФ.
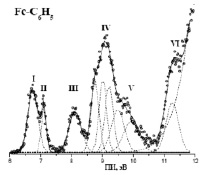
Рис. 4. НеI-фотоэлектронный спектр фенил-ФЦ
Таблица 3
ПИ и валентные МО фенилФЦ в симметрии C1 согласно расчетам методом ТФП (B3LYP/6-31G(d))
|
Полоса |
ПИ, эВ |
ПИ*, эВ |
Энергия МО, эВ |
DK, эВ |
Вклады АО в МО (%) |
Характер МО |
|
|
Fe |
R |
||||||
|
I |
6,74 |
6,74 6,74 |
–5,14 –5,20 |
1,60 1,54 |
42,7 44,8 |
2,5 0,5 |
3dxy(Fe) |
|
II |
7,09 |
7,09 |
–6,11 |
0,98 |
81,9 |
4,8 |
|
|
III |
8,04 |
8,09 |
–5,96 |
2,13 |
28,5 |
33,1 |
b1(Cp) – b1(Ph) |
|
IV |
9,08 |
8,75 9,01 9,21 9,49 |
–6,67 –6,78 –7,03 –7,23 |
2,08 2,23 2,18 2,26 |
3,4 3,1 18,3 30,2 |
40,3 55,3 9,9 0,5 |
a2(Ph) + b1(Cp’)
|
|
V |
10,31 |
10,41 |
–8,07 |
2,24 |
7,5 |
43,3 |
b1(Cp) + b1(Ph) |
Примечание. * Вертикальные потенциалы ионизации, соответствующие максимумам ГФ.
Стирилферроцен
Замена фенильной группы на стирильную приводит к увеличению количества π-полос в фотоэлектронном спектре до 7. Ионизация этих семи π-МО формирует центральную зону ФЭ спектра в области 7,5–11,0 эВ. Величина энергетического расщепления «активных» МО в стирилферроцене (полосы III и V) прекрасно описывается разностью расчетных энергий МО, которая равна 2,72 эВ и совпадает с экспериментальным значением (табл. 4). Ионизация 5 неактивных, т.е. практически не участвующих в π-π-взаимодействии молекулярных орбиталей формирует интенсивную центральную ФЭ полосу IV. Энергии этих пяти МО, как и в случае других сопряженных ферроценов, оказались расположенными в достаточно узком энергетическом диапазоне 6,7–7,3 эВ, соответствующем энергиям МО 1e1g и 1e1u – МО свободного ферроцена. HeI-фотоэлектронный спектр стирилферроцена представлен на рис. 5.
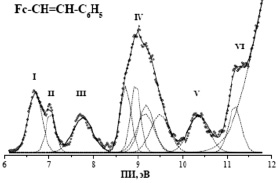
Рис. 5. НеI-фотоэлектронный спектр стирилферроцена
В табл. 4 представлены ПИ, значения максимумов гауссовских компонент – ПИ*, энергии МО, величины дефекта Купманса, характер МО и вклады в МО 3d Fe AO и 2pС AO стирильного фрагмента. Анализ табл. 4 показывает, что первые 3 МО, состоящие преимущественно из 3d-AO Fe, имеют DK порядка 1,0–1,6 эВ. Отметим, что энергии МО всех последующих семи π-МО отличаются от экспериментальных ПИ на постоянную величину 2,1 ± 0,1 эВ независимо от вклада АО Fe. Эти значения DK согласуются с данными для всех рассмотренных ранее производных ферроцена.
Таблица 4
Валентные МО Fc–CH = CH–C6H5 в симметрии C1 согласно расчетам методом ТФП (B3LYP/6-31G(d))
|
Полоса |
ПИ, эВ |
ПИ*, эВ |
Энергия МО, эВ |
DK, эВ |
Вклады АО в МО (%) |
Характер МО |
|
|
Fe |
R |
||||||
|
I |
6,67 |
6,67 6,67 |
–5,09 –5,23 |
1,58 1,44 |
37,6 46,8 |
10,1 0,4 |
3dxy(Fe) |
|
II |
7,01 |
7,01 |
–6,12 |
0,89 |
91,0 |
1,2 |
|
|
III |
7,67 |
7,75 |
–5,62 |
2,13 |
21,8 |
36,5 |
b1(Cp) – π(C = C) + b1(Ph) |
|
IV |
9,03 |
8,72 8,92 9,05 9,23 9,49 |
–6,73 –6,74 –6,92 –7,26 –7,28 |
1,99 2,18 2,13 1,97 2,21 |
0,1 5,8 8,8 24,8 21,7 |
98,3 1,8 22,7 3,9 22,2 |
a2(Ph)
b1(Cp′)
|
|
V |
10,29 |
10,36 |
–8,34 |
2,02 |
4,1 |
65,8 |
b1(Cp) + π(C = C) + b1(Ph) |
Примечание. * Вертикальные потенциалы ионизации, соответствующие максимумам ГФ.
Дефект Купманса
Данные табл. 2–6 свидетельствуют о том, что для МО с большими или доминирующими вкладами 3d АО Fe (70–90 %) характерны усреднённые значения дефекта Купманса – 1,63 ± 0,10 эВ для МО 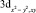 – типа и 1,01 ± 0,08 эВ для МО
– типа и 1,01 ± 0,08 эВ для МО 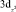 -типа, в то время как для МО p-типа с небольшими (от 0 до 30 %) вкладами 3d АО Fe дефект Купманса практически постоянен и равен 2,18 ± 0,10 эВ. На рис. 6 представлена зависимость DK от вклада 3d-АО Fe в МО сопряженных ферроценов. Полученная зависимость хорошо аппроксимируется линейной функцией DK = 2,44 – 0,018∙N(3d Fe), R = 0,999.
-типа, в то время как для МО p-типа с небольшими (от 0 до 30 %) вкладами 3d АО Fe дефект Купманса практически постоянен и равен 2,18 ± 0,10 эВ. На рис. 6 представлена зависимость DK от вклада 3d-АО Fe в МО сопряженных ферроценов. Полученная зависимость хорошо аппроксимируется линейной функцией DK = 2,44 – 0,018∙N(3d Fe), R = 0,999.
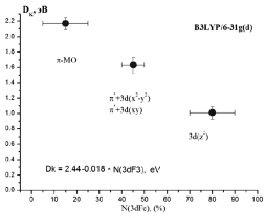
Рис. 6. Зависимость DK от вклада 3d-АО Fe в МО сопряженных ферроценов
Характеризуя полученные результаты, можно утверждать, что установленные закономерности поведения DК позволяют достаточно просто оценивать вертикальные ПИ в изучаемом классе соединений с экспериментальной точностью. Действительно, для расчета вертикальных ПИ в соответствии с уравнением
ПИi = –εi + DK
необходимо провести расчет одноэлектронных энергий МО (энергий Кона – Шема) методом B3LYP/6-31G(d), определить относительный вклад 3d АО Fe в каждую валентную МО КШ и выбрать соответствующее значение дефекта Купманса для каждой МО в соответствии с линейным уравнением DK = 2,44 – 0,018∙N(3dFe).
Выводы
В работе было показано, что энергии МО, рассчитываемые в рамках ограниченного метода ТФП в приближении B3LYP/6-31G(d)), могут описывать экспериментальные потенциалы ионизации производных ферроцена с точностью до энергетической поправки DK, зависящей от вклада 3d-АО железа в МО, что позволяет более обоснованно интерпретировать ФЭ спектры комплексов переходных металлов.
Рецензенты:
Рябчук В.К., д.ф.-м.н., профессор, Санкт-Петербургский государственный университет, г. Санкт-Петербург;
Барабан А.П., д.ф.-м.н., профессор, Санкт-Петербургский государственный университет, г. Санкт-Петербург.
Работа поступила в редакцию 05.08.2014.




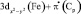
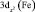
 ,
, 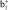 – π(Cp)
– π(Cp)
 ,
,  > – π(Cp) + 3dyz, 3dxz(Fe)
> – π(Cp) + 3dyz, 3dxz(Fe)
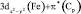
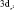 (Fe)
(Fe)
 (Fc)
(Fc)
 (Fc)
(Fc)
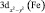
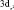 (Fe)
(Fe)
 (Fc) – a2(Ph)
(Fc) – a2(Ph)
 (Fc)
(Fc)
 (Fc)
(Fc)
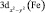
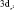 (Fe)
(Fe)
 (Fc)
(Fc)
 (Fc)
(Fc)
 (Fc) – b1 (Ph)
(Fc) – b1 (Ph)