В области создания роботов концепция эндоскелета находит теоретическое и практическое воплощение. Большое число степеней свободы, присущее системам с эндоскелетной структурой, имеет свои недостатки, обусловленные их же достоинствами. Большое число степеней свободы обуславливает потенциальную неустойчивость системы, которая должна уравновешиваться более сложной системой управления. В связи с этим в настоящее время все большее развитие получает идея синтеза эндоскелета с экзоскелетом, причем не панцирного, а актуаторного типа, усиливающего функции основного.
В биологических системах эндоскелетного типа структуры, передающие энергию мышц, представляют собой кинематические цепи шарнирно-стержневого типа. Основные формы силового взаимодействия стержней в шарнирах – это рычаги первого и второго рода.
Создание экзоскелетов с различными функциями для гражданских целей может со временем сделать экзоскелет даже более распространенной машиной, чем велосипед.
Во многих странах, не только обладающих большим научно-техническим потенциалом (Россия, США, Германия, Япония и др.), но и в Австралии, Новой Зеландии, ЮАР, Корее и др. проводятся серьезные исследования по созданию антропоморфных роботов и экзоскелетов [1–5, 7–10].
На основе новых технологий и материалов можно будет в перспективе рассчитать и сделать экзоскелет и антропоморфного робота, полностью адекватным движениям человека и с гораздо меньшими энергетическими затратами, чем современные роботы, созданные на основе твердого тела. Предложим перспективное описание подобной модели.
Исследуем вопрос о существовании и единственности решения задачи Коши полученной ранее системы дифференциальных уравнений движения для механической системы типа экзоскелета с деформируемыми звеньями [1–3]. Удобно проводить анализ на простейшей модели. Поэтому составим дифференциальные уравнения движения для однозвенного механизма.
Для исследования плоского движения экзоскелета с деформируемыми звеньями в одноопорной фазе введем неподвижную правую декартову систему координат xyz с началом в точке O, рассмотрим плоскость xy, в которой происходит движение центра масс.
Проведем анализ одного звена с управлением в точке крепления. Подобная модель может иметь практическое применение для предотвращения разрушения звена при значительных нагрузках или в медицине при переломах костей. Система имеет одно весомое звено АВ. Оно является упругим, и длина стержня является функцией времени: l1 = l1(t). На рисунке схематично изображено звено и введены соответствующие обозначения.
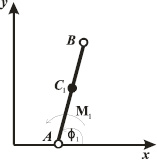
Схема кинематического звена стержневой механической системы
Пусть длина рассматриваемого звена экзоскелета AB = l1. Положение однозначно определяется углом φ1 и длиной стержня l1. Рассматриваемая система имеет две степени свободы. Обозначим через M1 момент, развиваемый в шарнире. Центр масс звена находится в точке С1. Его положение будем задавать в виде отношения длины от начала звена до центра его масс ко всей длине звена, через множитель n1, (0 < n1 < 1). Такой способ следует из того, что для человека положения центров масс конечностей определяются эмпирическим путем и задаются в виде отношения одной части звена к другой [1], кроме того, он позволяет учесть изменение положения центра масс во время движения через известные деформации звена. Масса звена – m1. Момент инерции звена, относительно оси, проходящей через точку А перпендикулярно плоскости движения – I1. При расчетах и моделировании движения экзоскелета все вышеприведенные характеристики берутся равными соответствующим экспериментальным данным человека.
Так как активных внешних сил нет, то движение происходит только под действием внутренних сил и внешних реакций. Связь в точке A реализуется в виде идеального шарнира и является двусторонней или удерживающей. Момент M1, действующий в системе, изображен на рисунке.
Записав выражение элементарной работы δA для сил, приложенных к системе, получаем обобщенные силы.
Q1 = M1;
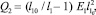 (1)
(1)
где 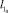 – длина недеформированного звена; E1 – модуль Юнга материала, из которого изготовлен элемент экзоскелета.
– длина недеформированного звена; E1 – модуль Юнга материала, из которого изготовлен элемент экзоскелета.
Пользуясь формализмом Лагранжа, получим систему уравнений движения рассматриваемой стержневой системы, описывающую изменение угловых координат звеньев и деформаций звеньев механизма.
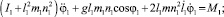 (2)
(2)
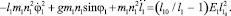 (3)
(3)
Общее решение системы уравнений движения зависит от 4 произвольных постоянных. Чтобы однозначно определить движение, требуется задать начальные условия. Для угловых координат формулы (4), для изменений длин звеньев – (5).
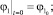
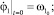 (4)
(4)
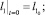
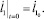 (5)
(5)
Уравнения (2), (3) – дифференциальные уравнения движения для однозвенной механической модели.
Таким образом, записана замкнутая система дифференциальных уравнений. Замкнутость системы дифференциальных уравнений означает, что количество уравнений, с учетом порядка, совпадает с количеством искомых функций, имеются все начальные условия, числовые значения всех констант определены, все это позволяет получить численное решение задачи Коши для записанной системы уравнений.
Используем для решения поставленной задачи исследования существования и единственности сформулированной задачи Коши теорему Пикара. Приведем формулировку данной теоремы [6]:
Теорема (Пикара): Пусть правые части системы
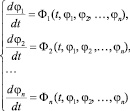 (6)
(6)
удовлетворяют в замкнутой ограниченной области R вида |t – t0| ≤ a; 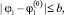
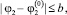 …,
…, 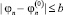 (где a и b – заданные положительные числа) следующим двум условиям:
(где a и b – заданные положительные числа) следующим двум условиям:
а) функции Фk (k = 1, 2, …, n) непрерывны по всем своим аргументам и, следовательно, удовлетворяет в замкнутой ограниченной области R условиям
|Фk(t, φ1, φ2, …, φn)| ≤ M (k = 1,2, …, n), (7)
где M – постоянное положительное число, а (t, j1, j2, …, jn) – любая точка области R;
б) функции Фk (k = 1,2, …, n) удовлетворяют условию Липшица относительно аргументов φ1, φ2, …, φn, то есть
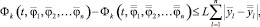 (8)
(8)
где L – постоянное положительное число (константа Липшица), а 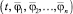 и
и 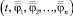 – любые две точки области R.
– любые две точки области R.
Тогда система дифференциальных уравнений (6) имеет единственное решение:
φ1 = φ1(t); φ2 = φ2(t); …; φn = φn(t), (9)
удовлетворяющее начальным условиям:
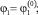
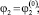 ...;
...; 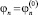 , при t = t0, (10)
, при t = t0, (10)
где t0, 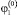 ,
, 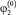 , …,
, …, 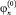 – некоторые заданные постоянные числа.
– некоторые заданные постоянные числа.
Это решение заведомо определено и непрерывно дифференцируемо в интервале
|t – t0| ≤ h, (11)
где
h = min(a, b/M), (12)
и не выходит при этих значениях t из области R, то есть
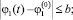
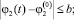 …;
…; 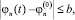 при |t – t0| ≤ h. (13)
при |t – t0| ≤ h. (13)
Замечание. Условие Липшица представляет собою оценку роста правых частей системы (6) по аргументам φ1, φ2, …, φn, причем из (8) следует, что эта оценка равномерна относительно t в интервале |t – t0| ≤ a.
Условие Липшица будет, в частности, выполнено, если все функции Фk (k = 1, 2, …, n) имеют ограниченные в области R частные производные по переменным φ1, φ2, …, φn, то есть
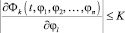 , (k,l = 1,2, …, n), (14)
, (k,l = 1,2, …, n), (14)
где K – некоторое постоянное положительное число, (t, φ1, φ2, …, φn) – любая точка области R.
Если имеется дифференциальное уравнение n-го порядка, разрешенное относительно старшей производной,
φ(n) = Ф(t, φ, φ′, …, φ(n–1) ), (15)
с начальными условиями при t = t0
φ = φ0; φ′ = φ′0 …, φ(n–1) = φ0(n–1) , (16)
то в теореме Пикара условие Липшица заменяется более сильным требованием ограниченности частных производных
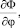
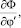 …,
…, 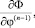 (17)
(17)
где n – порядок дифференциального уравнения.
Так как теорема Пикара выше формулировалась для системы первого порядка, то уравнение n-го порядка приводится к нормальной системе уравнений первого порядка путем введения неизвестных функций.
φ1 = φ, φ2 = φ′, …, φn = φ(n–1) . (18)
Тогда уравнение (15) принимает вид
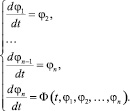 (19)
(19)
Для того, чтобы воспользоваться данной теоремой, разрешим уравнения движения однозвенного механизма (2) и (3) относительно старших производных:
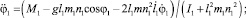 (20)
(20)
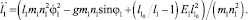 (21)
(21)
Найдем частные производные первого порядка для правых сторон уравнений (20) и (21) по φ1, l1, 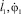 .
.
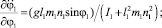
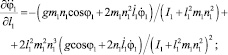
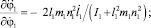
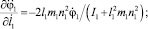
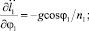
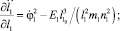
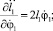
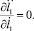 (22)
(22)
Очевидно, что все полученные частные производные непрерывны в некоторой области D, зависящей от параметров системы. Тогда при начальных условиях (4) и (5) данная система дифференциальных уравнений, в соответствии с теоремой Пикара, имеет единственное решение задачи Коши.
Решение существует и единственно на промежутке, который можно оценить. Проведем численную оценку области существования и единственности решения, используя реальные данные из биомеханики, измерений и эксперимента, проведенных нами [1]. При этом будем использовать максимальные значения величин. Здесь не будем рассматривать правые части исходных уравнений, а ограничимся только левой частью, то есть рассмотрим однородную систему уравнений, соответствующую уравнениям (2) и (3). Это связано с тем, что управление системой, как и учет деформаций, могут быть осуществлены различными способами. Это видно и из полученных частных производных, в которых управляющие моменты, которые задаются как функции времени, отсутствуют. Соответственно, при этом допущении
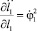 .
.
Числовые значения констант взяты из эксперимента и соответствуют данным для конкретного человека [1]. В качестве первого звена рассматривается стопа опорной ноги. Они имеют значения: масса m1 = 1,13 кг, момент инерции I1 = 0,01 кг⋅м2, множитель, задающий положение центра масс n1 = 0,5585, ускорение свободного падения g = 9,81 м/с2. Угол φ1 и длина звена l1 являются переменными (функции времени), определялись экспериментально и задавались в виде интерполяционных многочленов для одной фазы движения, на промежутке времени 0 ≤ t ≤ 0,36 c. В результате расчетов максимальные абсолютные значения частных производных равны: 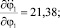
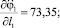
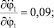
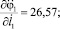
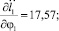
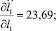
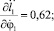
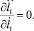
В итоге получили ограниченные в области R частные производные по переменным φ1, l1, 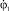 ,
,  на промежутке 0 ≤ t ≤ 0,36 c. Это доказывает существование и единственность решения задачи Коши для исходной системы дифференциальных уравнений (2) и (3).
на промежутке 0 ≤ t ≤ 0,36 c. Это доказывает существование и единственность решения задачи Коши для исходной системы дифференциальных уравнений (2) и (3).
Проверяя полученный результат для двухзвенной механической системы, также получаем непрерывность и ограниченность всех частных производных. Здесь он не приводится ввиду громоздкости получаемых выражений. Ранее получены обобщения уравнений для n-звенного механизма [2, 3] и установлено, что их структура не отличается от уравнений, рассмотренных выше. Поэтому, проделывая всё по аналогии с уже рассмотренным случаем, приходим к заключению, что решение задачи Коши существует и единственно для n-звенного экзоскелета.
Таким образом, доказано существование и единственность решения задачи Коши для системы дифференциальных уравнений движения экзоскелета с деформируемыми звеньями.
Работа выполнена при финансовой поддержке РФФИ (грант № 13-01-97512 р_центр_а).
Рецензенты:
Денисов В.Н., д.т.н., заведующий кафедрой высшей математики, филиал ФГБОУ ВПО НИУ «МЭИ», г. Смоленск;
Мазалов М.Я., д.ф.-м.н., доцент кафедры высшей математики, филиал ФГБОУ ВПО НИУ «МЭИ», г. Смоленск.
Работа поступила в редакцию 05.08.2014.



