Интерес к проблемам волновой динамики пузырьковых жидкостей, протекающей в эластичных трубках, обусловлен важностью применения результатов исследований к проблемам расчета гидравлических систем в летательных аппаратах, в нефтяной и газовой промышленности, химической технологии.
Целью нашей работы является развитие теории волновых течений пузырьковых жидкостей в трубках с эластичными стенками.
Постановка задачи и система уравнений. Рассмотрим одномерные волновые возмущения, распространяющиеся в трубке малого радиуса, заполненной пузырьковой жидкостью.
Стенки трубки считаем эластичными. На рис. 1 представлено схематическое изображение системы, которое иллюстрирует трубку толщиной h, длиной L и радиусом a0 (L >> a0). Возмущения в системе возникают вследствие воздействия давлением по торцу трубки.
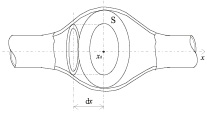
Рис. 1. Схема задачи
Полагая общепринятые допущения для пузырьковых жидкостей, запишем основные уравнения для описания движения волн в пузырьковой жидкости в трубке с эластичными стенками. Макроскопические уравнения сохранения масс, числа пузырьков, импульсов в односкоростном приближении имеют вид [1]
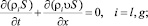
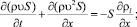
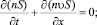
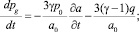
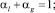
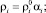
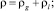
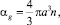
здесь и далее ρi – плотность фазы; n – число пузырьков; S – площадь поперечного сечения трубки; υ – скорость; αi – объемное содержание фазы; а – радиус пузырьков; γ – показатель адиабаты для газа; q – тепловой поток; pg – давление газа.
Будем считать жидкость акустически сжимаемой, газ калорически совершенным:
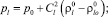
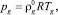
здесь 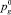 – начальное давление жидкости; R – газовая постоянная; Tg – температура газа.
– начальное давление жидкости; R – газовая постоянная; Tg – температура газа.
При описании радиального движения в соответствии с уточнением, предложенным в [2], будем полагать, что w = wR + wA, где wR – определяется из уравнения Релея – Ламба, а wA – определяется из решения задачи о сферической разгрузке на сфере радиуса a в несущей жидкости в акустическом приближении:
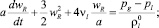
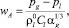
где vl – вязкость жидкости; Cl – скорость звука в «чистой» жидкости.
Тепловой поток задаем следующим приближенным конечным соотношением [3]:
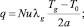
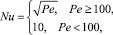
где 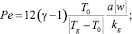
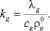
Температура газа в пузырьках меняется по закону
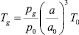 .
.
Рассмотрим два случая: будем считать, что стенки трубки помимо эластичных свойств обладают массой, обусловливающей радиальную инерцию стенок при распространении волновых возмущений, и исследуем динамику нелинейных волн в эластичной трубке без инерционных свойств ее стенок. Закон Гука для эластичной трубки имеет вид [4]
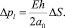
В случае учета радиальной инерции стенок трубки считаем, что радиус трубки меняется согласно уравнению
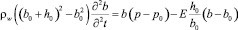 ,
,
где E – модуль Юнга; h0 – толщина стенки трубки; b0 – начальное значение внутреннего радиуса трубки; ρw – плотность материала трубки.
Для численного анализа удобнее пользоваться системой уравнений, записанной в лагранжевых координатах, запишем приведенную выше систему уравнений в лагранжевых переменных:
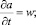
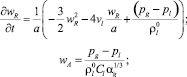
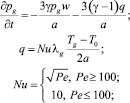
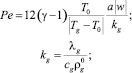
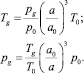
Для случая отсутствия радиальной инерции стенок трубки давление жидкости и объемное содержание пузырьков, изменение поперечных размеров трубки определяется следующими частными производными:
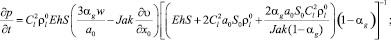
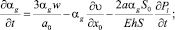
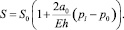
Для случая эластичных стенок трубки с радиальной инерцией давление в жидкости, объемное содержание пузырьков, изменение радиуса стенок трубки определяются следующим образом:
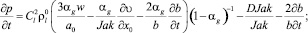
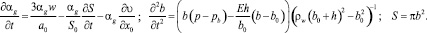
Системы уравнений решаются численно по явной схеме с использованием метода конечных разностей [5].
Начальные и граничные условия. Нелинейные волны, возникающие в трубке, распространяются вдоль положительного направления оси z до противоположного торца трубки, ограниченного жесткой стенкой: z = L: υz = 0, 0 < a0 < R.
Начальные условия для остальных входных параметров соответствуют следующим:
t = 0: pl = p0, S = S0, pg = p0, wR = 0, a0 = 1 мм или 0,1 мм.
Возмущения в трубе возникают вследствие воздействия по торцу трубки давлением согласно условиям при t* = 1 мс и Δp = 1 атм:
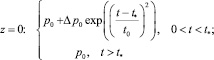 (1)
(1)
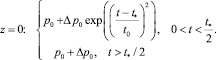 (2)
(2)
Обсуждение результатов
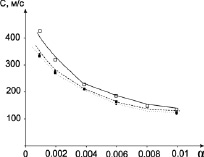
Рис 2. Зависимость скорости нелинейных волн в пузырьковой жидкости от концентрации пузырьков
На рис. 2 представлены графики, иллюстрирующие влияние концентрации пузырьков на скорость распространения нелинейных волн. Сплошная линия соответствует значениям скоростей для волн, распространяющихся в трубке с жесткими стенками, пунктирная линия – случаю распространения волн в трубке с поликарбонатными стенками с учетом радиальной инерции стенок, точечная линия – случаю распространения волн в трубке с поликарбонатными стенками без учета радиальной инерции. Из рис. 2 видно, что по мере увеличения концентрации пузырьков скорость нелинейных волн снижается, значения скоростей для волн, распространяющихся в поликарбонатных трубках с учетом и без учета инерции стенок трубки, близки друг другу, их значения по мере увеличения концентрации пузырьков.
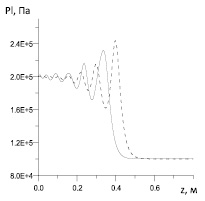
На рис. 3 представлены эпюры давления в жидкости в момент времени 1,5 мс, графики получены при различных радиусах пузырьков: на рис. 3, а эпюры построены при a0 = 1 мм, на рис. 3, б – при a0 = 0,1 мм приближаются к значению скорости для волн в трубке с жесткими стенками. Сплошная линия на рис. 3 соответствует случаю распространения нелинейных волн в трубке с поликарбонатными стенками с учетом радиальной инерции стенок трубки, пунктирная линия – случаю распространения волн в трубке с жесткими стенками.
Из графиков видно, что при радиусе пузырьков a0 = 1 мм осцилляционная структура волны характерна для нелинейных волн, распространяющихся в жесткой трубке и трубке, стенки которой обладают эластичностью и радиальной инерцией. Пульсации давления связаны здесь главным образом с изменением радиуса пузырьков жидкости во фронте распространяющейся волны.
 а
а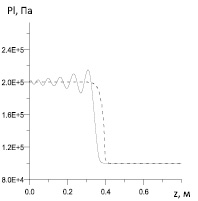 б
б
Рис. 3. Зависимость давления двухфазной жидкости от координаты в момент времени 1,5 мс при различных радиусах пузырьков: а – случай соответствует радиусу пузырьков 1 мм; б – случай – радиусу пузырьков 0,1 мм
При уменьшении радиуса пузырьков в 10 раз для волн в трубке с жесткими стенками изменение давления в жидкости вдоль трубы носит монотонный характер, а динамика волн в поликарбонатной трубке с радиальной инерцией стенок сохраняет осцилляционную структуру. Данный эффект обусловлен тем, что более мелкие воздушные пузырьки слабее воздействуют на жидкость, передавая ей дополнительное давление, таким образом, процессы связанные с диссипацией на пузырьках, межфазным взаимодействием оказывают на динамику волны незначительное влияние. Доминирующая роль на процесс формирования и эволюции волны здесь переходит к радиальной инерции стенок трубки.
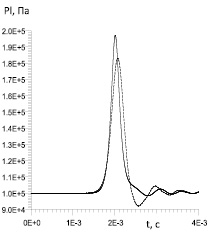
На рис. 4 представлены графики изменения давления в жидкости от времени в фиксированной точке, находящейся в 500 см от торца трубки, по которому производилось первоначальное воздействие. Графики получены при различных значениях концентраций пузырьков: на рис. 4, а графики соответствуют α = 0,001, на рис. 4,б – α = 0,01. Пунктирная линия на рис. 4 соответствует случаю распространения нелинейных волн в трубке с поликарбонатными стенками с учетом радиальной инерции стенок трубки, сплошная линия – случаю распространения волн в трубке с эластичными стенками без учета инерции стенки. Из рис. 4 видно, что амплитуды волн давления при концентрации пузырьков α = 0,001 различаются на величину 0,1 атм в случаях распространения волн по трубке с эластичными поликарбонатными стенками с учетом и без учета радиальной инерции стенок, что обусловлено различными способами описания изменения поперечных размеров трубки.
 а
а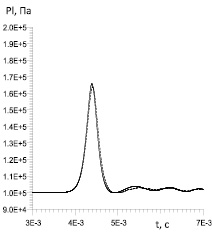 б
б
Рис. 4. Зависимость давления двухфазной жидкости от времени в точке, удаленной от нижнего торца трубы на расстояние z = 500 см, при различных объемных содержаниях пузырьков: а – случай соответствует концентрации пузырьков 0,001; б – случай – концентрации пузырьков 0,01
По мере увеличения концентрации пузырьков (α = 0,01) значение амплитуд волн давления оказывается единым, что обусловлено едиными процессами, протекающими в пузырьковой жидкости, оказывающих первостепенное влияние на динамику волн, распространяющихся в трубке.
Заключение
По результатам исследования сделали следующие выводы: процессы, характерные для пузырьков при распространении волн двухфазной жидкости, оказывают влияние на динамику волн при радиусе пузырьков r = 1 мм, при уменьшении радиуса пузырьков до r = 0,1 мм диссипация на пузырьках и межфазное взаимодействие пренебрежимо малы, радиальная инерция стенок трубки сохраняет свое воздействие на динамику волны. Аналогичная тенденция наблюдается при изменении концентрации пузырьков единого радиуса: при малых концентрациях пузырьков на эволюцию волн давления оказывают большее влияние свойства эластичности стенок трубки, при увеличении концентрации пузырьков динамика волн определяется процессами, протекающими в пузырьковой жидкости. Скорость волн двухфазной жидкости меньше скорости звука, и она убывает с увеличением концентрации пузырьков. Эта тенденция сохраняется и при учете радиальной инерции стенок трубки. Следует отметить, что скорость волн в этом случае близка к значениям данного параметра, характерного для случая отсутствия радиальной инерции у эластичных стенок трубки.
Рецензенты:
Гималтдинов И.К., д.ф.-м.н., профессор, зав. кафедрой «Прикладная математика и механика» Стерлитамакского филиала БашГУ, г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор, зав. кафедрой «Алгебра, геометрия и методика преподавания математики» Стерлитамакского филиала БашГУ, г. Стерлитамак.
Работа поступила в редакцию 05.08.2014.



