В [1] представлена виброизолирующая подвеска двигателя с плавающим участком нулевой жесткости, содержащая в качестве компенсатора жесткости два встречно включенных электромагнита. Там же показано, что при межполюсном расстоянии электромагнитов, превышающем размах колебаний на порядок, силовая характеристика компенсатора может быть принята линейной. Однако линейный компенсатор целесообразно применять в подвесках, где установлены упругие элементы с небольшими коэффициентами жесткости и нет жестких ограничений габаритов подвески. В подвесках, где установлены упругие элементы с большими коэффициентами жесткости и где габариты виброизоляторов ограничены, электромагнитные компенсаторы должны иметь малые габариты при достаточно большом коэффициенте жесткости. Это возможно только при значительном сокращении межполюсного расстояния компенсатора. При этом силовая характеристика компенсатора жесткости получается нелинейной, что необходимо учитывать при определении свойств виброизолирующей подвески. Математическая модель нелинейного электромагнитного компенсатора жесткости выведена в [2].
Результаты исследования и их обсуждение
Как показано в [1], систему перестройки электромагнитного компенсатора жесткости на изменяющуюся нагрузку целесообразно выполнять в виде регулятора напряжения катушек электромагнитов. При этом регулятор может быть как линейным, так и нелинейным звеном. В [1, 2] рассмотрена модель виброизолирующей подвески с электромагнитным компенсатором жесткости, содержащей линейный регулятор подстройки на изменяющуюся внешнюю нагрузку.
Из дифференциального уравнения (1), полученного в [1], видно, что в системах виброизолирующих подвесок с линейным и нелинейным регуляторами присутствует нелинейность.
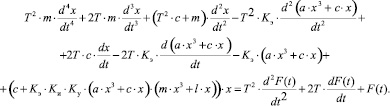 (1)
(1)
Для нелинейных систем характерно наличие режима автоколебаний. Выполним проверку наличия автоколебаний в обоих случаях. В автоматике существуют методы определения режима автоколебаний. Воспользуемся одним из этих методов, алгебраическим методом, показанным в [3].
На основании дифференциального уравнения виброизолятора с линейной системой перестройки (1) составим структурную схему, показанную на рис. 1.
Для того чтобы проверить наличие автоколебаний в системе виброизолирующей подвески линейной системы перестройки, необходимо структурную схему, показанную на рис. 1, преобразовать в одно звено.
Приведем структурную схему, показанную на рис. 1, к одноконтурной схеме.
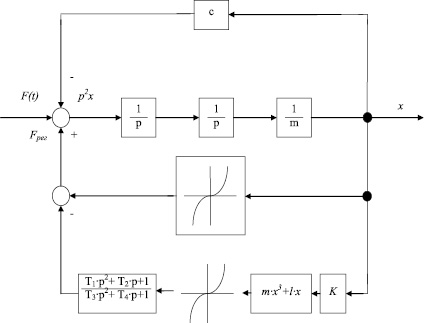
Рис. 1. Структурная схема виброизолирующей подвески с нелинейным инерционным регулятором и с корректирующим звеном
Вид одноконтурной структурной схемы виброизолирующей подвески с нелинейным инерционным регулятором показан на рис. 2.
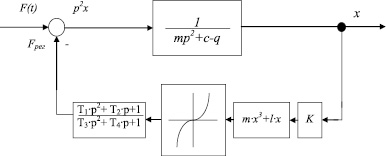
Рис. 2. Одноконтурная структурная схема виброизолирующей подвески с нелинейным инерционным регулятором
На основании структурной схемы виброизолирующей подвески с линейным регулятором, показанной на рис. 2, получим передаточную функцию замкнутой системы:
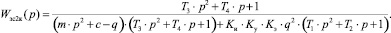 (2)
(2)
Характеристическое уравнение:
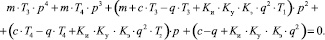 (3)
(3)
Подставим p = jω:
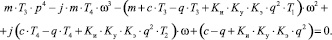 (4)
(4)
Выделим действительную и мнимую части:
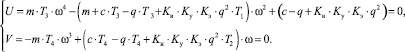 (5)
(5)
Из второго уравнения системы (5)
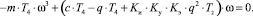 (6)
(6)
Выполнив преобразования уравнения (6), получим
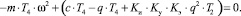 (7)
(7)
Из (7) выразим
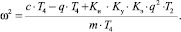 (8)
(8)
Из уравнения (8) определим круговую частоту автоколебаний:
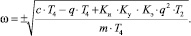 (9)
(9)
Подставив (8) в первое уравнение системы (5), получим
 (10)
(10)
В результате из первого уравнения системы (5) получим
 (11)
(11)
Используя готовый график q(a), полученный в [4], находим амплитуду периодического решения а.
Устойчивость периодического решения проверяется следующим образом:
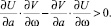 (12)
(12)
Для определения устойчивости периодического решения, согласно критерию (13), необходимо определить производные первого уравнения системы (5) по амплитуде и частоте периодического решения и второго уравнения системы (5) по амплитуде и частоте периодического решения.
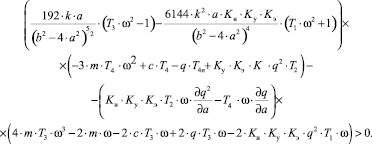 (13)
(13)
Заключение
Если условие (13) выполняется, то периодическое решение устойчиво, то есть автоколебания есть. Разработанная методика будет использована в проверке эффективности работы виброизоляторов с электромагнитным компенсатором жесткости и нелинейной системой перестройки. Практическое применение таких виброизоляторов может стать эффективным средством снижения уровней вибрации на транспорте, в промышленности, на производстве.
Рецензенты:
Расторгуев Г.И., д.т.н., профессор, первый проректор НГТУ, г. Новосибирск;
Щуров Н.И., д.т.н., профессор, заведующий кафедрой электротехнических комплексов (ЭТК), НГТУ, г. Новосибирск.
Работа поступила в редакцию 05.08.2014.



