Существует ряд подходов к рационализации подбора рецептуры и технологии производства композиционных материалов. В общем случае выбор сводится к задачам оптимизации, которые успешно решены в теории оптимального управления сложными техническими системами. К сожалению, авторам известны лишь редкие случаи использования методов теории управления и системного анализа к разработке композитов [1, 5, 7, 9, 12]. Ниже предлагается подход к синтезу композиционных материалов с регулируемыми структурой и свойствами с позиций классической теории оптимального управления. Последовательность этапов синтеза композиционных материалов как сложных систем [7] приводится на рис. 1, в числе основных выделяются:
- техническая постановка задачи и выбор критериев оптимизации;
- построение математических моделей управления в форме системы операторных уравнений (дифференциальных, интегральных, разностных, дифференциально-разностных, дифференциально-интегральных и т.д.).
Математическая модель и пути ее построения определяются степенью изученности рассматриваемой системы, наличием опыта разработки аналогичных систем, полноты знания физических процессов, характеризующих поведение объекта, и осуществляются на основе теоретических исследований физических процессов в системе, логического анализа, идентификации по данным нормальной эксплуатации. Выбираются компоненты вектора управления, параметры системы и возмущения; устанавливаются фазовые координаты; определяется пространство состояния объекта [2, 8]. При разработке оптимальных систем указываются ограничения на компоненты вектора управления и фазовые координаты. Так, ограничения на фазовые координаты определяют принадлежность вектора состояния некоторому замкнутому множеству точек n-мерного пространства (определяют свойства материала). Указываются начальные и краевые условия, осуществляется выбор критерия для оценки качества управления. Модельные исследования являются исходной информацией для уточнения технической задачи, и итерационный процесс может повторяться до достижения заданной точности.
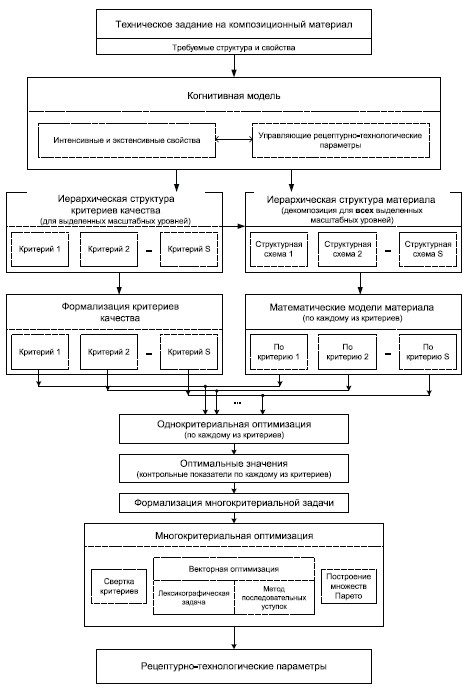
Рис. 1
Как видим, при проектировании композитов как сложных многоцелевых систем возникают проблемы скаляризации нескольких показателей качества; определения иерархической структуры множества критериев с расстановкой приоритетов; области достижимости, построения множества Парето и т.д. [3, 4, 7].
Не останавливаясь на всем комплексе затронутых вопросов, ограничимся использованием принципа Парето (сформулирован Джураном; состоит в предположении, что большая часть результатов вызывается относительно небольшим числом причин). В основном принцип Парето используется для анализа по специально построенным диаграммам возможных источников брака с целью последующего совершенствования технологии производства. Применительно к технологии по принципу Парето «80 % потерь из-за брака или переделок проистекает вследствие 20 % причин». Точно так же Парето обнаружил, что 80 % благосостояния контролируется 20 % людей. И вообще, в количественной формулировке 80 % всех возникающих проблем происходит из-за 20 % исходных материалов, уровня подготовки операторов, работы машин и т.д.
Принцип Парето наглядно характеризует взаимоотношения «причины – результаты» в системе и является одним из наиболее используемых инструментов принятия решений.
Ниже приводится пример использования диаграмм и принципа Парето для управления качеством по виду кинетических процессов формирования требуемых структуры и свойств эпоксидных композитов (ЭК) повышенной плотности для защиты от радиации с использованием отходов стекольной промышленности. По Парето начальные 20 % определяют последующие 80 % времени выхода контролируемого параметра на эксплуатационное значение.
При скалярном управлении y(t) часто оптимизация осуществляется на основе функционала
.
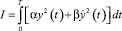В частном случае при α = 1, β = 0
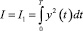
и оптимизация обеспечивает перевод объекта из начального в конечное состояние на промежутке [0, Т] с минимальной энергией управления.
Учитывая, что управление структурой и свойствами материала осуществляется изменением соответствующих рецептурно-технологических параметров, естественен подход к синтезу материалов как к задаче управления [10, 11]. Воспользуемся этой аналогией при синтезе материалов.
Обычно структура композита в большей степени зависит от скорости расхода энергии, чем от ее величины, сообщенной системе. В связи с этим наряду с I1 рассмотрим функционал
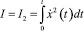
и кумулятивную кривую I2(t). Как оказалось, для всех основных кинетических процессов x(t), t ∈ [0, Т] выполняется условие
I(0,2T) ≥ 0,8 I(T),
что подтверждает возможность использования принципа Парето при оценке формирования физико-механических характеристик материалов. А именно, структура и свойства материала на 80 % определяются начальными 20 % длительности выхода контролируемого параметра на эксплуатационное значение.
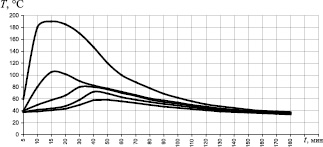
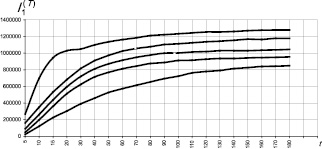
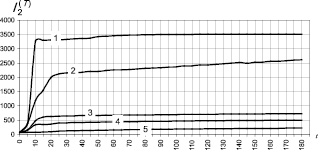
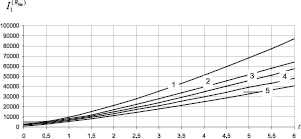
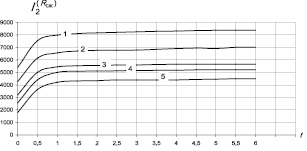
На рис. 2, 3 приводятся кинетические процессы x(t) и соответствующие им кумулятивные кривые тепловыделения и набора прочности для указанных ЭК. Отметим также, что из сравнения кумулятивных кривых I1(t) и I2(t) следует, что при использовании диаграмм Парето необходимо исходить из функционала I2.
Как подтвердили многочисленные исследования, применение принципа Парето значительно облегчает и разработку рецептуры (содержание ингредиентов, гранулометрический состав и т.д.): позволяет выделить элементы в рецептуре, определяющие в основном эксплуатационные характеристики материала. Для рассматриваемых ЭК прочность и плотность в основном определяются степенью наполнения и видом модификатора.
Принцип Парето можно использовать и для итеративного способа улучшения качества материала на основе последовательного построения на каждом этапе соответствующих диаграмм Парето.
a
б
в
Рис. 2. Зависимость температуры саморазогрева при полимеризации эпоксидного композита,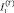 
и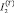 
от t, мин: 1 – ненаполненная смола; 2 – П/Н = 1/5; 3 – П/Н = 1/10; 4 – П/Н = 1/15; 5 – П/Н = 1/20
На основе предложенного подхода к синтезу материалов как к задаче управления осуществлялась разработка эпоксидного композиционного материала, обладающего повышенными защитными свойствами от воздействия ионизирующих излучений. Оптимизация структуры и свойств материала производилась на основе выбора параметров кинетических процессов формирования его физико-механических характеристик (радиационной стойкости, набора прочности, тепловыделения, усадки и др.), описывающихся обыкновенными дифференциальными уравнениями [5].
a
б
в
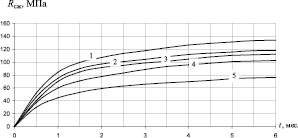
Рис. 3. Зависимость Rсж,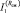 
и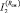 
от t, мес.: 1 – П/Н = 1/15; 2 – П/Н = 1/10; 3 – П/Н = 1/10 и ММ; 4 – П/Н = 1/20; 5 – П/Н = 1/5
Рецензенты:
Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и технологии строительного производства», Пензенский государственный университет архитектуры и строительства, г. Пенза;
Кошев А.Н., д.х.н., профессор кафедры «Информационно-вычислительные системы», Пензенский государственный университет архитектуры и строительства, г. Пенза.
Работа поступила в редакцию 05.08.2014.