В настоящее время известны следующие формы ударных инструментов: клин (двусторонний), долото, конус (пика), плоская сфера. Наиболее эффективной по энергоемкости и износостойкости при разрушении горных пород, особенно крепких (крепость по шкале М.М. Протодьяконова 10 и выше), является сферическая форма [4, 2, 7]. Рабочий инструмент такой формы имеет достаточно высокий коэффициент передачи энергии негабариту.
С другой стороны, многие исследователи [1] отмечают, что наиболее эффективным по энергоемкости при направленном расколе негабаритных кусков горной породы является инструмент клиновидной или долотообразной формы. Однако этот инструмент имеет относительно большую интенсивность износа и, соответственно, невысокий ресурс.
Можно предположить, что еще более эффективной как по энергоемкости и износостойкости инструмента, так и по направленности удара и управления процессом разрушения может стать форма инструмента, контактная поверхность которого будет эллиптической формы, то есть некоторой промежуточной формой между клиновидной и сферической формой ударных инструментов. Следует отметить, что расчетов на статическую и усталостную прочность рабочего инструмента эллиптической формы в известной литературе нет.
Практика эксплуатации различных по форме рабочих инструментов показывает, что потеря работоспособности происходит из-за относительно больших контактных напряжений, которые возникают на площадке контакта его с горной породой. При превышении этими напряжениями предела текучести, выносливости или прочности может произойти питтинг, расклепывание, а также износ поверхности контакта.
В основе расчетов на контактную прочность лежит формула Герца [3, 5, 10]. Она достаточно точно определяет контактные напряжения при взаимодействии тел с постоянными радиусами кривизны:
σн = А[РЕ2ρ-2]0,333 (1)
где ρ – приведенный радиус кривизны рабочего инструмента, м;
Е – приведенный модуль упругости материала рабочего инструмента и горной породы, Па;
Р – усилие прижатия тел, Н;
А – постоянный коэффициент пропорциональности.
Формула 1 применима для расчета контактных напряжений при взаимодействии: шар-шар; цилиндр-шар; цилиндр-цилиндр(оси цилиндров перпендикулярны); шар-плоскость.
Модуль упругости горной породы является случайной величиной [2], имеющей коэффициент вариации до 30 %. Для предлагаемого рабочего инструмента радиусы кривизны в двух взаимно перпендикулярных плоскостях не равны друг другу. Следовательно, осуществить точное решение уравнения Герца и аналитически определить контактные напряжения с необходимой степенью точности затруднительно. В данной работе предложено приближенное решение данной проблемы, основанное на законе сохранения энергии.
Согласно этому закону определим площадь контакта рабочего инструмента с ровной поверхностью куска горной породы. Объем эллипсоида контактных давлений (2πabσНmax /3) равен силе давления (Р) [10]:
σНmax = 1,5*Р/πab, (2)
где a и b – полуоси эллипса площадки контакта рабочего инструмента с горизонтальной плоскостью, м (см. рис. 1).
На рис. 1 приведено сечение рабочего инструмента в двух плоскостях: ОА = R; ОА1 = r.
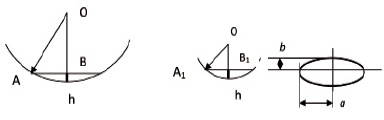
Рис. 1. Зависимость площади контакта при действии постоянной единичной силы от соотношения радиусов ударной части: 1 ряд – по теории Герца; 2 ряд – по методу конечных элементов
Площадка контакта рабочего инструмента в проекции на горизонтальную плоскость имеет форму эллипса с полуосями: АВ = a и А1В1 = b. Из прямоугольных треугольников ОАВ и ОА1В1 можно определить a, b и, соответственно, площадь эллипса.
Fэ = π a*b = π [4Rrh2 -2(R+r)h3 +h4]0,5, (3)
где h – величина заглубления рабочего инструмента, м.
Так как величина заглубления рабочего инструмента в горную породу на два-три порядка меньше радиусов, то вторым и третьим членом уравнения 3 можно пренебречь и его можно преобразовать к виду:
Fэ ≈ 2 π h(Rr) 0,5 (4)
Из формулы Герца следует [3,5,10], что радиус площадки при контакте шара с плоскостью равен:
a = А[РЕ-1 ρ]0,333 (5)
С другой стороны, согласно рис. 1, этот радиус равен:
a = [R2 -(R- h)2]0,5 (6)
Учитывая соотношение радиуса и величины заглубления, уравнение 5 можно преобразовать к виду:
a ≈ (2Rh)0,5 (7)
Определим величину заглубления из уравнения 7 и подставим её в уравнение 4. После преобразований получим:
h = (2R)-1А2[Р2Е-2ρ2]0,333 (8)
В работе [3] приведена формула Герца для определения сближения ( в нашем случае заглубления) при статическом сжатии двух тел:
h = kР 2/3 (9)
где k – коэффициент пропорциональности.
Приравняв уравнения 7 и 8, получим величину коэффициента пропорциональности:
k = (2)-1А2[Е-2ρ-1]0,333 (10)
Используя уравнение, приведенное в [10], а также уравнения 4 и 10, получим зависимость величины площади контакта рабочего инструмента эллиптической формы:
Fэ = 3,76(Rr)0,5[Р2Е-2r-1]0,333 (11)
Если подставить в уравнение 10 R = r, что соответствует контакту сферы с плоскостью, то получится уравнение
Fсф = 3,76[Р2Е-2r2]0,333 (12)
Это уравнение получится, если решить совместно уравнения 2.27...2.29, приведенные в [6]. Это подтверждает известный факт, что сфера является частным случаем эллипсоида.
Используя результаты работы [5] и формулу 11, получим уравнение для определения максимальных контактных напряжений в эллипсоиде:
σНmax = 0,4(Rr)-0,5(РЕ2r)0,333 (13)
Если подставить в уравнение 11 R = r, что соответствует контакту сферы с плоскостью, то получится известное [5] уравнение
σНmax.сф = 0,4(РЕ2r-2)0,333 (14)
Таким образом, уравнение 13 не противоречит теории Герца и позволяет определять контактные напряжения в эллипсоиде, а затем сравнить их с допускаемыми и сделать вывод о работоспособности или неработоспособности рабочего инструмента.
Осуществить экспериментальным методом проверку адекватности формул 11 и 13 практически невозможно. Это объясняется тем, что использовать тензометрию для замера контактных напряжений невозможно из-за относительно больших размеров тензодатчика. Минимальная длина активной части проволочных или фольговых тензодатчиков равна 5 мм. Последний будет замерять средние по его длине напряжения, что существенно искажает общую картину распределения напряжений. Кроме того, установка тензодатчиков предполагает подготовку площадки, что существенно изменяет форму рабочей части инструмента.
Наиболее целесообразным и экономичным при проверке адекватности моделей будет апробированный метод конечных элементов [6, 8, 9].
На рис. 2 приведен график изменения площади эллиптической площадки контакта при действии на ударник постоянной единичной силы. Зависимость имеет нелинейный характер и показывает, что уменьшение радиуса кривизны одной из осей с 220 мм до 22 мм приводит к существенному уменьшению площади контакта при статическом нагружении, что не противоречит классической теории контактного взаимодействия.
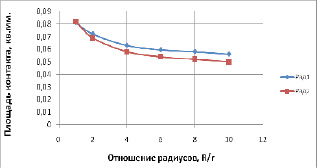
Рис. 2. Зависимость площади контакта при действии постоянной единичной силы от соотношения радиусов ударной части: 1 ряд – по теории Герца; 2 ряд – по методу конечных элементов
На рис. 3 приведена зависимость величины максимальных контактных напряжений в зависимости от размеров ударной части при действии постоянной силы такой величины, которая для наиболее «острого» ударника обеспечивает максимальные контактные напряжения, равные пределу прочности разрушаемого материала (200 МПа).
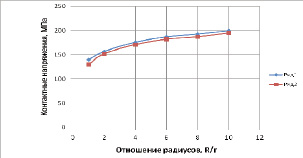
Рис. 3. Зависимость величины максимальных контактных напряжений (МПа) от размеров ударной части при постоянной силе взаимодействия 1 ряд – по теории Герца; 2 ряд – по методу конечных элементов
Из рис. 2 и рис. 3 видно, что размеры площадей контакта рабочей части инструмента, а также контактные напряжения, определенные по теории Герца и методу конечных элементов имеют отличие не более 12 %. Такое отличие приемлемо для инженерных расчетов.
Выводы
На основании теории Герца определена зависимость контактных напряжений в рабочем инструменте, имеющем различные радиусы кривизны в рабочей части. Адекватность формулы для определения контактных напряжений подтверждена с помощью метода конечных элементов. Расхождение результатов не превышает 12 %.
В результате численного решения задачи теории упругости о контактном взаимодействии стальной эллипсоидной ударной части инструмента с плоской гранью параллелепипеда, имитирующего негабарит, установлено, что отношение размера большой оси к размеру малой оси должно составлять 3,5.
Наибольший уровень напряжений, не превышающий 200 МПа, локализуется в зоне ударного взаимодействия инструмента и негабарита. В остальной части инструмента напряжения существенно ниже.
Рецензенты:
Неволин Д.Г., д.т.н., заведующий кафедрой «Проектирование и эксплуатация автомобилей», ФГБОУ ВПО «Уральский государственный университет путей сообщения», г. Екатеринбург;
Мальцев В.А., д.т.н., доцент, директор института материаловедения и металлургии, ФГАОУ ВПО им. первого Президента РФ Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 24.06.2014.



