В настоящее время при планировании развития производства в сфере сервиса и других областях человеческой деятельности часто возникает необходимость в решении задач оптимального распределения и размещения ресурсов [5–8]. Необходимость распределения ограниченных ресурсов между параллельными объектами возникает очень часто. Однако оптимальное распределение ресурсов зачастую связано со значительными вычислительными трудностями. Причина в том, что параллельные агрегаты обычно являются однотипными. А это приводит к тому, что базисная матрица системы ограничений задачи распределения ресурсов между ними оказывается близкой к вырожденной и приводит к неустойчивости решения [1].
Проблемы отыскания приближенных решений систем алгебраических уравнений с вырожденной базисной матрицей рассматривались академиком А.Н. Тихоновым [2]. Его идеи получили распространение и для решения оптимизационных задач с матрицей системы ограничений, близкой к вырожденной. Так, профессор А.А. Первозванский предложил метод, который он назвал «методом возмущений в конечномерных оптимизационных задачах» [1]. Суть его состоит в выделении порождающей системы, полученной из исходной оптимизационной задачи без учета слабых различий между ее ограничениями, т.е. без возмущений, и в использовании характеристик порождающей системы для оценки роли возмущений в формировании оптимального решения. Такой подход имеет большую теоретическую значимость, однако его вычислительная процедура связано с достаточна жесткими ограничениями на характер вырожденности и дает только приближенное решение.
В предыдущих работах авторов предложен метод расширения множества допустимых значений для решения оптимизационных задач распределения и размещения ресурсов между параллельными объектами с учетом возможной, но не обязательной вырожденности матриц ограничений. В этой работе метод расширения обобщен для решения задач имитационного анализа и улучшения найденных ранее оптимальных режимов распределения ресурсов в параллельных системах, характеризуемых нестационарностью ряда параметров.
Постановка задачи
Рассмотрим модель задачи распределения ресурсов (ЗРР) между параллельными объектами в ее линейной постановке:
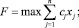 (1)
(1)
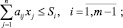 (2)
(2)
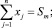 (3)
(3)
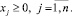 (4)
(4)
В соответствии с аппаратом метода расширения, где 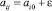 , введем вспомогательную расширенную задачу, полученную из исходной (1)–(4) путем отбрасывания ограничений вида (2):
, введем вспомогательную расширенную задачу, полученную из исходной (1)–(4) путем отбрасывания ограничений вида (2):
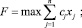 (5)
(5)
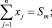 (6)
(6)
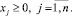 (7)
(7)
Необходимо установить связь между решениями исходной (1)–(4) и расширенной (5)–(7) задач и тем самым свести решение достаточно сложной задачи к решению простой расширенной задачи. Значение целевой функции (5) расширенной задачи в ее оптимальной точке является предельно возможным значением целевой функции (1) исходной задачи, так как допустимое множество решений Х исходной задачи является подмножеством множества допустимых решений XP расширенной задачи X ⊆ XP. Поэтому любой переход от точки xp∈XP к другой точке x ∈ X будет ухудшать значение целевой функции или, другими словами, этот переход будет означать спуск от FP к другому значению целевой функции.
Приведем общую структуру решения задачи распределения ресурсов методом расширения:
- решение расширенной задачи;
- проверка полученного решения на допустимость по ограничениям (4) исходной задачи, и если решение допустимо, то оно оптимально;
- выбор направления и шага спуска;
- переход к новому решению.
Новое решение, полученное в результате спуска будет, очевидно, оптимальным, если спуск в выбранном направлении приводит к наименьшему изменению значения целевой функции по сравнению с другими направлениями.
Предположим, что правые части ограничения (2) – ресурсы Si, где 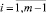 , в течение некоторого интервала времени могут целенаправленно изменяться на некоторую величину ΔSi, где
, в течение некоторого интервала времени могут целенаправленно изменяться на некоторую величину ΔSi, где 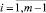 . При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используют теневые цены [3]. Заметим, что теневая цена – это термин, который экономисты используют при характеристике ценности ресурсов. Теневая цена (ценность ресурса) характеризует интенсивность улучшения оптимального значения F.
. При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используют теневые цены [3]. Заметим, что теневая цена – это термин, который экономисты используют при характеристике ценности ресурсов. Теневая цена (ценность ресурса) характеризует интенсивность улучшения оптимального значения F.
Структура модели задачи (1)–(4) позволяет провести следующие аналитические выкладки [4]. При имитационном поиске области изменения параметров исходной модели с целью улучшения найденных ранее оптимальных решений задачи распределения ресурсов необходимо при моделировании значений ΔS учитывать неравенство для каждой эффективной составляющей S:
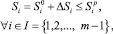 (8)
(8)
где Sp – значения правых частей ограничений (2), соответствующие решению хр, хр – оптимальное решение расширенной задачи (5)–(7) [4], где 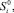
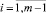 – значения правых частей ограничений, соответствующие оптимальному решению исходной задачи.
– значения правых частей ограничений, соответствующие оптимальному решению исходной задачи.
Специфика математической модели задачи распределения ресурсов позволяет не только найти оптимальное значение дефицитного ресурса, но и установить взаимное влияние между собой нескольких дефицитных ресурсов. Как показывает опыт решения оптимальных задач, на практике эффективными оказываются не все ограничения вида (2). Для двух эффективных ограничений с соответствующими ресурсами 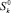 и
и 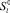 справедливо следующее утверждение: «Наибольший эффект от изменения ресурсов будет достигнут, если в новом решении ограничения, эффективные прежде, будут также эффективны».
справедливо следующее утверждение: «Наибольший эффект от изменения ресурсов будет достигнут, если в новом решении ограничения, эффективные прежде, будут также эффективны».
Формула 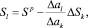 при заданном изменении основного ресурса (DSk) позволяет найти новые значения ресурсов, для которых все ограничения, эффективные в прошлом, также останутся эффективными.
при заданном изменении основного ресурса (DSk) позволяет найти новые значения ресурсов, для которых все ограничения, эффективные в прошлом, также останутся эффективными.
Наряду с увеличением возможно и уменьшение некоторых видов ресурсов. Очевидно, что любое изменение в меньшую сторону ресурса S влечет неизбежное ухудшение значения целевой функции.
Напомним, что для решения задач данного класса был разработан метод расширения [9–10], предполагающий решение ЗРР путем направленного перехода к ее оптимальному решению из точки, соответствующей решению более простой задачи (5)–(7) с расширенной областью допустимых решений.
x = xр + h;
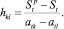
При этом оптимальным является направление (k, l), минимизирующее выражение
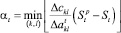 (9)
(9)
по всем возможным направлениям спуска. Величина шага спуска 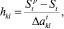 найденная из условия (9), обеспечивает минимальное отклонение F(x) от F(xp), но гарантирует выполнение только ограничения с индексом t. Чтобы не было нарушено ни одно из ограничений, выбирается такое направление, которому соответствует наибольшее из выражений (10) по всем t ∈ IH, где IH – множество индексов ограничений (2), которые были нарушены при подстановке в них хр, т.е.
найденная из условия (9), обеспечивает минимальное отклонение F(x) от F(xp), но гарантирует выполнение только ограничения с индексом t. Чтобы не было нарушено ни одно из ограничений, выбирается такое направление, которому соответствует наибольшее из выражений (10) по всем t ∈ IH, где IH – множество индексов ограничений (2), которые были нарушены при подстановке в них хр, т.е.
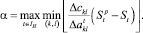 (10).
(10).
Использование имитационной модели для анализа и оптимизации распределения и размещения ресурсов
Общая структура имитационной модели для обеспечения стабильности системы и улучшения найденных ранее оптимальных режимов должна обеспечить выполнение следующих основных элементов:
а) решение задачи распределения ресурсов;
б) моделирование возможных изменений параметров модели оптимизационной задачи;
в) определение области изменения нестационарных параметров модели, обеспечивающей устойчивость полученных ранее режимов либо приводящая к улучшению оптимального решения задачи.
Учитывая важность правильного распределения и эффективного использования материальных ресурсов, а также необходимость постоянного учета и контроля их распределения, на предприятиях целесообразно применять эффективные информационные системы каждодневного учета товарных запасов и движения ресурсов. Представленная имитационная модель используется при разработке такой информационной системы. Основные подсистемы информационно-имитационной системы распределения и размещения ресурсов и объектов приведены на рисунке.
Целью разработки информационно-имитационной системы является оптимальное распределение и размещение ресурсов в условиях, наиболее приближенных к реальным, т.е. с учетом стохастического характера нестационарных параметров решаемой задачи. Имитационная модель анализа параметров должна обеспечить реализацию следующих взаимосвязанных задач: идентификацию законов распределения нестационарных параметров; имитацию возможного изменения нестационарных параметров; решение задачи распределения и размещения ресурсов; определение области устойчивости полученных решений; обработка результатов и анализ эффективности распределения и размещения ресурсов.
Для разработки информационно-имитационной системы распределения и размещения ресурсов и объектов выбран современный аппарат теории имитационного моделирования, который позволяет моделировать все классы случайных закономерностей, включая сложные зависимые и независимые случайные события, непрерывные, дискретные и многомерные случайные величины и параметры, стационарные, нестационарные и марковские случайные процессы, а также все виды ординарных и неординарных случайных потоков. Также он позволяет исследовать сложные экономические системы, когда невозможно получить знания о них или прогнозировать их поведение из-за сложности или отсутствия полной теории. Теория имитационного моделирования как метод научного познания, анализа и прогнозирования поведения экономических объектов особенно эффективна, когда проводить на практике эксперименты с объектом весьма рискованно или невозможно.
Подсистема «Закономерности случайных экономических параметров». Исходным материалом для выявления закономерностей pаспpеделения являются экспериментальные данные, полученные в результате большого числа наблюдений и образующие выборку заданного объема. В данной системе предусмотрены идентификация числовых характеристик выборки, а именно: среднее арифметическое (с помощью которого идентифицируется математическое ожидание), выборочная дисперсия (для идентификации дисперсии), выборочный коэффициент корреляции (для идентификации коэффициентов корреляции между парой случайных величин) и идентификация функций плотности непрерывных и дискретных случайных величин. Для статистической оценки гипотезы о том, что совокупность эмпирических данных незначительно отличается от той, которую можно ожидать при выбранном теоретическом законе pаспpеделения, чаще всего используются кpитеpии согласия Пирсона, Колмогоpова – Смиpнова, Мизеса.
Подсистема «Имитация процессов поступлений ресурсов» имитирует поступление случайных стационарных и нестационарных потоков ресурсов и потоков ресурсов со случайными величинами.
Подсистема «Оптимизация распределения и размещения ресурсов и объектов» оптимизирует линейные задачи распределения, нелинейные задачи распределения, распределение с различными приоритетами и задачи размещения.
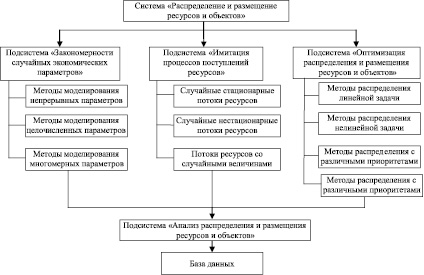
Структура системы «Распределения и размещения ресурсов и объектов»
Подсистема «Анализ распределения и размещения ресурсов и объектов» анализирует влияние измененных параметров на полученное решение.
Заключение
Научные результаты применимы при создании информационных систем для предприятий различных отраслей и для научных и проектных организаций для распределения и размещения ресурсов и объектов. Предполагается развитие предложенного в работе метода расширения области допустимых значений для решения дискретных, нелинейных и многоуровневых задач распределения и размещения ресурсов и объектов.
Рецензенты:
Бияшев Р.Г., д.т.н., профессор, зам. директора по прикладным, рисковым и инициативным проектам, заведующий лабораторией информационной безопасности, г. Алматы;
Утепбергенов И.Т., д.т.н., профессор кафедры «Инженерная кибернетика» Алматинского университета энергетики и связи, г. Алматы.
Работа поступила в редакцию 04.06.2014.



