Повышение эффективности транспортно-переместительных операций до сих пор является приоритетной задачей для лесопромышленного комплекса в целом и лесозаготовительных предприятий в частности. Это обусловлено в первую очередь тем, что транспортные расходы на освоение лесного фонда могут достигать значительных величин в общем объеме лесозаготовительных работ. В русле этих тенденций в Петрозаводском государственном университете на протяжении значительного времени проводятся исследования, направленные на повышение эффективности транспортно-переместительных операций [7, 8, 10, 11, 12, 13, 14] с использованием функционально-технологического анализа. Одним из направлений этих исследований стала работа по совершенствованию методов тяговых расчетов, разработке алгоритмов и программ для моделирования движения лесовозных автопоездов и определению показателей движения в конкретных условиях эксплуатации.
До настоящего времени тяговые расчеты для определения допустимой нагрузки, скорости движения, производительности автопоездов выполняются традиционными способами, основанными на методе равновесных скоростей. Эти способы уточнялись и применялись при проектировании лесовозных дорог и организации лесотранспортных работ рядом известных ученых и исследователей [1, 2, 3, 4, 5, 6]. Однако на современном этапе традиционные методы расчетов не удовлетворяют возросшим требованиям ввиду того, что не учитывают многие факторы, влияющие на показатели движения. Проведенные исследования показали, что графики движения, рассчитанные по методу равновесных скоростей, не адекватны фактическим. Результаты расчетов не обеспечивают достаточной точности, в частности расхождение по времени движения по всему маршруту составляет 40–45 % в сравнении с фактическими данными, а на отдельных участках данные отличаются вдвое [7, 8, 10, 11, 12, 13, 14].
На практике лесовозные дороги характеризуются сложной структурой и функциональной применимостью. Функционально-технологические ограничения скорости движения имеют место на крутых поворотах по условиям устойчивости движения с учетом центробежной силы, на переломах продольного профиля с учетом допустимой перегрузки рессор, на вертикальных кривых по допускаемому центростремительному ускорению; по условиям видимости на вертикальных выпуклых кривых, на крутых поворотах в закрытой местности; по состоянию покрытия на определенных участках дороги, а также ограничения, устанавливаемые директивно, например, при движении в населенных пунктах, пересечении дорог и т.д.
При подходе к таким участкам и их преодолении необходимо снизить скорость до величины ограничения. На практике водители лесовозных автопоездов определяют режимы движения и интенсивность снижения скорости, руководствуясь опытом. При расчете скоростей движения при моделировании движения лесовозных автопоездов для решения этой задачи приходилось проводить многочисленные расчеты [12, 13, 14] через короткие интервалы, с тем, чтобы при подходе автопоезда к участкам ограничения его скорость не превышала допустимую и не снизилась ниже νогр в значительных пределах. Поэтому при расчетах очень важно определить расстояние от начала расчетного участка до точки, с которой следует переходить к снижению скорости в различных режимах (с торможением колесными тормозами, моторным тормозом, торможение двигателем).
Для определения расстояния до точки, начиная с которой необходимо прекратить разгон автопоезда и перейти к режиму торможения, в качестве исходной используется зависимость при движении автопоезда на вертикальной кривой [9]:
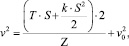(1)
где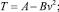 
; 
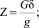
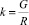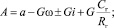
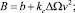; ν0 – скорость движения в начале участка, м/с; ν – скорость движения автопоезда в конце участка, м/с; S – длина расчетного участка, м; G – вес автопоезда, кгс; Rг – радиус горизонтальной кривой; Сг – коэффициент, учитывающий увеличение сопротивления движению на горизонтальных кривых; R – радиус вертикальной кривой (при расчете показателей движения на вертикальных выпуклых кривых применяется со знаком «+», на вогнутой кривой со знаком «–»); а и b – коэффициенты зависимости, аппроксимирующей тяговую или тормозную характеристику автопоезда в виде F = a – bν2; ω – коэффициент сопротивления качению; δ – коэффициент учета инерции вращающихся масс; kс, Δ, Ω – соответственно коэффициент сопротивления воздушной среды для автомобиля, коэффициент, учитывающий дополнительное сопротивление от прицепов; лобовая площадь автомобиля, м2; i – продольный уклон; g – ускорение силы тяжести, м/с2.
К точке начала торможения расчетная скорость движения достигается автопоездом в режиме разгона и равна скорости, начиная с которой необходимо начать торможение с тем, чтобы к началу участка, имеющего ограничение скорости, скорость движения автопоезда снизилась до νогр.
При этом при длине элемента продольного профиля S скорость движения в режиме разгона определяется на расстоянии s – sт, где Sт – длина участка торможения.
Следовательно, для определения sт и (s – sт), а также величины скорости, с достижением которой в режиме разгона необходимо начать торможение, нужно решить систему двух уравнений, первым из которых определяется значение скорости в точке начала торможения при разгоне автопоезда, а вторым – скорости при торможении автопоезда до снижения скорости в конце участка до νогр.
В режиме разгона:
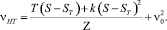(2)
В режиме торможения:
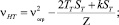(3)
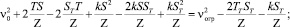
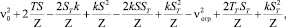(4)
где S – длина участка, м; ST – расстояние, на котором производится торможение, м;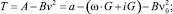 
Т и ТТ значения функционала 
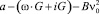соответственно для режима разгона и торможения.
Обозначив
,
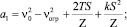
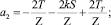
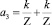получаем квадратное уравнение вида
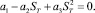
Решение квадратного уравнения:
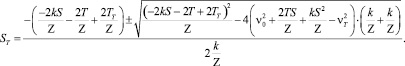(5)
В качестве примера определим расстояние от начала участка, на котором с режима разгона необходимо перейти на режим торможения моторным тормозом. Автопоезд МАЗ-6303-26 + МАЗ-83781 начинает движение на участке вертикальной кривой радиусом 10000 м с начальным уклоном 0,00 длиной 200 м с начальной скоростью 11,5 м/с, на 7-й передаче, ω = 0,02; на следующем участке по условиям видимости ограничение составляет 11 м/с. В работе [12, 13] приведены коэффициенты зависимостей, аппроксимирующих тяговую и тормозную характеристики: а = 1480; В = 1,41; аТ = –1459; ВТ = 2,64. В результате расчетов получим Sт = 70, 27 м.
Для проверки точности расчетов по формуле (1) определим скорость движения, которой достигает автопоезд на расстоянии S – ST (200 – 70,27 м) = 129,73 м перед началом торможения и значение скорости, с которой автопоезд начнет движение на участке ограничения.
В конце участка разгона:
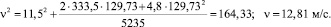
В начале участка ограничения:
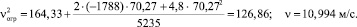
Таким образом, доказана правомерность предложенного метода расчетов и достаточная точность расчетов.
На прямолинейных в профиле участках определение точки начала торможения упрощается. При разгоне скорость движения определяется по формуле
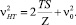(6)
При торможении:
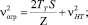
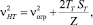(7)
где ST – расстояние, которое пройдет автопоезд в режиме торможения до достижения скорости νогр (м/с), м.
Таким образом
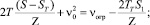
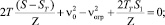
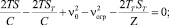
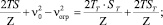
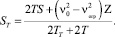(8)
Правомерность предложенных зависимостей подтверждается следующим примером. Автопоезд МАЗ-6303-26 + МАЗ-83781 начинает движение на участке с уклоном – 0,010 и длиной 200 м с начальной скоростью 11,5 м/с, ω = 0,02 на следующем участке ограничения скорости составляет 11 м/с. Определить расстояние от начала участка до точки, начиная с которой
А = 1480 – 48000∙0,01 = 1000;
Т = 1000 – 1,41∙11,5 = 813,5;
А1 = –499 – 48000∙0,01 = –979;
ТТ = –979 – 2,64∙112 = –1298;
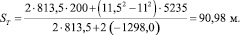
Скорость движения в конце участка разгона определяется по формуле (7), при этом
Sкр = S – ST = 200 – 90,98;
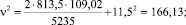ν = 12,9 м/с;
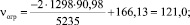ν = 11 м/с.
Выведенные зависимости и предложенная методика расчетов позволяют определить скорость неустановившегося движения лесовозных автопоездов с учетом ограничений скорости, а также выбрать оптимальное чередование режимов движения, ускорить и уточнить тяговые эксплуатационные расчеты.
Рецензенты:
Григорьев И.В., д.т.н., профессор, заведующий кафедрой технологии лесозаготовительных производств, ФГБОУ ВПО «Санкт-Петербургский государственный лесотехнический университет имени С.М. Кирова», г. Санкт-Петербург;
Питухин А.В., д.т.н., профессор, декан лесоинженерного факультета ПетрГУ, ФГБОУ ВПО «Петрозаводский государственный университет», г. Петрозаводск.
Работа поступила в редакцию 04.06.2014.