С развитием сетевых технологий развиваются и сетевые угрозы. В последнее время все большую актуальность приобретают DDoS-атаки. DoS-атака (атака типа «отказ в обслуживании», от англ. Denial of Service) – атака на вычислительную систему с целью довести её до отказа, то есть создание таких условий, при которых легальные пользователи системы не могут получить доступ к предоставляемым системным ресурсам (серверам), либо этот доступ значительно затруднён. Распределенная атака DoS (distributed DoS, DDoS) проводится одновременно через множество устройств [7].
Для противодействия DDoS-атакам применяется целый ряд механизмов, особой значимостью обладают средства обнаружения вторжений. Ведь своевременное обнаружение DDoS-атаки позволит сохранить работоспособность сети, так как если не остановить у провайдера трафик, предназначенный для переполнения атакуемой сети, то сделать это на входе окажется невозможным, поскольку вся полоса пропускания будет уже занята. Стандартные методы анализа статистики не позволяют выявлять неизвестные ранее атаки, поэтому в качестве механизма решения данной проблемы активно выступают нейронные сети.
Искусственная нейронная сеть (ИНС) – математическая модель, а также её программная или аппаратная реализация, построенная по принципу организации и функционирования биологических нейронных сетей – сетей нервных клеток живого организма [2, 3]. ИНС используются практически во всех средствах обнаружения вторжений как отдельно, так и в комплексе с другими механизмами защиты.
Целью исследования является анализ мер противодействия и совершенствование механизма защиты от DDoS-атак в виде средства обнаружения вторжений на основе искусственных нейронных сетей, результаты которой возможно применить в уже существующих системах защиты. В данной работе отражены результаты исследований, настройки и применения метода роя частиц при оптимизации параметров нейронной сети для эффективного обнаружения DDoS-атак.
Материалы и методы исследования
В работе использовалась модель многослойного персептрона с двумя скрытыми слоями, построенная на сигмоидальной логистической функции активации. Количество входных сигналов – 28. В скрытых слоях количество нейронов составляет 28 и 14, в выходном слое содержится 2 нейрона. Представленная модель выдает ответы (1, 0) и (0, 1), характеризующие наличие или отсутствие атаки.
Для анализа эффективности обучения сети была выбрана база данных, составленная одним из ведущих университетов [9], содержащая в себе сведения об атаках различных типов, однако в рассматриваемой работе использовались лишь те параметры, которые отвечают за атаки типа DoS.
В настоящее время при оптимизации параметров сложных систем [5] все чаще применяются природные механизмы поиска; в последние годы интенсивно разрабатывается научное направление «Роевой интеллект» (Swarm intelligence), включающее в себя целый ряд эвристических алгоритмов. Для исследования эффективности работы указанных алгоритмов был разработан программный комплекс, на основе которого проведен сравнительный анализ [4]. Так как достаточно высокую скорость и точность вычислений показал метод роя частиц, для оптимизации параметров нейронной сети был выбран именно он.
Метод роя частиц (МРЧ), particle swarm optimization (PSO) – эвристический метод оптимизации, использующий имитацию социального поведения роя некоторых элементов (птиц, рыб, светлячков, пчел и т.д.), применение которого не требует знания точного градиента оптимизируемой функции.
В алгоритме агентами являются частицы, которые в каждый момент времени имеют в пространстве параметров задачи некоторое положение и скорость. Правила, по которым частица меняет свое положение и скорость, определяются на основе вычисления целевой функции частицы. Канонический метод роя частиц был предложен в 1995 г. в работе J. Kennedy, R. Eberhart [6], в основе которого лежит следующий принцип: на каждой итерации для определения следующего положения частицы учитывается информация о наилучшей единице от «соседей» и информация о данной частице на том шаге, когда ей соответствовало оптимальное значение целевой функции. Существуют модификации канонической модели, учитывающие значения целевых функций всех частиц роя, в некоторых моделях частицы группируются в несколько роев и т.д. [1].
В классическом варианте алгоритма скорость каждой частицы в рое изменяется по следующей формуле:
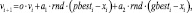 (1)
(1)
где vi – скорость частицы в момент времени i; xi – координата частицы в момент времени i; o – весовая доля инерции; a1, a2 – некоторые константы; rnd – случайное значение в промежутке (0; 1]; pbesi, gbesti – локальное и глобальное лучшее положение частицы в момент времени i.
Затем происходит изменение положения каждой из частиц:
x i+1 = v i+1 + xi. (2)
Следует отметить, что значения скорости и координаты представлены в виде векторных значений и содержат множество компонент, а не просто одно скалярное значение. Количество итераций и частиц в рое указывают на продолжительность работы алгоритма, а следовательно, и на качество получаемых результатов; значения констант определяются экспериментально исходя из поставленной задачи.
Процесс обучения нейронной сети представляет собой стандартный метод обратного распространения ошибки, после работы которого синаптические веса дополнительно корректируются. Схема обучения представлена на рисунке.
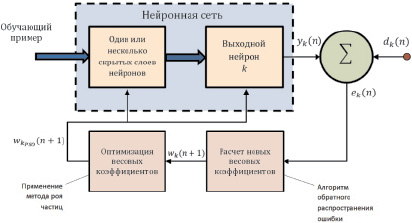
Схема обучения нейронной сети
Синаптические веса каждого нейрона k с помощью метода обратного распространения ошибки рассчитываются по следующей формуле:
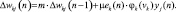 (3)
(3)
Затем синаптические веса дополнительно корректируются методом роя частиц:
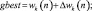 (4)
(4)
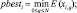 (5)
(5)
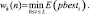 (6)
(6)
Полученный результат метода обратного распространения ошибки записывается в вектор gbest, затем создается рой с количеством частиц L, где L – количество синаптических связей каждого нейрона в слое, а переменная N отображает количество нейронов в рассматриваемом слое. Далее случайно генерируются начальные координаты каждой из частиц и их скорости. После каждой итерации алгоритма в переменную pbesti заносится лучший текущий результат, при котором значение среднеквадратичной ошибки минимально. После N итераций алгоритма оптимальное значение pbesti записывается в вектор синаптических весов wk(n), где n – номер обучающего примера.
Одной из основных задач является правильная настройка параметров метода роя частиц, так как при неправильной настройке метода процесс обучения может вовсе остановиться на хаотичных и слишком больших значениях синаптических весов, при которых, вне зависимости от входных параметров, на выходе получается один и тот же результат. Или же метод роя частиц совсем не окажет никакого воздействия на процесс обучения.
В задаче разработки средства обнаружения вторжений оптимальные начальные значения синаптических весов лежат в промежутке [–0,5; 0,5], поэтому исходные положения частиц целесообразно генерировать в том же диапазоне значений [–0,5; 0,5]. Чтобы частицы не разлетались далеко за пределы установленного промежутка и кардинально не нарушили процесс обучения, необходимо задать им начальные скорости движения в диапазоне [–0,03; 0,03]. Далее в ходе проведенных исследований были экспериментально установлены оптимальные значения констант: a1 = 0,4; a2 = 0,5, а также значение весовой доли инерции: o = 0,5.
Использование корректора необходимо применять только в том случае, если нейронная сеть дает ответ, близкий к желаемому, ведь в противном случае синаптические веса резко изменяются, вызывая еще большую неточность в работе алгоритма обучения. Во избежание смещения синаптических весов в сторону одной из возможных комбинаций значений выходного слоя нейронной сети необходимо подавать обучающие примеры с равновероятным желаемым ответом. В целях повышения эффективности работы алгоритма обучения рекомендуется подавать одновременно несколько примеров со всевозможными комбинациями выходных значений сети.
Результаты исследования и их обсуждение
Таким образом, была достигнута оптимальная настройка параметров метода роя частиц, которая оказывает существенное влияние на ход процесса обучения методом обратного распространения ошибки, постепенно снижая значение среднеквадратичной ошибки всей сети и уменьшая количество ложных срабатываний.
Для исследования эффективности работы предложенной методики был разработан программный модуль, в котором реализована вышеописанная модель нейронной сети, обучающейся по одному из выбранных пользователем методов. Используется одна и та же база для обучения, состоящая из 283891 примеров, а для проверки правильности полученного решения создана вторая база такого же размера, но с совершенно иными примерами входных данных, чтобы иметь возможность проанализировать вероятность обнаружения неизвестных атак. Для анализа точности полученного ответа рассчитывалось значение среднеквадратичной ошибки:
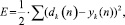 (7)
(7)
где dk(n) – желаемый ответ; yk(n) – полученный ответ.
В ходе сравнительного анализа исследуемых методов обучения (стандартный метод обратного распространения ошибки и метод роя частиц) проведено несколько повторяющихся этапов процесса обучения вновь сгенерированной нейронной сети во избежание ошибок полученных результатов. Усредненные значения среднеквадратичных ошибок занесены в таблицу.
Сравнительный анализ среднеквадратичной ошибки
|
Количество пройденных примеров |
Среднеквадратичная ошибка метода обратного распространения ошибки |
Среднеквадратичная ошибка метода роя частиц |
|
100 |
0,004 |
0,00016 |
|
1000 |
2,65E-05 |
2,79E-05 |
|
5000 |
2,37E-05 |
1,08E-08 |
|
10000 |
8,54E-06 |
2,58E-09 |
|
30000 |
4,98E-06 |
1,11E-13 |
|
60000 |
3,19E-06 |
3,97E-16 |
|
100000 |
1,79E-06 |
6,45E-17 |
|
150000 |
9,61E-07 |
4,02E-20 |
|
250000 |
1,19E-06 |
3,88E-22 |
Из таблицы видно, что при использовании метода роя частиц для коррекции алгоритма обучения значение среднеквадратичной ошибки резко стремится к нулю в отличие от метода обратного распространения ошибки.
Выводы
Разработанная методика применения метода роя частиц в качестве алгоритма обучения нейронной сети не только повышает точность получаемых результатов, но и снижает количество ложных срабатываний. Так, например, сеть, обученная всей базой из 283891 примеров стандартным методом обратного распространения ошибки, выдает 670 ошибок (0,670 %) из 100000 тестовых примеров, тогда как методом роя частиц – 439 ошибок (0,439 %).
Такое незначительное количество ошибок в обоих случаях обусловлено большим размером нейронной сети для задачи обнаружения факта атаки, то есть для вывода результата «да» или «нет». Но для более сложных задач (например, для распознавания вида атаки) с помощью данной методики можно заметно уменьшить количество ложных срабатываний (ошибок), а резкое повышение точности вычислений позволит значительно сократить время обучения.
Рецензенты:
Видовский Л.А., д.т.н., доцент, зав. кафедрой информационных систем и программирования, ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар;
Ключко В.И., д.т.н., профессор кафедры информационных систем и программирования, ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар.
Работа поступила в редакцию 04.06.2014.



