Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Глобоидные червячные передачи по сравнению с цилиндрическими червячными передачами имеют преимущества как по нагрузочной способности и коэффициенту полезного действия, так и по массогабаритным характеристикам [1, 2]. Уменьшение массы глобоидного редуктора может быть в 5–8 раз по сравнению с цилиндрическим редуктором, передающим одинаковую нагрузку [3]. В связи с отмеченным глобоидные передачи применяются в механизмах техники оборонного и специального назначения [1].

Однако традиционная технология изготовления деталей глобоидных пар в настоящее время является трудоемкой. Наиболее сложным является конструктивное исполнение режущего инструмента для обработки винтовой поверхности глобоидного червяка. Диаметральные размеры его совпадают с диаметральными размерами сопряженного червячного колеса глобоидной пары и определяются по формуле

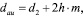(1)

где d_au – наружный диаметр сборного режущего инструмента, мм; d₂ – диаметр делительной окружности червячного колеса, мм; h – коэффициент высоты делительной ножки витка червяка.

Кроме того, изготовление деталей глобоидной передачи по известной технологии обладает низкой производительностью и высокой трудоемкостью, в том числе при сборке. В связи с этим необходимо изыскание более рациональной технологии изготовления деталей глобоидной пары.

Одним из эффективных путей решения этой задачи является применение технологии ротационного точения винтовой поверхности глобоидного червяка принудительно вращаемым многолезвийным инструментом с эвольвентным профилем [4].

Использование ротационного точения позволяет рационализировать конструкцию технологического оборудования для обработки винтовой поверхности глобоидного червяка за счет исключения из кинематической цепи делительной червячной пары. Это существенно уменьшает его габаритомассовые характеристики, а также скажется на увеличении крутильной жесткости кинематической цепи. В зависимости от типа производства это могут быть устройства для ротационного точения винтовой поверхности на бездифференциальной основе, интегрированные с токарно-винторезными станками [5, 6], или сугубо специальные станки с более рациональной кинематической и компоновочной схемами.

С целью подтверждения выдвинутой гипотезы о возможности применения ротационного точения винтовой поверхности глобоидного червяка многолезвийным инструментом с эвольвентным профилем разработана модель и выполнен численный эксперимент по формированию профиля винтовой поверхности глобоидного червяка данным способом.

Схема элементарных движений при формообразовании винтовой поверхности глобоидного червяка ротационным точением принудительно вращаемым многолезвийным инструментом показана на рис. 1.

Математическая модель формирования профиля винтовой поверхности глобоидного червяка включает в себя следующий алгоритм вычислений.

1. Расчет геометрических параметров многолезвийного инструмента, включающий расчет минимально допустимого числа режущих элементов инструмента, позволяющих избежать явления подреза профиля червяка при его формировании [7].
2. Расчет координат профиля многолезвийного инструмента.
3. Расчет числа резов при формировании профиля винтовой поверхности глобоидного червяка ротационным точением в зависимости от продольной подачи инструмента.
4. Расчет координат последовательного положения базовых точек, расположенных на профиле режущего инструмента.
5. Расчет максимальной толщины срезаемого слоя припуска вершиной режущего элемента инструмента в зависимости от продольной подачи инструмента и порядкового номера реза в проекции на ось y.

При разработке математической модели формообразования профиля винтовой поверхности глобоидного червяка необходимо иметь в аналитической форме выражения для координат профиля режущего элемента инструмента как для эвольвентного участка, так и его нерабочей переходной части.

В нашем исследовании для расчета профиля режущих элементов инструмента мы воспользовались прямоугольной системой координат, при которой ось у расположена симметрично относительно профиля режущего элемента и с началом координат на окружности впадин, а также вспомогательной системой координат x₀o_uy₀ с осью y₀, проходящей через точку III пересечения профиля инструмента с делительной окружностью, и с началом координат в 0_u – центре инструмента. Делительная окружность совпадает с центроидой инструмента. При этом также использовались математические выражения, приведенные в работе [8]. Схема расположения прямоугольной системы координат относительно профиля режущего элемента представлена на рис. 2.

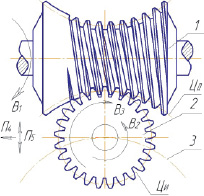
Рис. 1. Схема распределения элементарных движений при формообразовании винтовой поверхности глобоидного червяка ротационным точением принудительно вращаемым многолезвийным инструментом: 1 – заготовка глобоидного червяка; 2 – многолезвийный инструмент; 3 – траектория движения оси инструмента, эквидистантная Ц_Д, Ц_Д – центроида глобоидного червяка, Ц_И – центроида многолезвийного инструмента; B₁ – движение червяка в форме вращения; В₂ и В₃ – движения инструмента в форме вращения, суммируемые на его оси; П₄ – движение инструмента вдоль оси детали в поступательной форме; П₅ – движение инструмента в направлении, перпендикулярном к продольной оси детали

Уравнение эвольвенты профиля режущего элемента в принятой системе координат имеет вид (2) [8]:

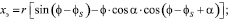
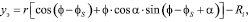(2)

где φ – текущий параметр, соответствующий углу обкатки при нарезании зубьев многолезвийного инструмента червячной фрезой. Значение текущего параметра φ для фиксирующих точек II, III и IV эвольвентной части профиля (рис. 2) определяется из выражения вида (3) [8]:

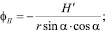
ϕIII = 0; (3)

ϕIV = –tg α,

где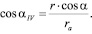

Это позволяет получить с учетом указанных зависимостей выражение для интервала изменения текущего параметра φ вида

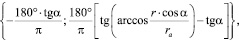(4)

где φ_s – половина угловой толщины зуба инструмента, определяемая из выражения вида

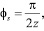(5)

где z – число зубьев инструмента.

Уравнения переходной части профиля режущего элемента в принятой системе координат (рис. 2) имеет вид (6) [7]:

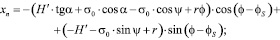(6)

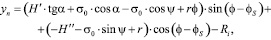
где 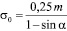– значение текущего параметра φ для точки Ι переходной части профиля зуба режущего элемента в принятой системе координат (рис. 2) имеет вид 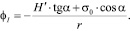(7):

(7)

С учетом зависимостей для текущего параметра в фиксированных точках Ι и ΙΙ профиля получено выражение для изменения текущего параметра φ при формировании переходной части профиля вида

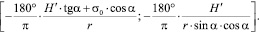(8)

Расчет значений текущего параметра φ в зависимости от продольной подачи S многолезвийного инструмента и порядкового номера i координат последовательного положения базовых точек на режущем элементе инструмента (порядкового номера реза) выполняется по зависимости вида

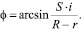(9)

Из анализа схемы движений (рис. 1) при формообразовании винтовой поверхности глобоидного червяка ротационным точением следует, что если одно из звеньев глобоидной пары (червяк) считать неподвижным, то центроида инструмента в форме окружности перекатывается без скольжения по неподвижной центроиде детали. В этом случае, траектория точек, лежащих на центроиде инструмента, а также точек, лежащих вне центроиды, но жестко связанных с ней, могут быть описаны уравнениями гипоциклоидальных кривых. Поэтому руководствуясь методикой определения сопряженных профилей по двум фиксирующим точкам [9], выбираем одну базовую точку A на режущем элементе, на пересечении его оси симметрии с центроидой инструмента, а вторую B – с окружностью выступов, и рассчитываем координаты их последовательного положения в зависимости от продольной подачи и порядкового номера реза по уравнениям гипоциклоидальных кривых.

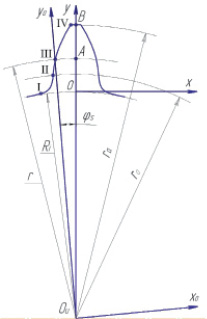
Рис. 2. Схема расположения прямоугольной системы координат xoy и x0ouy0 относительно профиля режущего элемента: I, II, III и IV точки на эвольвентной и переходной частях профиля; Ri – радиус окружности впадин инструмента; ra – радиус окружности выступов инструмента; r – радиус центроиды инструмента; φs – половина угловой толщины зуба инструмента на окружности, совпадающая с центроидой радиуса r

Траектории движения базовых точек А и В описываются уравнениями нормальной (10) и удлиненной (11) гипоциклоидой соответственно:

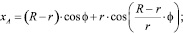(10)

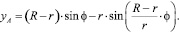
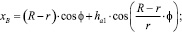(11)

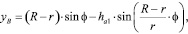
где ha1 – высота делительной головки глобоидного червяка.

Расчет максимальной толщины срезаемого слоя припуска при формировании профиля винтовой поверхности глобоидного червяка вершиной режущего элемента многолезвийного инструмента в зависимости от продольной подачи инструмента и порядкового номера реза в проекции на ось y выполняется по зависимости

(12)

где y_bi и y_bi–1 – координаты базовой точки B на двух последовательных резах.

Разработанная математическая модель позволяет осуществлять проведение численного эксперимента по исследованию процесса формирования винтовой поверхности глобоидного червяка ротационным точением.

Представление о характере изменения и форме срезаемого припуска, а также о загрузке режущих кромок инструмента необходимы для выбора рациональной подачи и оценки эффективности процесса ротационного точения в целом.

На рис. 3 представлены результаты численного эксперимента, выполненного в среде MATLAB согласно разработанному алгоритму.

Оценку производительности срезания припуска при черновой обработке винтовой поверхности глобоидного червяка ротационным точением принудительно вращаемым многолезвийным инструментом выполняли путем сравнения основного времени ротационного точения с основным временем обработки трехрезцовой головкой по существующей технологии применительно к обработке винтовой поверхности глобоидного червяка модулем 10 мм, для глобоидной передачи с характеристикой: модуль 10 мм, межосевое расстояние 500 мм, передаточное отношение 80, число зубьев червячного колеса 80.

При определении численного значения машинного времени при ротационном точении величину подачи принимали равной S = 1,5 мм/об, число проходов при срезании припуска принимали i = 6, число оборотов шпинделя при срезании припуска принимали равным n = 30 об/мин (число оборотов определяется с учетом скорости резания 20–35 м/мин), число оборотов шпинделя при обратных ходах принимали равным n = 66 об/мин. Значение режимов резания было принято с учетом данных работы [10] и результатов численного эксперимента (рис. 3). При этом машинное время обработки на черновой операции составило 81 мин.

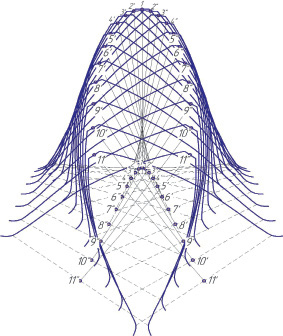
Рис. 3. Модель срезания припуска при формировании профиля винтовой поверхности глобоидного червяка ротационным точением многолезвийным инструментом: 11′–11′…2′–2′ положение профиля режущего элемента инструмента при входе, 1–1 верхнее положение профиля режущего элемента, 2′′–2′′…11′′–11′′ положение режущего элемента инструмента при выходе из впадины профиля глобоидного червяка

Расчет основного времени обработки по существующей технологии методом радиальной подачи выполнены по формуле вида [11]

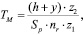(13)

где S_p – радиальная подача, мм; h – высота зуба нарезаемого червяка; z₁ – число заходов червяка; z₂ – число зубьев червячного колеса глобоидной передачи; y – величина врезания, мм; n_r – число оборотов червяка, мин.

Режимы были выбраны по данным работы [12]. При этом машинное время обработки винтовой поверхности глобоидного червяка на черновой операции составило 307 мин.

В результате исследования процесса формирования профиля винтовой поверхности глобоидного червяка на основе численного эксперимента установлено следующее:

1. Срезаемый слой припуска имеет сложную форму при переменной толщине как в пределах одного реза, так и от реза к резу.
2. Вследствие сложной формы срезаемого слоя имеет место несвободное резание.
3. Основная масса припуска срезатся вершиной и входной боковой стороной режущей кромки зуба инструмента.
4. Максимальную толщину имеет срезаемый слой вершиной режущего элемента инструмента.
5. Толщина срезаемого слоя припуска, снимаемого различными участками режущей кромки инструмента, имеет большие значения в начале удаления припуска из впадины витка и меньшие в конце формирования впадины.
6. Обработку ротационным точением винтовой поверхности глобоидного червяка можно осуществлять при продольной подаче инструмента до 2 мм на оборот. При этом толщина срезаемого слоя вершиной режущего элемента на первых резах не превышает 0,5 мм, что вполне приемлемо из условия обеспечения работоспособности режущей кромки.
7. Повышение производительности процесса на черновой операции может составлять до 3,8 раз, по сравнению с обработкой трехрезцовой головкой по существующему варианту технологии. При этом процесс является многопроходным. Глубина резания на первых проходах составляет 3 мм с увеличением на последующих до 6 мм.

Анализ полученных результатов расчета показывает, что применение ротационного точения обеспечивает повышение производительности процесса обработки по машинному времени в сравнении с применяемой в настоящее время обработкой трехрезцовой головкой в 3,8 раза. Полученные результаты исследования процесса формирования профиля глобоидного червяка на основе численного эксперимента имеют важное значение для подтверждения вывода о том, что применение ротационного точения является одним из эффективных направлений совершенствования технологии обработки червячной пары глобоидной передачи.

Рецензенты:

Ереско Т.Т., д.т.н., профессор, заведующий кафедрой «Основы конструирования машин», ФГБОУ ВПО «Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева», г. Красноярск;

Беляев С.В., д.т.н., профессор, заведующий кафедрой литейного производства, ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.

Работа поступила в редакцию 04.06.2014.