Идеи повышения эксплуатационной надежности оснований современных зданий и сооружений начали находить возможности своего приложения в практику проектирования достаточно давно. Одно из направлений – увеличение несущей способности грунтового основания за счет армирования грунта. Сама идея об использовании различных разновидностей вертикального и горизонтального армирования слабого грунтового основания в принципе была известна. Так, имели определенное распространение методы глубинной стабилизации слабых грунтов цементными и цементнопесчаными растворами [1, 5, 6]. Увеличение несущей способности горизонтальным армированием основания предложено французcкими учеными J. Binguet, K. Lee [7]. Авторами [7] показано, что горизонтальное армирование основания при трех слоях армирования синтетическими материалами в 1,6 раза увеличило несущую способность основания. Исследования горизонтально армированных оснований проводились также в университете штата Сан-Диего. Авторами было доказано, что несущая способность горизонтально армированного песчаного основания в зависимости от его плотности увеличивается от 1,2 до 1,6 раз. Перечисленные выше сведения об армировании грунтового основания можно отнести к «пассивным» системам повышения несущей способности оснований. В работах [2, 3] ставится вопрос об «активных» методах управления эксплуатационной надежностью и напряженно-деформированным состоянием основания. Идея активности методов управления эксплуатационной надежностью строительных конструкций вообще и оснований зданий и сооружений в частности неразрывно связана с теорией автоматического управления, методология которого применительно к регулированию напряженно-деформированного состояния (НДС) строительных конструкций существует только в виде отдельных положений.
В работах Землянского А.А. принцип активности методов управления предлагается осуществлять за счет активного горизонтального армирования грунта с помощью шпунтовой стенки или полых рабочих свай с обеспечением возможности перемещений их боковых поверхностей (рис. 1). Активное армирование основания за счет давления преднапряжения в армирующей системе позволяет, как это экспериментально подтверждено в [2–4], повысить прочность и устойчивость слабых грунтов.
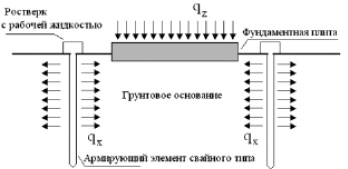
Рис. 1. Схема активного армирования основания
Непосредственной причиной повышения несущей способности грунтового основания, армированного активной горизонтальной системой, является предварительное напряжение грунтовой массы основания под фундаментной плитой. Теоретически учет такого преднапряжения связан с проявлением распределительных свойств грунта. Для этого необходима математическая модель основания, учитывающая полный вектор перемещений (вертикальные и горизонтальные перемещения).
Для выявления особенностей НДС преднапряженного основания использована модель, представленная на рис. 2, а. Данная модель представляет собой грунтовый массив, ограниченный с двух сторон достаточно протяженными по длине армирующими элементами, создающими кинематическое нагружение. Эти условия позволяют перейти от решения трехмерной задачи к решению плоской симметричной задачи и сократить тем самым количество вычислений.
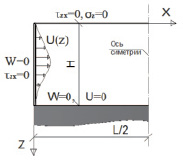 а
а
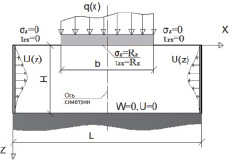 б
б
Рис. 2. Расчетная схема преднапряженного основания: а – при отсутствии вертикальной нагрузки; б – при наличии нагруженной фундаментной плиты
Рассматривая грунтовый массив как линейно деформируемую среду, в качестве неизвестных приняты вертикальные и горизонтальные компоненты (W(x, z), U(x, z)) вектора перемещений. В этом случае разрешающими уравнениями являются уравнения Ляме для плоской задачи:
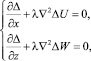 (1)
(1)
где 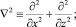
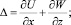
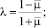
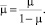
Расчетная схема преднапряженного основания без вертикального давления с граничными значениями перемещений и напряжений представлена на рис. 2. Для дискретизации этой модели в области интегрирования использован метод конечных разностей. В качестве исходных данных приняты следующие параметры: H = 10 м, L = 40 м, Егр = 20000 кПа, ν = 0,5, где H и L – размеры области интегрирования; Егр – модуль деформации грунта; ν – коэффициент Пуассона.
Предварительное напряжение грунта в данном случае задается в виде функции кинематического перемещения стенок армирующего элемента
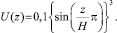
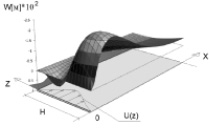
Эпюры перемещений основания W(x, z), U(x, z) представлены на рис. 3.
 а
а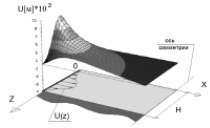 б
б
Рис. 3. Эпюры перемещений слоя основания: а – вертикальных (W); б – горизонтальных (U)
На рис. 3, а можно наблюдать вертикальный выпор грунта вблизи зоны кинематического нагружения, убывающий по глубине слоя основания. Этот эффект обуславливает снижение осадок фундаментной конструкции при вертикальной нагрузке на армированный массив. В связи с принятой формой эпюры нагружения U(z) значения вертикальных перемещений вдоль оси Z приобретают обратный знак. Горизонтальные перемещения затухают ближе к оси симметрии (рис. 3, б).
НДС преднапряженного основания напрямую зависит от условий взаимодействия армирующего элемента с грунтовым массивом. Эпюры на рис. 3 соответствуют граничному условию, предполагающему отсутствие вертикальных перемещений грунта по поверхности армирующего элемента (Wгр = 0). При условии отсутствия касательных напряжений на границе армирования (τгр = 0), предполагающем свободное перемещение грунта по армирующему элементу, картина распределения перемещений грунтового массива качественно изменяется. Для наглядности сравним перемещения поверхности армированного основания с различными граничными условиями (рис. 4). Функция кинематического перемещения по высоте слоя при этом принята постоянной (U(z) = 0,2 м). Как видно из графиков на рис. 4, а, при условии (τгр = 0) максимальные вертикальные перемещения поверхности основания W(x) концентрируются у границы активного армирования. При условии (Wгр = 0) максимальный выпор грунта находится на некотором удалении от этой границы.
Условию (τгр = 0) соответствует большее абсолютное значение вертикальных перемещений. Также видно, что независимо от граничных условий вертикальные перемещения поверхности основания затухают по мере удаления от границы основания, взаимодействующей со шпунтом. То же происходит и с горизонтальными перемещениями U(x) (рис. 4, б).
При рассмотрении системы «фундаментная плита – преднапряженное основание», помимо граничных условий в постановке задачи, на НДС системы также существенное влияние оказывает положение армирующего элемента относительно фундаментной плиты и по высоте слоя основания. Попробуем проследить влияние рассмотренных различий в постановке задачи на НДС системы «фундаментная плита – преднапряженное основание». Для выявления особенностей НДС грунтового массива при сложном напряженном состоянии использована модель, представленная на рис. 2, б. В отличие от предыдущей модели, на рассматриваемый преднапряженный объем грунта опирается плита с соотношением сторон l/b > 10 нагруженная равномерно распределенной нагрузкой. Считается, что поверхность контакта балки и основания является абсолютно гладкой, а реакции контакта направлены по нормали к этой поверхности. Также предполагается, что вертикальные перемещения поверхности основания и нижней поверхности балки происходят совместно без отрыва, и величина вертикального давления, передаваемого на поверхность основания со стороны балки, равна вертикальному отпору Rz(x). Вертикальный отпор связан условием равновесия балки с величиной ее изгибной жесткости (EJ) и характером нагрузки q(x):
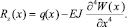 (2)
(2)
 а
а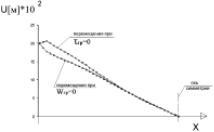 б
б
Рис. 4. Эпюры перемещений поверхности основания: а – вертикальных – W(x); б – горизонтальных – U(x)
Решение задачи находится на основе совместного решения системы уравнений Ляме (1) с уравнением изгиба балки (2), входящим в систему уравнений через граничные условия, записанные для участка поверхности основания, контактирующего с балкой.
На рис. 5 представлены эпюры вертикальных перемещений поверхности основания W(x) при различных граничных условиях контакта грунта с армирующим элементом.
Для исходных данных приняты следующие параметры: H = 30 м, L = 40 м, Егр = 20000 кПа, Еb = 21000000 кПа, ν = 0,5, hb = 1 м, q(x) = 500 кН/м, L/b = 1,5.
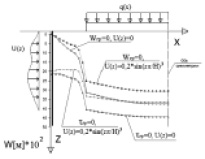
Рис. 5. Перемещения поверхности основания W(x) под фундаментной плитой
Как видно из графиков (рис. 5), кинематическое нагружение грунта способствует снижению вертикальных осадок фундаментной плиты на 18 %. Наибольший эффект наблюдается при отсутствии вертикальных перемещений грунта по поверхности армирующего элемента (Wгр = 0). Отсутствие касательных напряжений (τгр = 0) в данном случае ухудшает работу грунтового массива и увеличивает осадки на 20 %.
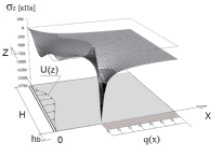
Оценивая снижение осадок фундаментной плиты, следует принимать во внимание упругую работу грунта под нагрузкой. В рассматриваемой линейной постановке задачи снижение осадок плиты прямо пропорционально увеличению величины кинематического нагружения. Особенности данной математической модели также можно отметить на эпюрах распределения напряжений в основании. Качественная картина распределения нормальных и касательных напряжений σz и τzx для системы «фундаментная плита – преднапряженное основание» представлена на рис. 6.
 а
а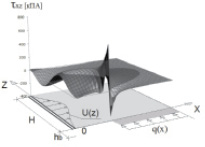 б
б
Рис. 6. Эпюры напряжений слоя основания: а – нормальных (σz); б – касательных (τzx)
Вдоль поверхности армирующего элемента присутствуют характерные очертания эпюр нормальных и касательных напряжений, обусловленные кинематическим нагружением (рис. 6). Максимальная же концентрация напряжений находится под торцом балки. Напряжения в этом месте возрастают по мере сгущения конечно-разностной сетки. При таких значениях напряжений в грунте, как правило, происходит развитие зон предельного равновесия, и грунт переходит в пластическую стадию работы. Для данной модели это обстоятельство накладывает соответствующие ограничения на величину вертикальной нагрузки.
При анализе величины абсолютных осадок фундаментной плиты следует учесть влияние положения армирующего элемента относительно фундаментной плиты и по глубине слоя основания. По мере смещения армирующего элемента к краю плиты наблюдается снижение ее осадок. Вместе с тем усиливается и влияние рассмотренных краевых эффектов.
Таким образом, напряженно-деформируемое состояние системы «фундаментная плита – преднапряженное основание» определяется многими факторами. Использование приведенной математической модели в рамках упругой задачи позволяет выделить наиболее существенные из них для более точной оценки НДС основания с активным армированием. В частности, при формулировке граничных условий необходимым является учет сил трения между грунтом и армирующим элементом, отражающий характер их взаимодействия. Также необходимым является учет неупругих свойств грунтовой среды. Для данной модели линейно-деформированного основания при активном армировании наблюдается снижение осадок фундаментной плиты под нагрузкой пропорционально увеличению величины кинематического нагружения, что дает повод для дальнейшего изучения вопросов математического моделирования, прочности и устойчивости преднапряженных оснований и их совместной работы с сооружениями.
Рецензенты:
Денисова А.П., д.т.н., профессор, Саратовский государственный технический университет имени Гагарина Ю.А., г. Саратов;
Гарибов Р.Б., д.т.н., генеральный директор, ЗАО «Научно-технический центр «Волгапромстройбезопасность», г. Энгельс.
Работа поступила в редакцию 04.06.2014.



