Решение задачи о движении тяжелого твердого тела вокруг неподвижной точки представляет собой одну из интереснейших задач динамики твёрдого тела. На сегодняшний день имеются значительные результаты, полученные при ее решении в течение более двух столетий. Связывая между собой определенным образом осевые моменты инерции, Л. Эйлер, Ж. Лагранж, С.В. Ковалевская нашли четвертый интеграл системы дифференциальных уравнений движения тела. В дальнейшем работы велись в направлении определения решений для случаев, когда накладывались некоторые ограничения на начальные условия задачи (случаи В. Гесса – Г.Г. Аппельрота, Д.Н. Горячева – С.А. Чаплыгина, Д.К. Бобылева – В.А. Стеклова и другие).
В данной работе приведено частное решение уравнений движения симметричного твердого тела переменной массы с закрепленной точкой, на которое действует дополнительная сила переменного направления, параллельного линии, лежащей в неподвижной горизонтальной плоскости перпендикулярно линии узлов. Предполагается:
- относительные скорости отбрасываемых частиц равны нулю;
- главные оси инерции тела для неподвижной точки относительно твёрдого тела не перемещаются;
- в рассматриваемом промежутке времени между главными моментами инерции тела выполняется соотношение 2А = В (случай аналогичен случаю Д.К. Бобылева – В.А. Стеклова). Кроме того, во всё время движения центр масс твёрдого тела находится на оси «y» в экваториальной плоскости эллипсоида инерции, так что координаты центра масс тела
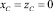 , а точка приложения дополнительной силы
, а точка приложения дополнительной силы 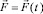 – в экваториальной плоскости эллипсоида инерции перпендикулярно линии узлов (точка приложения силы перемещается во всё время движения относительно твёрдого тела).
– в экваториальной плоскости эллипсоида инерции перпендикулярно линии узлов (точка приложения силы перемещается во всё время движения относительно твёрдого тела).
Дифференциальные уравнения движения тяжелого твердого тела переменной массы (динамические уравнения Эйлера) с закрепленной точкой в общем случае, если момент реактивных сил равен нулю, согласно [1, 2, 3], имеют вид
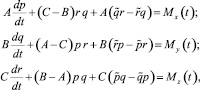 (1)
(1)
где x, y, z – подвижные оси, неизменно связанные с телом; p, q, r – проекции вектора угловой скорости вращения тела на оси подвижной системы координат, совпадающие в каждый момент времени с главными осями эллипсоида инерции, построенного для неподвижной точки О; 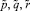 – проекции вектора угловой скорости вращения на оси, совпадающие с главными осями эллипсоида инерции для неподвижной точки.
– проекции вектора угловой скорости вращения на оси, совпадающие с главными осями эллипсоида инерции для неподвижной точки.
Динамические уравнения Эйлера для рассматриваемого твёрдого тела примут вид [4]
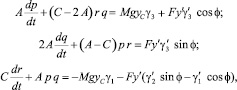 (2)
(2)
где
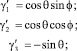 – направляющие косинусы силы
– направляющие косинусы силы 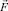 переменного направления; γ1, γ2, γ3 – направляющие косинусы силы тяжести; y′ – алгебраическое значение радиус-вектора точки приложения силы.
переменного направления; γ1, γ2, γ3 – направляющие косинусы силы тяжести; y′ – алгебраическое значение радиус-вектора точки приложения силы.
Таким образом, динамические уравнения Эйлера можно представить следующим образом [3, 5]:
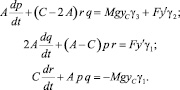 (3)
(3)
Для решения задачи к динамическим уравнениям Эйлера присоединяем кинематические уравнения
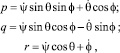 (4)
(4)
или уравнения Пуассона
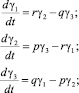 (5)
(5)
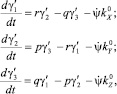 (6)
(6)
где 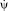 – алгебраическое значение угловой скорости прецессии;
– алгебраическое значение угловой скорости прецессии; 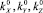 – проекции единичного вектора линии узлов на оси подвижной системы координат.
– проекции единичного вектора линии узлов на оси подвижной системы координат.
В случае движения тяжёлого твёрдого тела переменной массы под действием силы переменного направления для получения интеграла энергии введем следующие ограничения:
 (7)
(7)
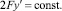 (8)
(8)
Интеграл энергии при условиях (7), (8) примет вид
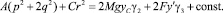 (9)
(9)
Тривиальный интеграл запишем в виде:
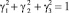
или
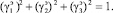 (10)
(10)
Из теоремы об изменении кинетического момента получаем ещё один первый интеграл
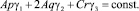 (11)
(11)
Последний первый интеграл в общем случае получить не удаётся.
Для исследования устойчивости движения твёрдого тела запишем частное решение системы (3), (5) в виде [2]:
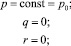
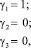 (12)
(12)
положив
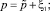
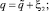
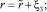
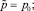
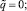
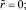 (13)
(13)
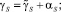
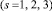
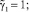
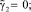
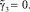
Используя метод интегральных связок Четаева, интегралы (9), (10), (11) запишем в виде:
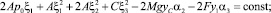
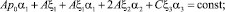 (14)
(14)
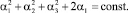
Следовательно, связку интегралов в общем виде можно представить:
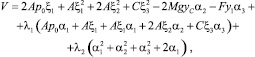 (15)
(15)
где λ1, λ2 – произвольные постоянные, которые следует соответствующим образом выбрать.
Для исключения линейных членов необходимо выполнение равенств
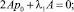 (16)
(16)
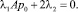 (17)
(17)
Таким образом,
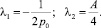 (18)
(18)
После преобразований связка интегралов примет вид
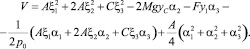 (19)
(19)
Разобьём функцию V на три функции
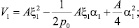 (20)
(20)
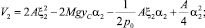 (21)
(21)
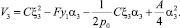 (22)
(22)
Далее необходимо добиться определённо-положительности этих трёх форм. Запишем условие Сильвестра для функции V1
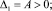
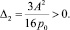 (23)
(23)
Таким образом, функция V1 > 0, следовательно, устойчивость параметров p и γ1 доказана.
Условие положительности форм V2 и V3 заключается в выполнении неравенств
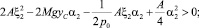 (24)
(24)
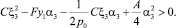 (25)
(25)
Неравенства (24) и (25) выполняются при условиях:
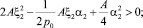
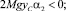 (26)
(26)
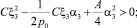
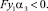 (27)
(27)
Вторые равенства в (26) и (27) могут быть обеспечены выбором yC и y1.
Условия положительности первых форм этих же равенств обеспечивают условия Сильвестра, которые для (26) имеют вид:
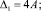
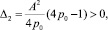 (28)
(28)
для (27):
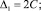
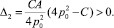 (29)
(29)
Итак, выполнение условий (26), (27) и (28), (29) является достаточным для устойчивости по переменным q, r, γ2, γ3.
Рецензенты:
Денисов В.Н., д.т.н., доцент, кафедра «Высшая математика», Смоленский филиал национального исследовательского университета «МЭИ», г. Смоленск;
Омаров Т.И., д.т.н., доцент, кафедра «Прикладная механика и основы конструирования машин» Казахский национальный технический университет, г. Алматы.
Работа поступила в редакцию 15.05.2014.



