В 2011–2012 годах разработаны узловые соединения сетчатых куполов со стержнями из тонкостенных холодногнутых профилей [2, 3] и проведено численное и экспериментальное исследование их напряженно-деформированного состояния [5].
В ходе исследований было выявлено, что узловые соединения обладают некоторой податливостью. Податливость узловых соединений купола оказывает влияние на напряженно-деформированное состояние купола, в том числе на усилия в стержнях и прогибы узлов. Целью настоящей работы является определение степени влияния податливости узловых соединений купола на его напряженно-деформированное состояние.
Материалы и методы исследования
Оценка влияния податливости узловых соединений купола выполнялась с использованием программного комплекса «Лира 9.4» с моделированием податливости узловых соединений тремя способами:
1. Произвести пересчет модуля упругости стержневых элементов с учетом податливости узловых соединений. Данный метод используется в работах О.Ю. Дериглазова и И.С. Инжутова [1].
2. Установить на концы стержней упругие элементы, податливость которых будет равна податливости узловых соединений купола.
3. Заменой в расчетной схеме купола цилиндрического элемента узлового соединения шестиугольником из шести прямых стержней соответствующей длины, жестко соединенных между собой и вписанных в круг с радиусом, равным радиусу цилиндрического элемента.
Исследование податливости узловых соединений купола выполним на примере сетчатого купола диаметром 12 метров с тремя ярусами стержней всеми тремя описанными способами. Методика построения расчетной схемы купола, нагрузки и закрепления аналогичны описанным в работах [4, 6].
Пересчет модуля упругости осуществляется по формуле
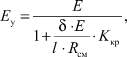 (1)
(1)
где Е – реальный модуль упругости материала стержней купола (2·105 МПа); δ – возможное предельное значение деформаций податливости (принимаем равным толщине цилиндрического элемента узла, т.е. 3 мм); l – длина стержня купола (2,5 метра); Rсм – расчетное сопротивление местному смятию (173 МПа); Kкр – коэффициент, учитывающий длительность действия нагрузки, для длительной и постоянной нагрузки Kкр = 1.
Подставляя в формулу, получаем условный модуль упругости Еу = 8,53·104 МПа.
Условный модуль упругости используем только для материала тонкостенных стержней каркаса купола, для стержней нижнего опорного кольца купола применяем реальный модуль упругости материала, так как узлы нижнего опорного кольца можно считать абсолютно жесткими.
Во втором способе для учета податливости узловых соединений на концы стержней купола устанавливаются и жестко соединяются упругие элементы с длиной равной радиусу цилиндра узлового соединения. Вид фрагмента расчетной схемы купола с установленными упругими элементами показан на рис. 1.
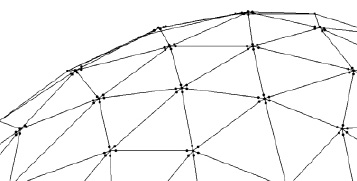
Рис. 1. Фрагмент расчетной схемы купола с установленными упругими элементами
Из численного исследования узлового соединения диаметром 300 мм, высотой 150 мм и толщиной 3 мм [5] было выявлено, что в пределах линейной работы узлового соединения прогиб стенки цилиндра узлового соединения также практически линеен. Так, например, при нагрузке 9,6 кН прогиб стенки цилиндра составил 0,223 мм. Следовательно, для обеспечения равной податливости при данной нагрузке продольные деформации устанавливаемых на концы стержней упругих элементов должны также быть равными 0,223 мм.
Зависимость деформаций от прилагаемой силы описывается формулой
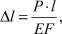 (2)
(2)
где Е – модуль упругости элемента; F – площадь поперечного сечения элемента; P – приложенная сила; l – длина элемента; Δl – продольные деформации элемента.
Так как для задания жесткости стержневого элемента в ПК Лира достаточно задать его EF, то вычислим это значение:
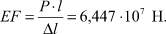
В третьем способе узловые соединения были представлены в виде шестиугольников, вписанных в круг радиусом 150 мм, как показано на рис. 2. Сечение стержней шестиугольников выполнено в виде швеллера высотой 150 мм, ширина полки 15 мм, толщина стенки и полок по 3 мм, т.е. в соответствии с реальными размерами узлового соединения.
Результаты исследования и их обсуждение
Результаты сравнительных расчетов купола с учетом податливости узловых соединений различными способами представлены в табл. 1 и 2. Все данные приведены при загружении купола равномерной снеговой нагрузкой 240 кг/м2 по всей поверх- ности купола.
Как можно заметить из табл. 1, учет податливости путем пересчета модуля упругости стержневых элементов купола практически не вызывает изменений усилий в стержнях купола, а другими методами показывает снижение максимальных усилий на 12–15 %. В целом снижение усилий в стержнях купола достаточно равномерное и пропорционально снижению максимальных усилий, т.е. составляет 12–15 %.
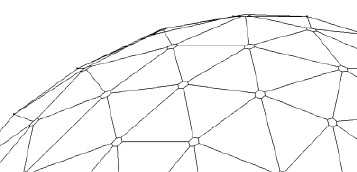
Рис. 2. Фрагмент расчетной схемы купола с установленными узловыми соединениями в виде шестиугольников
Таблица 1
Влияние податливости на усилия в стержнях купола
|
Максимальное усилие в тонкостенных стержнях каркаса купола, кН |
Разница со стандартной расчетной схемой без учета податливости, % |
Максимальное усилие в стержнях нижнего опорного кольца купола, кН |
Разница со стандартной расчетной схемой без учета податливости, % |
|
|
Без учета податливости |
14,1 |
– |
3,28 |
– |
|
Учет податливости путем изменения модуля упругости узловых соединений |
13,9 |
1,42 |
3,28 |
0 |
|
Учет податливости путем установки упругих элементов на окончания стержней купола |
12,1 |
14,2 |
2,82 |
14,0 |
|
Учет податливости путем моделирования узловых соединений в виде шестиугольников |
12,3 |
12,8 |
2,99 |
8,84 |
Таблица 2
Влияние податливости на деформацию купола
|
Прогиб центрального узла купола, мм |
Разница со стандартной расчетной схемой без учета податливости, % |
|
|
Без учета податливости |
2,75 |
– |
|
Учет податливости путем изменения модуля упругости узловых соединений |
3,83 |
39,3 |
|
Учет податливости путем установки упругих элементов на окончания стержней купола |
4,39 |
59,6 |
|
Учет податливости путем моделирования узловых соединений в виде шестиугольников |
3,48 |
26,5 |
Анализируя табл. 2, можно сделать вы- вод, что учет податливости узловых соединений любым из методов показывает увеличение деформативности конструк- ции в целом.
Выводы
По результатам исследования можно сделать следующие выводы о влиянии податливости узловых соединений купола на его напряженно-деформированное состояние:
- Учет податливости приводит к уменьшению усилий в стержнях купола на величину до 15 %.
- Деформативность купола значительно увеличивается.
- Для практических расчетов возможно использовать расчетные схемы куполов без учета податливости узловых соединений, так как несколько завышенные усилия в стержнях купола пойдут в запас прочности. Тем не менее при расчете по схеме без учета податливости следует учитывать повышенную деформативность конструкции при выборе конструктивного решения кровли купола.
Рецензенты:
Шарапов В.И., д.т.н., профессор, заведующий кафедрой «Теплогазоснабжение и вентиляция» Ульяновского государственного технического университета, г. Ульяновск;
Манжосов В.К., д.т.н., профессор, заведующий кафедрой «Теоретическая и прикладная механика» Ульяновского государственного технического университета, г. Ульяновск.
Работа поступила в редакцию 30.04.2014.



