Существует довольно много методов решения линейных дифференциальных уравнений (см., например, [2]). Наиболее распространенным методом является поиск общего решения в виде суммы общего решения однородной части данного линейного уравнения и частного решения, подбираемого по виду неоднородности [4]. Каждый вид неоднородности предполагает собственный вид частного решения, которое, как правило, ищется методом неопределенных коэффициентов. Поскольку вид частного решения зависит от вида неоднородности и не всегда может быть выражен в общем виде, его поиск часто представляет собой самостоятельную задачу и может потребовать специальных ухищрений. Однако существует метод, позволяющий найти общее решение линейного дифференциального уравнения непосредственным интегрированием без разложения уравнения на однородную и неоднородную части, применение которого наиболее удобно при решении задач теории колебаний [1]. Решение ищется специальным приемом, сочетающим метод неопределенных коэффициентов с интегрированием. Модифицируя метод, изложенный в [1], будем искать общее решение неоднородного уравнения так:
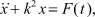(1)
где k = const; F(t) – произвольная функция времени t, в виде
x = Acos kt, (2)
здесь A – искомая переменная функция.
Продифференцировав по времени выражение (2), получим
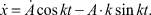(3)
Подставив в уравнение (3) начальные условия x = x0,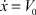 
при t = 0, запишем соответствующие начальные условия для новой переменной A(t) следующим образом:
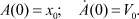(4)
Дифференцируем далее равенство (3) и подставляем полученное выражение в исходное дифференциальное уравнение
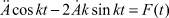. (5)
Если умножить обе части уравнения (5) на cos kt, то можно заметить, что в полученном уравнении
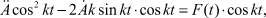(6)
левая часть представляет собой полную производную
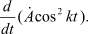(7)
Таким образом, уравнение (6) можно проинтегрировать методом разделения переменных [1], умножив обе его части на dt,
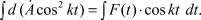(8)
Следовательно,
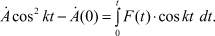(9)
Учитывая второе начальное условие (4), получим
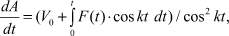(10)
откуда
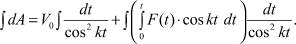(11)
После интегрирования с учетом первого начального условия (4) находим значение искомой функции
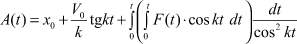(12)
и общее решение уравнения (1) при заданных начальных условиях как
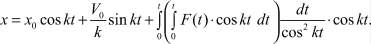(13)
Приведем некоторые ПРИМЕРЫ, демонстрирующие универсальность применяемого метода.
1. При F(t) = 0 уравнение (1) – обычное уравнение свободных гармонических колебаний ‒ имеет вид
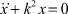, (14)
решение которого известно
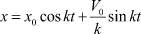. (15)
Очевидно, оно является частным случаем выражения (13).
2. При F(t) = t стандартное решение неоднородного уравнения
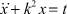(16)
следует искать как сумму общего решения однородного и частного решения, подбираемого по виду правой части
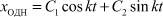, (17)
где C1, C2 – произвольные постоянные;
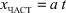, (18)
здесь a – константа, подлежащая определению.
После подстановки частного решения (18) в уравнение (16) получим
k2at = t, (19)
откуда a = 1/k2.
После определения частного решения находим значения произвольных постоянных C1, C2 по заданным начальным условиям. Для этого подставляем их в общее суммарное решение
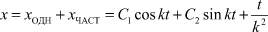(20)
и его производную
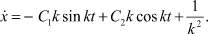(21)
Подставляя t = 0, x = x0,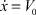 
в уравнения (20) и (21), получим
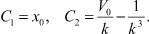(22)
Таким образом,
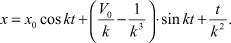(23)
Покажем, что представленное стандартное решение полностью соответствует решению (13). Для этого следует вычислить всего два интеграла
1) 
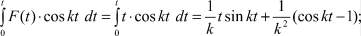(24)
2) 
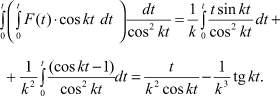(25)
Подставив полученные выражения в (13), убеждаемся, что решение полностью совпадает с соотношением (23).
3. Резонанс.
Вынужденные колебания для случая резонанса рассмотрим на примере уравнения
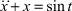(26)
с нулевыми начальными условиями
x =0, V0 = 0. (27)
Для получения частного решения с заданными начальными условиями вычисляем указанные выше два интеграла
1) 
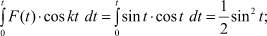(28)
2) 
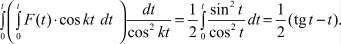(29)
Таким образом,
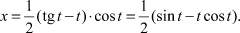(30)
Непосредственной подстановкой можно убедиться в том, что решение (30) удовлетворяет уравнению (26) и нулевым начальным условиям.
Разработанный метод легко распространить на случаи различных законов изменения неоднородности на разных участках. В работе [3] решение уравнения колебаний определялось на каждом участке отдельно и стыковалось граничными условиями: конечные условия предыдущего участка являлись начальными для следующего. Метод прямого интегрирования позволяет объединить все решения в одно.
4. Уравнение с кусочно-непрерывной неоднородностью. Если на разных участках изменения независимой переменной неоднородность представлена разными выражениями, то решение следует проводить аналогично составлению универсального уравнения упругой линии балки в сопротивлении материалов [5]: функцию, заданную на ограниченном участке, следует продолжить до конца промежутка интегрирования, приложив с противоположной стороны симметричную относительно оси абсцисс функцию.
В качестве примера рассмотрим дифференциальное уравнение
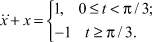(31)
На I участке, где 0 ≤ t < π/3 FI(t) = 1. На II участок, где t ≥ π/3, продлеваем функцию FI(t) = 1, компенсируя ее действие симметричной относительно оси абсцисс функцией –FI(t) = –1. Складывая на участке II –FI(t) и заданное выражение, получим для второго участка FII(t) = –2. Таким образом, неоднородность в уравнении (31), начиная с I участка и до конца промежутка интегрирования представлена функцией FI(t) = 1. Начиная со II участка и до конца промежутка интегрирования F(t) = FI(t) + FII(t) = –2 (от участка к участку количество слагаемых увеличивается). Решаемое дифференциальное уравнение можно записать в виде
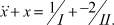(32)
Далее применяем метод прямого интегрирования
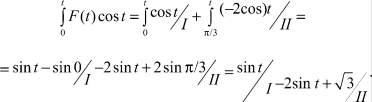(33)
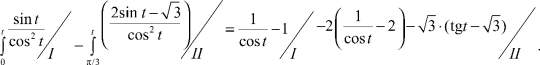(34)
Для t < π/3 решение записываем только по выражению на I-м участке
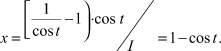(35)
Для t ≥ π/3 общее решение уравнения (31) представляется суммой
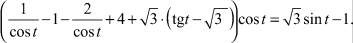(36)
Таким образом, на каждом участке решение получено независимо от остальных.
Рецензенты:
Красовский А.Н., д.ф.-м.н., профессор кафедры графики и деталей машин Уральского государственного аграрного университета, г. Екатеринбург;
Мальцев В.А., д.т.н., профессор, директор института материаловедения и металлургии Уральского федерального университета, г. Екатеринбург.
Работа поступила в редакцию 11.04.2014.